6.3. Способы раскрытия неопределённостей вида и
1.
Если
непосредственная подстановка в дробную
функцию обращает числитель и знаменатель
в нуль, то получаем неопределённость
вида
,
это значит, что предельное значение в
выражение функции можно подставлять
только после предварительного сокращения
данной дроби.
Пример.
=
Для
того чтобы сократить данную дробь,
разложим числитель и знаменатель дроби
на множители по формуле
,
где
и
,
это корни уравнения
.
Получим:
и
.
Тогда исходный предел перепишем в виде :
=
=
= - 9.
2. Рассмотрим предел дроби, в знаменателе которой содержится иррациональная функция. Если при непосредственной подстановки в такую дробь предельного значения числитель и знаменатель обращаются в ноль, то для того чтобы раскрыть полученную неопределённость вида , нужно числитель и знаменатель данной дроби умножить на выражение сопряжённое знаменателю.
Пример.
=
.
Домножим числитель и знаменатель дроби на выражение, сопряженное числителю (избавляемся от иррациональности в числителе):
=
=
=
=
=
=
.
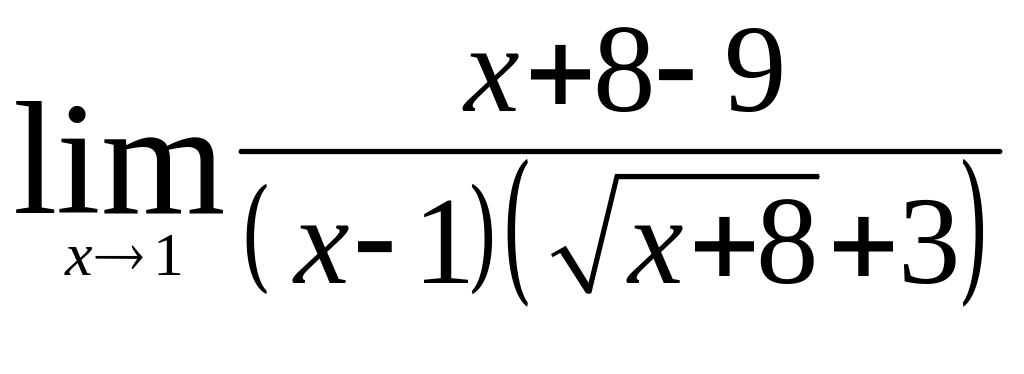В
данном примере выражением, сопряжённым
знаменателю
,
является выражение вида
.
Замечание:
Если делимое
при
,
конечно, а делитель стремится к нулю,
то предел частного не существует и в
этом случае говорят, что этот предел
бесконечен, т.е.
3.
Рассмотрим
частное двух функций
.
Если при
или
,
числитель дроби
и знаменатель дроби
,
то имеем неопределённость вида
.
Пусть в числителе и знаменателе некоторые многочлены. Тогда для раскрытия неопределённости необходимо каждое слагаемое числителя и знаменателя разделить на в наивысшей степени из числа слагаемых числителя и знаменателя, а затем перейти к пределу.
Пример.
=
.
Для
того чтобы, раскрыть неопределенность
вида
надо под знаком предела числитель и
знаменатель дроби разделить на переменную
х с
наивысшим показателем:
=
=
Осталось
воспользоваться теоремами о пределах,
а также тем, что функции
,
и
- бесконечно малые при х
=
=
.
6.4. Первый и второй замечательные пределы
Рассмотрим
предел вида
.
Этот предел называют первым
замечательным пределом
и используется
для раскрытия неопределенностей вида
,
различных функций, содержащих
тригонометрические выражения и степени
.
Пример.
=
.
Домножим
числитель и знаменатель дроби на «3» и
получим
.
Используя теоремы о пределах и первый замечательный предел, получаем:
3
=3.
Рассмотрим
предел функции
.
Если, при
,
функция
,
а функция
,
то говорят, что имеем неопределенность
вида
.
Для раскрытия этой неопределённости
пользуются вторым
замечательным пределом,
который имеет вид
.
Пример.
(1
+
)
В
данном случае неопределенность вида
,
для ее раскрытия сделаем замену у=
.
Тогда
при
и исходный предел сводится ко второму
замечательному пределу:
=
=
=
.
6.5. Непрерывность функции. Точки разрыва
Определение.
Функция
называется
непрерывной в точке
,
если она удовлетворяет следующим трём
требованиям:
определена в точке ;
имеет конечный предел функции при
;этот предел равен значению функции в точке , т.е.
.
Если функция не является непрерывной в точке , то говорят, что в этой точке функция разрывна, а точка называется точкой разрыва функции .
Пределом функции в точке слева (справа), называется предел, вычисляемый в предположение, что , оставаясь всегда меньше (больше) значения . Пределы справа и слева называются односторонними пределами и обозначаются следующим образом:
и
.
Определение.
Точкой
разрыва первого рода называют
точку, в которой существуют конечные
односторонние пределы функции слева и
справа при
,
не равные друг другу, т.е.
Определение. Точкой разрыва второго рода называют точку, в которой хотя бы один из односторонних пределов функции слева и справа при бесконечен или не существует.
Определение. Точкой устранимого разрыва называют точку, в которой существует конечный предел функции, но он не равен значению функции в этой точке.