Контрольный тест после изучения главы 8 «Приложения производной»
1. Сколько точек перегиба имеет функция у = х4 + 4х?
а) ни одной; б) одну; в) две; г) три.
2. Функция у = х3+х …
а) возрастает на ( – ∞; 0), убывает на (0; + ∞);
б) убывает на ( – ∞; 0), возрастает на (0; + ∞);
в) всюду убывает;
г) всюду возрастает.
3. Функция убывает у= х-3-3х на интервале:
а) (3; + ∞); б) ( – ∞; 0)и(0; + ∞); в) ( – ∞; + ∞); г) нигде.
4. Укажите точки экстремума непрерывной на всей числовой прямой функции у(х), если у=(х+1)2(х-2):
а) х = 2 – точка max; б) х = 2 – точка min;
в) х = –1 – точка min; г) точек экстремума нет.
5. Для дифференцируемой функции f(x) из приведенных условий выберите достаточное условие убывания:
6). Для дифференцируемой функции f(x) из приведенных условий выберите достаточное условие выпуклости (выпуклости вверх):
7.
Для дифференцируемой функции f(x)
из приведенных
условий выберите необходимое условие
точки перегиба:
Раздел VI. Функции нескольких переменных
Глава 9. Функция двух переменных
9.1. Основные определения
Определение: Переменная величина z называется функцией двух переменных величин x и y, если каждой паре допустимых значений x и y соответствует единственное значение z.
Функция двух переменных обозначается символом:
z = f (x, y) или z = z( x, y).
Систему значений x и y называют точкой М( x, y), а функцию двух переменных – функцией точки z = f (М).
Геометрическим изображением функции двух переменных является некоторая поверхность в пространстве.
Значение функции z = f (x, y) при x = a, y = b обозначается через f ( a, b).
Определение. Совокупностью всех точек, в которых определена функция двух переменных, называется областью существования или областью определения функции и является некоторая часть координатной плоскости, ограниченная одной или несколькими линиями ( или вся плоскость).
9.2. Предел и непрерывность функции двух переменных
Определение.
Число
называется пределом функции
при
и
(или в точке
),
если для любой последовательности точек
из области определения функции, отличных
от точки
и сходящихся к этой точке, соответствующая
последовательность значений функции
сходится к числу
,
и обозначается следующим образом
.
Пример.
Вычислить
.
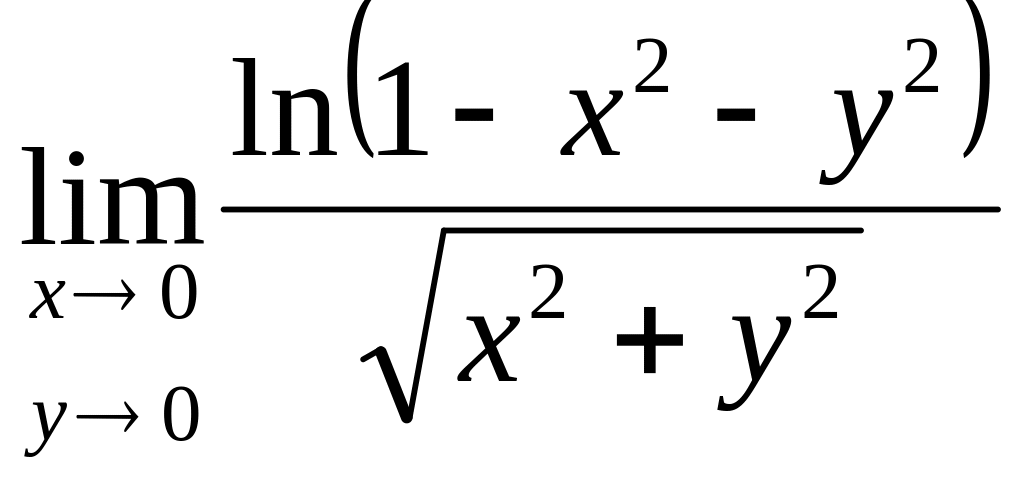Решение:
Обозначим
.
Условие
,
равносильно тому, что
.
Запишем предел в виде
.
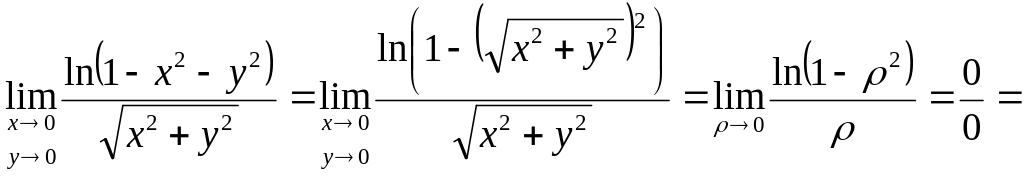
Определение. Функция называется непрерывной в точке , если она удовлетворяет трем условиям:
1. Определена в точке , то есть существует значение функции в этой точке;
2. Имеет конечный предел при и ;
3.
Предел функции в точке
равен значению функции в этой точке, то
есть
.
9.3. Частные производные и полный дифференциал функции двух переменных
Пусть есть функция от двух переменных х и у.
Дадим
переменной х
приращение
,
оставляя переменную у
неизменной.
Найдем новое значение функции
.
Определение.
Частным
приращением функции
по переменной
называется
разность между новым значением функции
и старым значением
и обозначается следующим образом:
.
Аналогично определяется и частное приращение функции z по аргументу y:
.
Дадим
приращение и переменной
и
переменной
.
Найдем новое значение функции
.
Определение. Полным приращением функции называется разность между новым значением функции и старым значением и обозначается следующим образом
.
Замечание. Полное приращение функции не равно сумме частных приращений, то есть
.
Определение. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю.
Для функции z =f(x,y) по определению имеем:
=
(x
,y)=
(частная производная по x),
(частная
производная по y).
При нахождении частной производной пользуются правилами дифференцирования функции одной переменной, считая другой аргумент постоянным.
Полный дифференциал функции z = f (x, y) вычисляется по формуле
dz
=
.
Функция, имеющая полный дифференциал, называется дифференцируемой.
Пример. Найти частные производные функций:
а).
;
б).
а). Считая y=const, имеем:
.
При
вычислении
нужно
считать x=const,
поэтому
.
б). Если y=const, то функция z является степенной функцией аргумента x, поэтому:
.
При x=const функция z – показательная функция аргумента y, поэтому:
.