3. Геометрические коэффициенты систем электродов
Очевидно, что мощность, развиваемая проходящим между электродами током, прямо пропорциональна квадрату приложенного к электродам напряжения, высоте электродов Н и удельной проводимости нагреваемой жидкости
,
(2)
где
- коэффициент пропорциональности,
численно равный, как следует из выражения,
мощности, развиваемой в межэлектродном
пространстве при напряжении на электродах,
высоте электродов и удельной проводимости
жидкости, находящейся между ними, равными
соответственно 1 В, 1 м и 1 См/м,
.
(3)
С учётом того, что
,
,
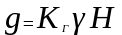(4)
откуда следует, что коэффициент численно равен также и проводимости жидкости, находящейся между электродами, при высоте электродов, равной 1м, и удельной проводимости жидкости (молока, воды и пр.), равной 1 См/м
.
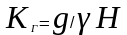(5)
Поскольку электроды расположены вертикально и параллельно друг другу, система электродов вполне однозначно может быть охарактеризована формой и размерами её поперечного сечения. Соотношение размеров этого сечения, как будет показано ниже, целиком определяется величину .
Для плоской однофазной системы электродов (рис.2а) мощность, развиваемая в межэлектродном пространстве
,
(6)
где
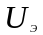- напряжение между противолежащими
электродами,
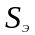- активная площадь электрода.
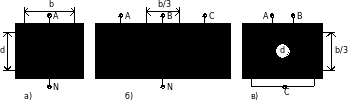
Рис.2. Поперечные сечения систем электродов с плоскими электродами.
Тогда
геометрический коэффициент этой системы
электродов, численно равный мощности
при напряжении между электродами, высоте
электродов и удельной проводимости
жидкости, находящейся между ними, равными
соответствующим единицам их измерения,
может быть найден делением мощности на
величину
.
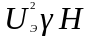В результате получим
.
(7)
Для трёхфазных, плоских систем электродов, изображённых на рисунке 2б и 2в
.
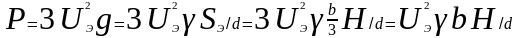(8)
Таким
образом, и для трёхфазных систем
электродов формула для нахождения
геометрического коэффициента аналогична
формуле, полученной для однофазной
системы электродов, но в качестве
величины
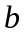в
формулу необходимо подставлять общую
ширину всех трёх электродов.
Для нахождения геометрического коэффициента концентрических систем электродов, изображённых на рисунке 3, воспользуемся обобщённой схемой концентрической системы электродов, приведённой на рисунке 3а.
Рис.3. Поперечные сечения систем электродов с концентрическими электродами.
Мощность, развиваемая проходящим между электродами током в элементарном слое dx
.
(9)
Поскольку
,
где Р – суммарная мощность межэлектродного пространства,
элементарная мощность в слое
.
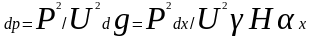(10)
Тогда мощность межэлектродного пространства может быть найдена путём решения полученного дифференциального уравнения интегрированием правой и левой её частей
.
(11)
Раскрыв предел, получим
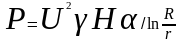(12)
или после замены радиусов на диаметры –
.
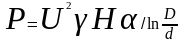(13)
Геометрический коэффициент системы электродов тогда будет равен
(14)
Полученное общее выражение геометрического коэффициента концентрической системы электродов пригодно для всех систем электродов, изображённых на рисунке 3. Необходимо только брать суммарный угол для всех электродов системы. Так для систем электродов, изображённых на рисунках 3в и 3г он будет равен 2 и 6 соответственно.
Анализируя выражения геометрического коэффициента, не трудно заметить, что его величина для любых систем электродов зависит от формы и соотношения размеров, характеризующих поперечное сечение системы электродов, и не зависят от самих размеров. Из этого следует, что все системы электродов, имеющие подобные сечения, имеют и равную величину геометрического коэффициента.
Учёт фазности систем электродов при определении геометрического коэффициента позволяет для любой системы электродов независимо от её конфигурации находить мощность в слое межэлектродного пространства по обобщённой формуле
,
(15)
или с учётом зависимости удельной проводимости от температуры
,
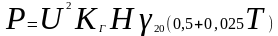(16)
где Н – высота слоя;
Т – температура жидкости в слое.
Эта же формула может использоваться и для трёхфазных систем электродов, изображённых на рисунке 4. В связи с тем, что некоторая часть объёма жидкости, находящейся в межэлектродном пространстве соединена в звезду, а другая часть соединена треугольником, аналитическое выражение геометрического коэффициента или отсутствует, или неудобно для практического использования из-за его сложности. Поэтому в таких случаях коэффициент может быть найден опытным путём. С этой целью для системы электродов определённой конфигурации и определённого соотношения размеров при известных напряжении, высоте электродов и удельной проводимости воды с помощью ваттметра или по показаниям амперметра и вольтметра определяется мощность. Далее по вышеприведённой формуле определяется геометрический коэффициент.
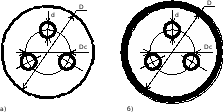
Рис.4. Трёхфазные системы электродов с общим: а) проводящим и б) изолированным баками.