§3 Встроенные функции системы имитак

Расширение аппарата системной динамики связано с тем, что ни все элементы имитационных моделей могут быть представлены линейными выражениями. При построении сложных моделей для адекватного отражения реальных процессов с помощью имитационных моделей недостаточно в правой части операторов модели- программы использовать только арифметические действия над эндогенными и экзогенными переменными. Такие действия как условные переходы, работы с массивами, имитации систем массового обслуживания требуют специальных выражений. Поэтому в системе ИМИТАК (как и в аналогичных программных продуктах, в основу которых положена методика системной динамики) введен ряд встроенных функций. Встроенные функции, не нарушая концепции системной динамики, дают возможность введения специальных функциональных преобразований.

Их немного, и они имеют определенную структуру. Так что понять и запомнить их нетрудно. В дальнейшем будут даны варианты реализаций различных функций, снабженных практическими примерами.

Любая встроенная функция имеет вид:

Ф. н = [имя встроенной функции]([АРГ1],[АРГ2]…)

Имя встроенной функции пишется латинскими буквами.

Аргументы же могут быть представлены:

1. В виде эндогенных переменных (Например, Ф. н =COS(А . н))

2. В виде экзогенных переменных (Например, Ф. н =SIN(КОНСТ))

3. В виде литералов (под литералами понимаются конкретные числа) (Например, Ф. н =CLIP(1,0,А.н, КОН1))

4. В виде других встроенных функций(Например, Ф. н =WHOLE(RAND(1,0),0))

Предлагается следующая классификация встроенных функций системы ИМИТАК:

1. Элементарные функции

2. Переключательные функции

3. Стохастические функции

4. Функции работы с числовыми массивами

5. Временные функции

6. Функции имитации систем массового обслуживания

7. Графические функции

§3.1. Элементарные функции

В этот класс собраны разнородные, логически несвязанные встроенные функции

Ф. н =SIN(А. н)- Синус

Ф. н = СОS(А. н)- Косинус

Ф. н =LOG(А. н)- Логарифм натуральный

Ф. н =EXP(А. н)- Экспонента

Ф. н =SIGN(А. н)- Анализ знака аргумента

Ф. н =RANGE(А. н, В. н)-Возведение в степень

Ф. н = MAX(А1. н,А2.н…)-Максимальное значение

Ф. н = MIN(А1. н,А2.н…)-Минимальное значение

Ф .н = WHOLE(А.н,К)-Округление

Рассмотрение работы отдельных функций мы будем вести на базе простейшей модели склада. При этом используем методику, которую определим как иерархия построения моделей. Иерархия построения моделей – это последовательное усложнение модели на основе ранее разработанных, более простых фрагментов этой модели. В качестве базового фрагмента мы будем использовать следующую модель склада.

Пример 2. На складе (С) первоначально имеется определенный запас продукта (товара; в нашем случае 1000 единиц). Каждый шаг моделирования на него поступает (ПОС) определенная партия товара (П) (в нашем случае 200 ед.) и со склада выбирается (ВЫБ) партия товара (В) (в нашем случае 300 ед.).Построить имитационную модель склада, работающего 20 шагов моделирования.

Начинаем строить имитационную модель, как показано в §2 Главы 1, с диаграммы потоков (Рис. 22):

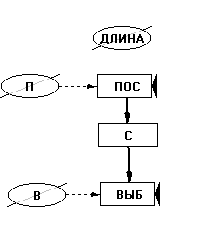
ис. 22. Диаграмма потоков модели склада

По данной диаграмме потоков нетрудно создать модель-программу и , если пропустить модель на компьютере, снабженном транслятором с системой VisualImitak, то мы получим следующие цифровые результаты для трех шагов моделирования:

Таблица 4. Модель-программа склада и результаты первых трех шагов моделирования.

МОДЕЛЬ-ПРОГРАММА	ВРЕМЯ=1	ВРЕМЯ=2	ВРЕМЯ=3
; Склад
У С.Н=С.П+ПОС.ПН-ВЫБ.ПН	С.1=1000	С.2=900	С.3=800
; Поступление
Т ПОС.НБ=П	ПОС.12=200	ПОС.23=200	ПОС.34=200
; Выборка
Т ВЫБ.НБ=В	ВЫБ.12=300	ВЫБ.23=300	ВЫБ.34=300
НАЧАЛЬНОЕ ЗНАЧЕНИЕ УРОВНЯ
И С=1000
; Поставка
К П=200
; Выдача
К В=300

По умолчанию числовые значения цикла рассчитываются при условии:

И ВРЕМЯ=0 (начальное значение цикла)

И DT=1 (шаг изменения времени внутри цикла)

И ДЛИНА=20 (продолжительность цикла).

Выше мы рассматривали цифровые результаты только для трех шагов, а теперь графические результаты будем анализировать для 20 шагов, как это было объявлено в условии задачи:

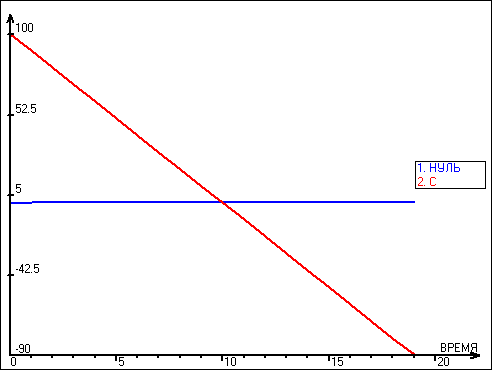
Рис. 23. Графический результат моделирования склада

На одиннадцатом шаге моделирования запасы на складе становятся отрицательными, что говорит о том, что в таком виде модель не может быть практически использована.

Это подтверждают и числовые результаты моделирования тех же переменных: приведенные в таблице 5.

Таблица 5. Числовые результаты моделирования склада

ВЫБ	ПОС	С
300	200	1000
300	200	900
300	200	800
300	200	700
300	200	600
300	200	500
300	200	400
300	200	300
300	200	200
300	200	100
300	200	0
300	200	-100
300	200	-200
300	200	-300
300	200	-400
300	200	-500

Разбор элементарных встроенных функций начнем с простейшей адаптации модели склада встроенными функциями синуса и косинуса. Многие из элементарных встроенных функций будем рассматривать попарно. Это не несет никакой смысловой нагрузки, а связано с двумя вспомогательными особенностями:

-они по жизни часто рассматриваются парами (например, SIN и COS, MIN и MAX)

-функции удобно рассматривать при построении модели склада, у которой есть входной темп – поступление и выходной – выборка. Это позволяет рассматривать, если это возможно сразу две функции.

Встроенная функция SIN

Встроенная функция COS

Для данных функций рассмотрим единый пример.

Пример 3. Первой адаптацией модели склада рассмотрим вариант, когда поставка (ПОС) будет функция синус, выборка (ВЫБ) – функция косинус Аргументами для обеих функций будет переменная ВРЕМЯ. Начальное значение склада (С) равным двум.

Диаграмма потоков представлена на Рис. 24.

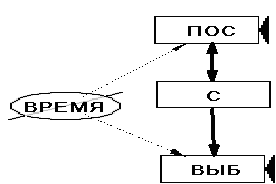
Рис. 24. Диаграмма потоков имитационной модели склада адаптированной тригонометрическими функциями

Программная реализация указанной модели-программы приведена в VisualImitak.

Таблица 6. Модель-программа склада с тригонометрическими функциями

	ВРЕМЯ=1	ВРЕМЯ=2	ВРЕМЯ =3
; Склад
У С.Н=С.П+ПОС.ПН-ВЫБ.ПН	С.1=2	С.2=1.698	С.3=0.373
; Поступление
Т ПОС.НБ=COS(ВРЕМЯ)	ПОС.12=0.54	ПОС.23=-0.41	ПОС.34=-0.989
; Выборка
Т ВЫБ.НБ=SIN(ВРЕМЯ)	ВЫБ.12=0.84	ВЫБ.23=0.909	ВЫБ.12=0.141
Е
; НАЧАЛЬНОЕ ЗНАЧЕНИЕ УРОВНЯ
И С=2

После пропуска имитационной модели на компьютере мы имеем график изменения переменных С, ПОС и ВЫБ на Рис. 25 . Результаты моделирования представленные в числовой форме заданы в Таблице 7

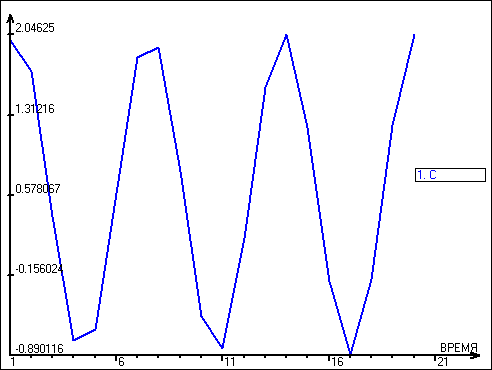
Рис. 25. Графики имитациионой модели склада адаптированного тригонометрическими функциями

Таблица 7. Результаты моделирования склада адаптированного тригонометрическими функциями

ВЫБ	ПОС	С
0.841471	0.540302	2
0.909297	-0.416147	1.69883
0.14112	-0.989992	0.373387
-0.756802	-0.653644	-0.757725
-0.958924	0.283662	-0.654567
-0.279415	0.96017	0.58802
0.656987	0.753902	1.82761

Анализ графических результатов показывает, что если аргументы тригонометрических функций задавать не непрерывно, а в радианах, то мы получим кусочно-линейные аппроксимации функций SIN и COS.

Рассмотрим так же спарено функции MIN и MAX,

Функция минимума (MIN)

Данная функция позволяет в каждый момент времени моделирования выбирать минимальное значение аргументов.

Общий вид функции: MIN (A1,A2,...)

Функция определена при любых значениях аргументов. Максимальное количество аргументов 15.

Функция максимума (MAX)

Данная функция позволяет в каждый момент времени моделирования выбирать максимальное из значений аргументов.

Общий вид функции: MAX (A1,A2,...)

Если для функций максимума и минимума количество аргументов больше 15, то можно использовать вложенность аргументов. Например, имеется следующий оператор:

Ф. н = MAX( А1.н, А2.н,…А15.н, А16.н).

где надо максимум выбрать из 17 аргументов

В этом случае задача решается следующим образом:

А17.н =MAX(А15.н,А16.н)

Ф. н = MAX(А1.н, А2.н,….А14.н, А17.н)

Кроме прямого назначения приведенных выше встроенных функций, они могут быть использованы для имитации некоторых логических ограничений в процессе реализации практических процессов.

Пример 4. Экономически не может быть оправдано наличие на складе отрицательных величин запасов. Для того, чтобы выдача со склада не переводила запасы в отрицательную величину, выходной темп ВЫБ должен быть представлен функцией MIN из текущих запасов на складе С и величины выдачи В. Однако отрицательное значение уровня может быть получено, если входной темп будет равен отрицательной величине. Защита от этого может быть достигнута если входной темп будет определен функцией MAX из поставки П и нуля , т.е. вместо отрицательного значения всегда будет входной темп ПОС будет равняться нулю. С учетом этого Пример 3 будет трансформирован в модель программу, приведенную в Таблице 8.

Таблица 8. Модель-программа склада для исправления семантических ошибок

МОДЕЛЬ-ПРОГРАММА	ВРЕМЯ=1	ВРЕМЯ=2	ВРЕМЯ=3	ВРЕМЯ=4
; Склад
У С.Н=С.П+ПОС.ПН-ВЫБ.ПН	С.1=1000	С.2=700	С.3=400	С.4=100
; Поступление
Т ПОС.НБ=MAX((П-С.Н),0)	ПОС.12=0	ПОС.23=0	ПОС.34=0	ПОС.45=100
; Выборка
Т ВЫБ.НБ=MIN(В,С.Н)	ВЫБ.12=300	ВЫБ.23=300	ВЫБ.34=300	ВЫБ.45=100
; НАЧАЛЬНОЕ ЗНАЧЕНИЕ УРОВНЯ
И С=1000
; Поставка
К П=200
; Выдача
К В=300

Приведенная выше таблица показывает, что уровень С уменьшается каждый шаг моделирования на 300 единиц. При этом переменная поступление (ПОС) до четвертого шага моделирования за счет отрицательной разности скобки (П-С.Н) будет равняться нулю. И только на четвертом шаге П-С.Н=200-100=100 , почему ПОС будет равняться 100. На том же четвертом шаге С.н=100 будет меньше чем В=300 и поэтому ВЫБ=100.

Функция экспоненты (EXP)

Экспоненциальная встроенная функция позволяет получать экспоненциальную зависимость от аргумента, который сам изменяется во времени. Общая форма представления этой функции:

Ф.Н= EXP(А.Н)

Механизм работы этой функции математически может быть выражен как

Ф(t)=е^А(t)

где е – основание натурального логарифма. При использовании функции возможно прерывание процесса при больших значениях А(t).

Функция возведение в степень (RANGE)

Функция возведения в степень осуществляет возведение некоторой переменной, являющейся функцией от времени, в степень задаваемой переменной, которая также зависит от времени. Общая форма записи функции:

Ф.Н=RANGE(А.Н,В.Н)

Механизм работы этой функции можно представить в следующем виде:

Ф(t)=А(t)^В(t)

При отрицательных значениях аргумента А(t) выходом функции будет иррациональное число, что не имеет смысла при моделировании реальных процессов, т. е. если А(t) меньше нуля при любом В(t) , то происходит программное прерывание. Прерывание, кроме того , происходит при достаточно больших А(t) и В(t) при переполнении разрядной сетки и если одновременно А(t)=0 и В(t)=0.

Чтобы проиллюстрировать использование этих функций рассмотрим пример имитации склада (Пример2), даже не прибегая к методике иерархии построения модели, а просто заменив в диаграмме потоков (Рис. 22) программное наполнение. В результате мы будем иметь следующую модель-программу, представленную в Таблице 9:

Таблица 9. Модель-программа склада с экспонентой и степенью

	ВРЕМЯ=1	ВРЕМЯ=2	ВРЕМЯ=3
; Склад
У С.Н=С.П+ПОС.ПН-ВЫБ.ПН	С.1=100	С.2=153.598	С.3=270.011
; Поставка
Т ПОС.НБ=EXP(ВРЕМЯ+3)	ПОС.12=54.5981	ПОС.23=148.413	ПОС.34=403.429
; Выборка
Т ВЫБ.НБ=RANGE(ВРЕМЯ,5)	ВЫБ.12=1	ВЫБ. 23=32	ВЫБ.34=243
Е
И С=100

Функция логарифма (LOG)

Функция позволяет получать логарифм от аргумента, изменяющегося во времени. Общий вид этой функции:

Ф.Н=LOG(А.Н)

Функция математически не определена в произвольном диапазоне изменения аргумента, и поэтому введено ограничение на аргумент. Так, если аргумент становится отрицательным или равным нулю, то машинный счет прерывается. Такое же прерывание может быть и при положительном аргументе, но близком к нулю. В этом случае прерывание происходит потому, что логарифм достигает значения, которое не помещается в разрядную сетку машины.

Функция знака (SIGN)

Результат данной функции зависит от знака аргумента: +1, если аргумент положителен, или -1, если аргумент отрицателен. Общая форма записи функции:

Ф.Н=SIGN (А.Н)

Математически действие, выполняемое данной функцией, можно выразить следующим образом:

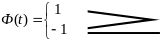
Эта функция условно отнесена к классу элементарных функций, хотя, по сути, она является прообразом переключательных функций. С помощью этой функции можно реализовать условные переходы. Чтобы проиллюстрировать использование этих функций рассмотрим пример имитации склада (Пример 3) заменив в диаграмме потоков (Рис. 22) программное наполнение. В результате мы будем иметь следующую модель-программу в таблице 10:

Таблица 10. Модель-программа склада с логарифмом и знаком

	ВРЕМЯ=1	ВРЕМЯ=2	ВРЕМЯ=3	ВРЕМЯ=4
; Склад
У С.Н=С.П+ПОС.ПН-ВЫБ.ПН	С.1=100	С.2 =50	С.3=0.6931	С.4=-48.2
; Поступление
Т ПОС.НБ=LOG(ВРЕМЯ)	ПОС.12=0	ПОС.23=0.69	ПОС.34=1.09	ПОС.45=1.38
; Выборка
Т ВЫБ.НБ=SIGN(С.Н)*50	ВЫБ.12=50	ВЫБ.23=50	ВЫБ.34=50	ВЫБ.45=-50
Е
; НАЧАЛЬНОЕ ЗНАЧЕНИЕ
И С=100

Функция округления (WHOLE )

Значение первого аргумента округляется до целого числа в зависимости от значения второго аргумента. Общий вид функции:

Ф. Н = WHOLE (A,K)

где А - округляемая величина;

К - константа, задающая режим округления.

Если К=1, то значение А округляется до ближайшего целого числа; если К<1, то округление происходит в меньшую сторону отбрасыванием дробной части; если К > 1, то выполняется округление до большего целого.

Пример 5. В некоторых случаях фрагмент имитационной модели может быть связан со следующей задачей: имеется объем товара, который должен быть расфасован на фиксированные группы (заказы) с определенным числом единиц товара в каждой группе. ( В качестве практического примера можно взять распределение конфет в новогодние подарки).Для решения этой задачи необходимо сначала определить, на какое максимально возможное число групп может быть разбит данный объем. Потом целое (максимальное) количество полученных групп передается из данного фрагмента в другие части имитационной модели. (Как вариант такая задача может состояться и при определении максимальной поставки товара в качестве заказов, т.е. максимально возможное число заказов. После определения максимального числа групп в текущем объеме нам может быть известен остаток товара, который меньше чем количество товара в одной группе). Если рассматривать это на примере производства, то это можно интерпретировать как количество готовой продукции – это целое число групп полученных при разбиении объема товара, а остаток - незавершенное производство. Рассмотрим это на простом примере. Пусто объем товара равняется 100 единицам, а число единиц в одной группе – 30 штук. Тогда число групп будет 100/30=3.В результате объем товара уменьшается на 3*30=90, при этом в остатке будем иметь 100-90=10.

Рассмотрим еще пример, но уже с выходом на модель-программу. Предположим, что мы имеем склад, с которого товара поступает на рынок только в виде массива сгруппированного товара. В результате в каждом шаге изымается максимальное число групп, а на складе остается только то, что мы имеем после изымания. Диаграмма потоков такой модели будет выглядеть как на Рис. 25.

Модель-программа, соответствующая данной диаграмме потоков

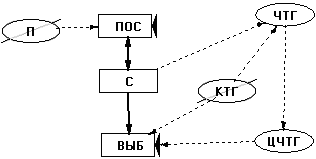
Рис. 25. Диаграмма потоков модели склада с группированием товара

Будет выглядеть следующим образом

Таблица 11. Модель-программа группирования заказов

	ВРЕМЯ=1	ВРЕМЯ=2	ВРЕМЯ=3
; Склад
У С.Н=С.П+ПОС.ПН-ВЫБ.ПН	С.1=400	С.2=309	С.3=303
; Число товарных групп
Д ЧТГ.Н=С.Н/КТГ	ЧТГ.1=23.52	ЧТГ.2=18.17	ЧТГ.3=17.82
; Целое число товарных групп
Д ЦЧТГ.Н=WHOLE(ЧТГ.Н,0)	ЦЧТГ.1=23	ЦЧТГ.2=18	ЦЧТГ.3=17
; Поступление
Т ПОС.НБ=П	ПОС.12=300	ПОС.23=300	ПОС.34=300
; Выборка
Т ВЫБ.НБ=ЦЧТГ.Н*КТГ	ВЫБ.12=391	ВЫБ.23=306	ВЫБ.34=289
Е
; НАЧАЛЬНОЕ ЗНАЧЕНИЕ УРОВНЯ
И С=400
; Поставка
К П=300
; Количество товара в группе
К КТГ=17

Результат пропуска модели на компьютере приведен на Рис. 26. Полученное в результате пилообразное графическое изображение можно объяснить следующим образом: пополнение запасов переменной на каждом шаге компенсируется восстановлением числа групп и, соответствующим повышенной выборки со склада. Так как поступление постоянно, то указанный процесс повторяется периодически.

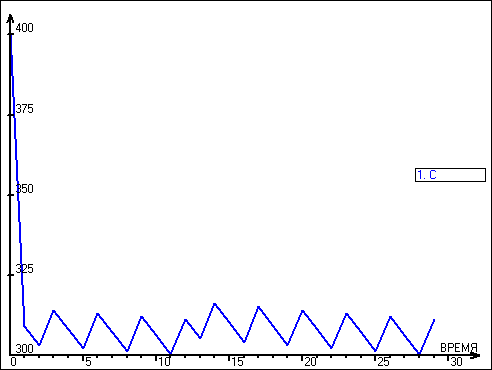
Рис. 26. Графические результаты модели с группировкой товара

Числовые результаты указанного моделирования приводятся в Таблице 12

Таблица 12. Числовые результаты модели с группировкой

ВЫБ	ПОС	С
391	300	400
306	300	309
289	300	303
306	300	314
306	300	308
289	300	302
306	300	313
306	300	307
289	300	301
306	300	312
306	300	306