
- •Учебно-методическое пособие по организации самостоятельной внеаудиторной работы студентов
- •«Математика»
- •Основного общего образования
- •Часть 1
- •Ярославль 2012 г.
- •Содержание
- •Пояснительная записка
- •Каждое задание включает в себя:
- •Как самостоятельно изучить теоретический материал
- •2. Как решать задачи (методика д. Пойа)
- •3. Как изготовить модель
- •Как пройти тестирование в программе MyTestStudent
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.1. Развитие понятия о числе Задание 1. Множества n, z, q. Действия с обыкновенными и десятичными дробями. – 2 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.1. Развитие понятия о числе Задание 2. Множества I, r, c. Действия над комплексными числами в алгебраической форме. – 2 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.1. Развитие понятия о числе Задание 3. Абсолютная и относительная погрешности – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 4. Преобразование рациональных выражений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 5. Решение линейных, квадратных, рациональных уравнений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 6. Корень п-й степени и его свойства. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 7. Решение иррациональных уравнений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 8. Степень с натуральным, целым, рациональным, действительным показателем. – 3 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 9. Решение показательных уравнений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 10. Логарифм числа. Применение свойств логарифма. – 4 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 11. Решение логарифмических уравнений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.2. Корни, степени и логарифмы Задание 12. Итоговое повторение по теме 1.2. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 13. Изготовление модели тригонометрического круга. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 14. Решение упражнений на вычисление значений тригонометрических выражений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 15. Решение задач на использование основных тригонометрических тождеств. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 16. Решение упражнений на вычисление значений тригонометрических выражений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 17. Решение задач на использование формул приведения. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 18. Решение задач на использование формул сложения. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 19. Решение задач на использование формул двойного угла. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 20. Решение задач на использование формул половинного угла. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 21. Решение задач на использование формул преобразования сумм тригонометрических функций в произведения и произведений в суммы. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 22. Решение задач на использование тангенса половинного аргумента. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 23. Преобразование тригонометрических выражений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 24. Решение простейших тригонометрических уравнений. – 2 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 25. Решение тригонометрических уравнений. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 26. Решение простейших тригонометрических неравенств. – 1 ч.
- •Раздел 1. Алгебра и начала анализа
- •Тема 1.3. Основы тригонометрии Задание 27. Итоговое повторение по теме 1.3. – 1 ч.
- •Критерии оценки выполнения самостоятельной внеаудиторной работы
- •Список рекомендуемой литературы
- •Логарифм и его свойства
- •Значения тригонометрических функций
- •Знаки тригонометрических функций
- •Основные тригонометрические формулы
- •I группа. Соотношения между тригонометрическими функциями одного аргумента:
- •IV группа. Формулы сложения:
- •VI группа. Формулы преобразования произведений тригонометрических функций в сумму и разность:
- •Решение простейших тригонометрических уравнений
Раздел 1. Алгебра и начала анализа
Тема 1.2. Корни, степени и логарифмы Задание 6. Корень п-й степени и его свойства. – 1 ч.
Цель: формирование умения применять определение и свойства арифметического корня n–й степени.
Задание для самостоятельной внеаудиторной работы:
6.1. Вспомните, что называют арифметическим корнем n–й степени из числа а. Перечислите свойства арифметического корня n–й степени.
Основные сведения из теории:
6.2. Закончите определение:
Корнем n–й степени
из числа а (![]() )
называют такое число, … степень
которого равна …
)
называют такое число, … степень
которого равна …
6.3. Продолжите важные свойства корня n–й степени:
 …
… …
… …
… …
… …
…
Примеры и упражнения:
6.4. Вычислите:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
6.5. Найдите значение выражения:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
6.6. Вынесите множители из-под знака корня:
а)
![]() ;
б)
;
б)
![]() .
.
6.7. Упростите выражение:
а)
![]() ;
б)
;
б)
![]() .
.
6.8. Вычислите:
а)
![]() ;
б*)
;
б*)![]() ;
в)
;
в)
![]() .
.
Указание: * - попробуйте выражение под квадратным корнем представить в виде
6.9. Пройдите тесты на умение преобразовывать выражения, содержащие корень п-й степени:
http://reshuege.ru/test?theme=56&ttest=true;
http://ipo.spb.ru/iumk2/MATH_XXI-10/Tests/Test_2.1.1/T_2.1.1.html.
Список литературы:
1. Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков. - М.: Изд. центр "Академия", 2010. - 304с. – Глава 1, стр. 10 – 13.
2. Гипермаркет знаний – понятие корня п-й степени из неотрицательного числа. http://school.xvatit.com/.
Раздел 1. Алгебра и начала анализа
Тема 1.2. Корни, степени и логарифмы Задание 7. Решение иррациональных уравнений. – 1 ч.
Цель: формирование умения решать иррациональные уравнения.
Задание для самостоятельной внеаудиторной работы:
7.1. Вспомните, какие уравнения называются иррациональными. Какова техника их решения?
Основные сведения из теории:
7.2. Закончите определение:
Уравнение, содержащее неизвестную переменную … называется иррациональным.
7.3. Продолжите высказывания:
метод решения иррациональных уравнений – возведение …
обязательными этапами решения являются запись … и выполнение …
Примеры и упражнения:
7.4. Решите иррациональные уравнения:
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() .
.
7.5. Решите иррациональные уравнения:
а![]() )
)
![]() б)
б)
7.6. Пройдите тест на решение иррациональных уравнений:
http://reshuege.ru/test?theme=10&ttest=true.
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 1, §11, п. 1, стр. 94 – 95.
Раздел 1. Алгебра и начала анализа
Тема 1.2. Корни, степени и логарифмы Задание 8. Степень с натуральным, целым, рациональным, действительным показателем. – 3 ч.
Цель: формирование умения выполнять преобразования алгебраических выражений, содержащих степени с действительным показателем.
Задание для самостоятельной внеаудиторной работы:
8.1. Дайте определение степени числа а с натуральным, целым, рациональным показателем. Перечислите свойства степени.
Основные сведения из теории:
8.2. Закончите определение:
 ,
где
;
,
где
;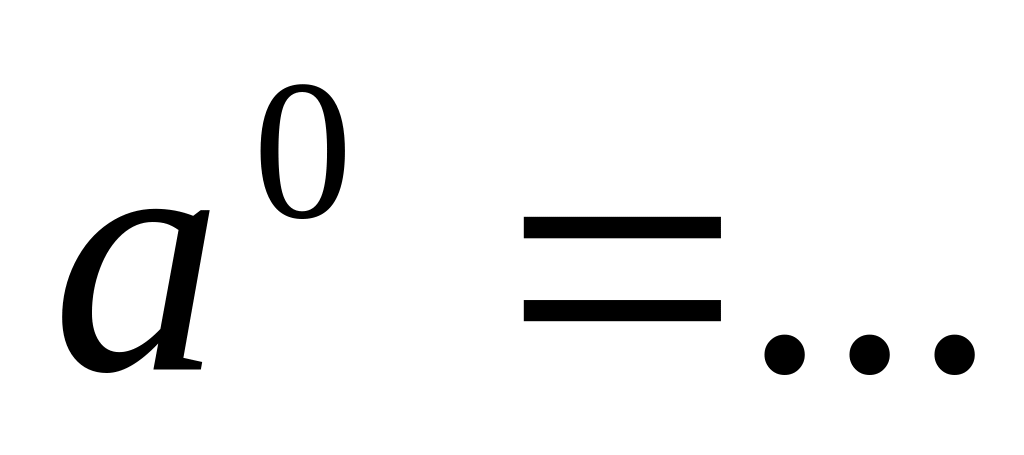 ;
;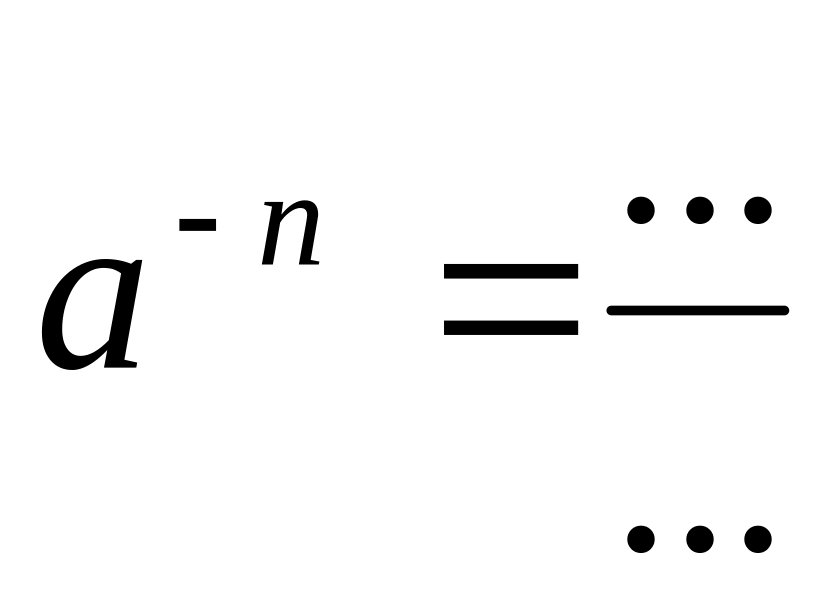 ,
где
;
,
где
; ,
где
,
где
 ,
.
,
.
8.3. Продолжите основные свойства степени:
 ;
; ;
; ;
; ;
;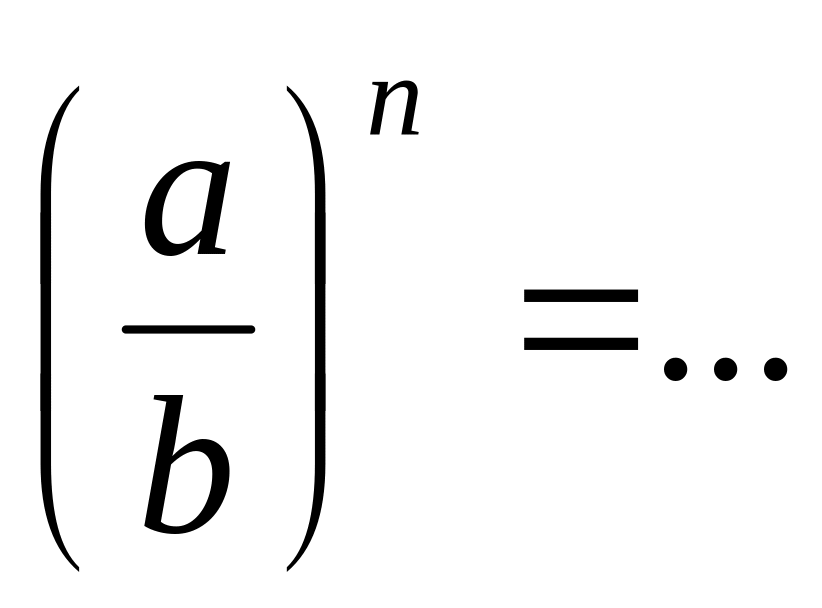 ;
;
Примеры и упражнения:
При выполнении заданий по теме «Степень с натуральным, целым, рациональным, действительным показателем», мы будем обращаться к одному из драгоценных камней, который по блеску, красоте превосходит все минералы. Познакомимся с понятиями, которые используются в его добыче, обработке, с историей некоторых камней.
8.4. Заполните таблицу:
Буква |
Пример |
Ответ |
Буква |
Пример |
Ответ |
Буква |
Пример |
Ответ |
Б |
|
|
Й |
|
|
З |
|
|
Ы |
|
|
С |
|
|
О |
|
|
Е |
|
|
Н |
|
|
А |
|
|
П |
|
|
Л |
|
|
М |
|
|
И |
|
|
Д |
|
|
|
|
|

 8.5.
Найдите значение выражений и заполните
таблицу:
8.5.
Найдите значение выражений и заполните
таблицу:
Номер |
Пример |
Ответ |
Буква |
Номер |
Пример |
Ответ |
Буква |
1 |
|
|
|
5 |
|
|
|
2 |
|
|
|
6 |
|
|
|
3 |
|
|
|
7 |
|
|
|
4 |
|
|
|
8 |
|
|
|

 8.6.
Заполните таблицу:
8.6.
Заполните таблицу:
Выражение |
Выражение в виде степени с рац. показателем |
Слова |
|
|
шатер |
|
|
павильон |
|
|
остриё |
|
|
коронка |
|
|
плато |
|
|
арена |
|
|
площадка |
|
|
крыша |


8.7. Найдите значение выражений и заполните таблицу.
Номер |
Пример |
Ответ |
Название |
Пример |
Ответ = Масса |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
Выполнив это задание, Вы узнаете о самых знаменитых алмазах мира, у которых есть своя судьба.
Карта ответов (название алмаза):
Екатерина |
Царь Пётр |
Меньшиков |
Орлов |
Кохинор |
Шах |
0 |
0,5 |
1 |
2 |
4 |
8 |
М асса
драгоценных камней измеряется каратами:
1 карат = 0,2 г. Алмазы, имеющие массу более
53 карат, получают собственные имена.
Наиболее крупные драгоценные камни
России хранятся в Алмазном фонде страны,
расположенном в Московском Кремле.
асса
драгоценных камней измеряется каратами:
1 карат = 0,2 г. Алмазы, имеющие массу более
53 карат, получают собственные имена.
Наиболее крупные драгоценные камни
России хранятся в Алмазном фонде страны,
расположенном в Московском Кремле.
1) Одним из самых знаменитых бриллиантов является алмаз №1. Он был найден в Индии, затем попал в у «Персию», а в 1829 году был привезен в Россию в качестве выкупа за смерть А.С. Грибоедова.
3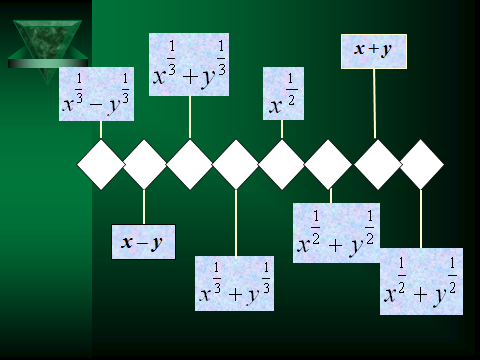 )
В алмазном фонде хранится еще один
знаменитый бриллиант - №3. Он также был
найден в Индии» в XVII веке и имел до
огранки массу около 400 карат. После
огранки бриллиант получил имя «Дерианур»
- «море света». Алмаз неоднократно
похищался, попадал в различные страны
и к разным правителям. В 1773 году его
приобрел фаворит Екатерины II Граф
Григорий Орлов в дар императрице. Имя
алмаза было изменено. Бриллиант был
вставлен в Российский державный скипетр.
)
В алмазном фонде хранится еще один
знаменитый бриллиант - №3. Он также был
найден в Индии» в XVII веке и имел до
огранки массу около 400 карат. После
огранки бриллиант получил имя «Дерианур»
- «море света». Алмаз неоднократно
похищался, попадал в различные страны
и к разным правителям. В 1773 году его
приобрел фаворит Екатерины II Граф
Григорий Орлов в дар императрице. Имя
алмаза было изменено. Бриллиант был
вставлен в Российский державный скипетр.
8.8. Упростите выражение:

Упростив выражение, заполните пропуски на рисунке. Вы получите название крупнейшего в мире алмаза.
Долгое время основным местом добычи алмазов была Индия, а в начале XX века были открыты месторождения в Южной Африке. Там в 1905 году на одном из приисков был найден крупнейший алмаз, масса которого составляла 3106 карат, что равно 621 грамму. Он был назван именем хозяина прииска.
При огранке этот алмаз был рассечен на 9 частей. Наибольшая часть, имеющая массу 530 карат, была названа «Звезда Африки». Этот бриллиант, имеющий 74 грани, стал украшать британский державный скипетр.
8.9. Пройдите тесты на умение выполнять действия со степенями:
http://le-savchen.ucoz.ru/publ/4 (корни и степени - 3 теста);
http://reshuege.ru/test?theme=61&ttest=true;
http://reshuege.ru/test?theme=57&ttest=true;
http://reshuege.ru/test?theme=62&ttest=true.
Список литературы:
1. Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков. - М.: Изд. центр "Академия", 2010. - 304с. – Глава 1, стр. 13 – 16.
2. http://mirurokov.ru/otkrytyi-urok/25-vozvedenie-v-stepen/99-stepen-s-racionalnym-pokazatelem.html.


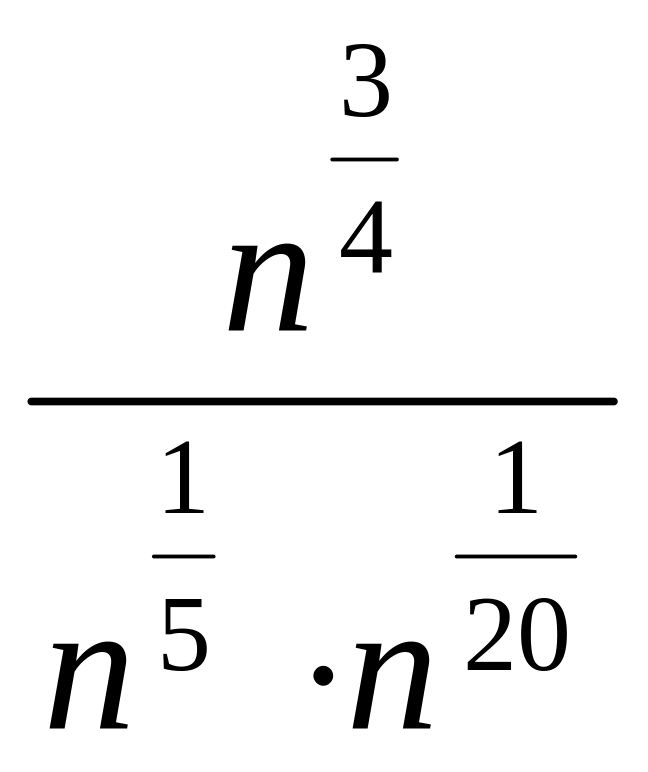 при n
= 81
при n
= 81