Раздел 1. Алгебра и начала анализа

Тема 1.3. Основы тригонометрии Задание 18. Решение задач на использование формул сложения. – 1 ч.

Цель: формирование умения использовать формулы сложения для преобразования и вычисления значений тригонометрических выражений.

Задание для самостоятельной внеаудиторной работы:

 18.1. Вспомните, какие формулы называют формулами сложения. Запишите эти формулы. Внимательно изучите по учебнику простейшие примеры применения формул сложения.

Основные сведения из теории:

18.2. Закончите определение:

Формулами сложения называются формулы, выражающие тригонометрические функции углов через …

18.3. Замените символ * так, чтобы выражение стало формулой сложения:

• ;

• ;

• .

Примеры и упражнения:

18.4. Упростите выражение:

а) ; б) ; в) ; г) .

18.5. Вычислите, применяя формулы сложения:

а) ; б) ; в) ;

г) ; д) ; е) ; ж) .

18.6. Вычислите, применяя формулы сложения:

а) ; б) ; в) ; г) ; д) ; е) .

18.7. Найдите значение выражения:

а) ; б) ; в) , если и .

Список литературы:

1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. - Глава 3, §31, стр. 157 – 160.

Раздел 1. Алгебра и начала анализа

Тема 1.3. Основы тригонометрии Задание 19. Решение задач на использование формул двойного угла. – 1 ч.

Цель: формирование умения использовать формулы двойного угла для преобразования и вычисления значений тригонометрических выражений.

Задание для самостоятельной внеаудиторной работы:

 19.1. Вспомните, какие формулы называют формулами двойного угла. Запишите эти формулы. Внимательно изучите по учебнику простейшие примеры применения формул двойного угла.

Основные сведения из теории:

19.2. Закончите определение:

Формулами двойного угла называются формулы, выражающие тригонометрические функции двойного угла через …

19.3. Замените символ * так, чтобы выражение стало формулой двойного угла:

• ;

• ;

• .

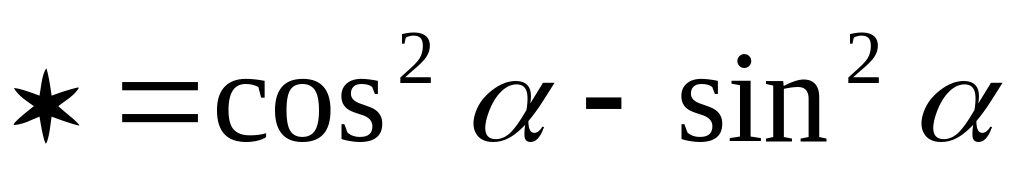19.4. Установите соответствие:

ВЫРАЖЕНИЕ	РЕЗУЛЬТАТ УПРОЩЕНИЯ ВЫРАЖЕНИЯ
1.	А.
2.	Б.
	В.
	Г.
	Д.
	Е.
	Ж.
	З.

Примеры и упражнения:

19.5. Вычислите, применяя формулы двойного угла:

а) ; б) ; в) ;

г) ; д) .

19.6. Упростите выражение:

а) ; б) ; в) ; г) ; д) ;

е) ; ж) ; з) ; и) .

19.7. Найдите значение выражения:

а) , если ; б) , если ; в) , если и .

19.8. Вычислите:

а) ; б) , если .

19.9. Пройдите тест на применение формул двойного угла. Электронная версия теста «Тест 19» находится на прилагаемом к пособию диске.

Список литературы:

1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. - Глава 3, §32, стр. 160 – 162.