Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гомельский Государственный Технический Университет им. П.О. Сухого

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Часть_5(№14-№17).doc

Скачиваний:

Добавлен:

17.11.2019

Размер:

2.98 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

4 Провести полное исследование и построить кривую, заданную параметрическими уравнениями :

№			№
1	2	3	4	5	6
4.1			4.11
4.2			4.12
4.3			4.13

1	2	3	4	5	6
4.4			4.14
4.5			4.15
4.6			4.16
4.7			4.17
4.8			4.18
4.9			4.19
4.10			4.20

Решение типовых примеров

1.20 Найти естественную область определения функции , её интервалы выпуклости и точки перегиба, если

Решение. . Имеем:

, .

Вторая производная не обращается в нуль ни при каких значениях и не существует в точке . В окрестности точки получим при , то и кривая выпукла вверх, при , то и кривая выпукла вниз. Следовательно, – точка перегиба, при этом 2.

2.20 Найти естественную область определения функции и асимптоты к её графику, если .

Решение.

1) функция определена на промежутках

Так как

, ,

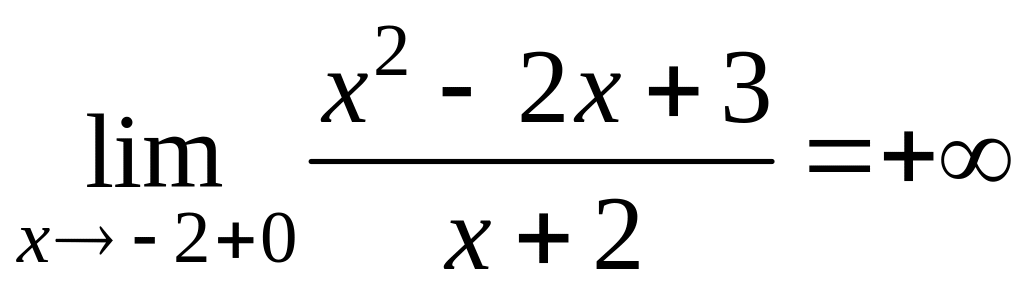то прямая является вертикальной асимптотой.

2) наклонные асимптоты:

Следовательно, наклонная асимптота при имеет вид

3) горизонтальных асимптот нет, так как

2.21 Найти естественную область определения функции и асимптоты к её графику, если .

Решение. Преобразуем функцию к виду

1) функция определена на промежутках

Так как

, а не существует,

то прямая является вертикальной асимптотой.

2) наклонные асимптоты:

Следовательно, наклонная асимптота при имеет вид

Аналогично,

Следовательно, наклонная асимптота при имеет вид

3) горизонтальных асимптот нет, так как

, .

3.20 Найти естественную область определения функции , провести полное исследование и построить её график, если

Решение. Для построения графика функции проведем ее исследование по приведенной схеме.

1) Находим , определяем точки разрыва, нули, точки пересечения графика функции с осью , периодичность, симметрию. Функция не определена в точках, где знаменатель обращается в нуль, т. е. при , . Следовательно, область определения есть

Исследуем поведение функции в окрестностях точек , :

, ,

, .

Следовательно, точки , являются точками разрыва второго рода. Поскольку и , то функция не ограничена при .

График функции пересекает координатные оси только в начале координат, так как .

Функция не является периодичной.

Функция нечетная, так как область определения симметрична и , т. е.

Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для .

2) Асимптоты графика функции. Поскольку односторонние пределы в точках , равны бесконечности, то прямые и являются вертикальными асимптотами графика функции.

Вычислим пределы:

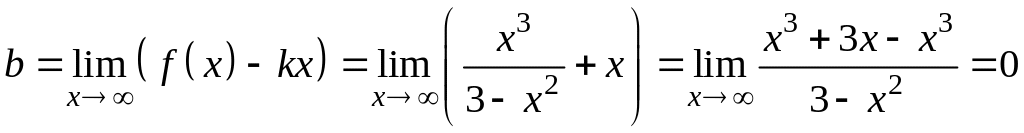Прямая является наклонной асимптотой к графику функции при .

3) Точки возможного экстремума и интервалы монотонности функции. Находим первую производную функции:

Функция определена на . В промежутке производная обращается в нуль в точках , .

Определяем интервалы монотонности из неравенств и для любого . Имеем:

, ,

т. е. функция возрастает на интервалах и .

Аналогично:

, ,

т. е. функция убывает на множестве .

4) Промежутки выпуклости, точки перегиба. Вычисляем вторую производную функции :

Функция определена на области определения .

Находим интервалы выпуклости графика функции из неравенств , для любого . Имеем:

т. е. кривая выпукла вниз на .

Аналогично:

т. е. кривая выпукла вверх на .

В точке имеем и в окрестности , а в окрестности . Значит, точка кривой с абсциссой отделяет интервал выпуклости вниз кривой от ее интервала выпуклости вверх. Поэтому является точкой перегиба кривой.

5) Локальные экстремумы. Определяем с помощью второй производной локальные экстремумы. Так как , точка с абсциссой является точкой локального максимума. В силу симметрии графика функции, точка с абсциссой является точкой локального минимума. Итак, , .

Результаты исследования функции заносим в таблицу 1.

Таблица 1 – Результаты исследования функции

0				3
0	+	Не сущ.	+	0	–
0	+	Не сущ.	–	–	–
0		Не сущ.		-4,5
(т.перег)

Исходя из результатов, содержащихся в таблице 1, строим график данной функции для . Используя нечетность функции, достраиваем ее график на всей области определения (рисунок 22).

Рисунок 22 – График функции

4.20 Провести полное исследование и построить кривую, заданную параметрическими уравнениями

, .

Решение. Решая уравнение относительно переменной , получим , при .

Рисунок 23 – График функции

I шаг. При имеем . Тогда, подставляя в параметрическое задание кривой для , получим

, при .

Проведем полное исследование функции

, при по схеме из задачи 3.20.

1) . Исследуем поведение функции при :

Находим точки пересечения с осью OX: 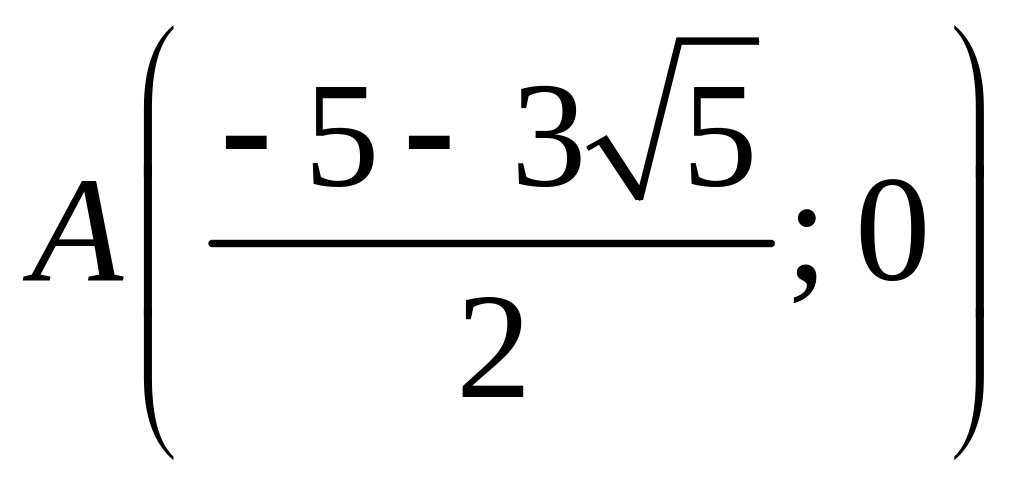, . График пересекает ось OY в точке . Функция не является периодической, общего вида.

2) Вычислим пределы:

, .

Следовательно, наклонных асимптот нет.

3) Находим первую производную функции :

Производная обращается в ноль в точке и не существует в точке . Определяем интервалы монотонности из неравенств и при . Функция возрастает на , убывает на . Таким образом, имеем локальный минимум в точке .