6 Найти для данной функции, заданной на естественной области определения.

№		№
1	2	3	4
6.1		6.11
6.2		6.12
1	2	3	4
6.3		6.13
6.4		6.14
6.5		6.15
6.6		6.16
6.7		6.17
6.8		6.18
6.9		6.19
6.10		6.20

7 Найти производную второго порядка от функции заданной парамет­рически.

№
1	2
7.1
7.2
7.3
7.4
7.5

1	2
7.6
7.7
7.8
7.9
7.10
7.11
7.12
7.13
7.14
7.15
7.16
7.17
7.18
7.19
7.20

8 Для функции , заданной неявно в окрестности точки и имею­щий в этой окрестности вторую производную, найти .

№		№
8.1		8.11
8.2		8.12
8.3		8.13
8.4		8.14
8.5		8.15
8.6		8.16
8.7		8.17
8.8		8.18
8.9		8.19
8.10		8.20

Решение типовых примеров

1.20 Для данной функции , заданной в естественной области определения, найти производную второго порядка. Записать .

Решение. Найдём сначала :

.

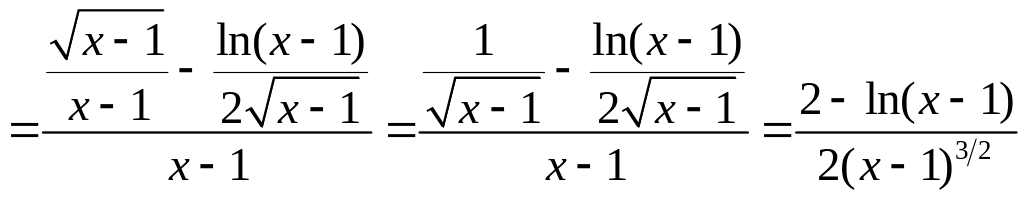Теперь

.

.

2.20 Проверить, удовлетворяет ли данная функция, заданная в естест­вен­ной области определения, данному уравнению:

, .

Решение. Найдём . Теперь

.

Подставим и в данное уравнение:

.

Получили верное равенство. Значит, данная функция удовлетворяет дан­ному уравнению.

3.20 Пусть – трижды дифференцируемая функция на всей число­вой прямой. Найти и для сложной функции , заданной на естественной области определения.

Решение. Если , f – дифференцируемая функция, то

.

Тогда ,

.

4.20 Найти производную n-го порядка для функции , заданной на естественной области определения.

Решение. Для найдём несколько производных:

, , , , …

Заметим, что

,

,

,

.

Теперь можно заметить, что (более строго это можно доказать, используя метод математической индукции).

5.20 Используя, формулу Лейбница найти производную указан­ного порядка k=24 функции , заданной на естественной об­ласти определения.

Решение Воспользуемся формулой Лейбница:

, где .

Пусть , . Тогда , . Для .

, , … , .

По формуле Лейбница

.

6.20 Найти для данной функции ,заданной на естественной области определения.

Решение. Преобразуем данную функцию:

Используя формулу , получим

.

7.20 Найти производную второго порядка от функции задан­ной параметрически:

.

Решение. Равенства задают параметрически функ­цию , так как при функция монотонно возрастает. Согласно теореме о производной функции, заданной параметрически, дифференцируема.

Найдём сначала , . Тогда .

Для нахождения найдём сначала

.

Теперь .

Замечание 1. Для нахождения можно было воспользоваться форму­лой:

.

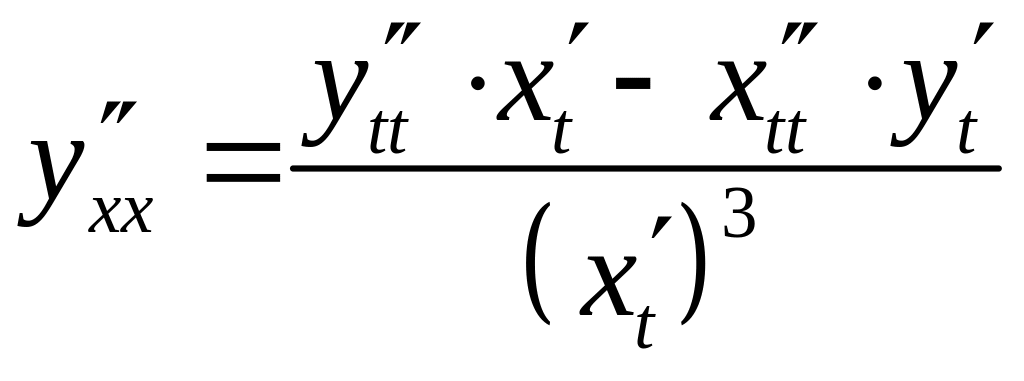Замечание 2. В данном случаем из равенства логично выразить явно , тогда , и производные можно вычислить непосредст­венно.

8.20 Для функции , заданной не­явно в окрестности точки и имеющей в этой окрестности вторую производную, найти .

Решение. Найдём сначала . Продифференцируем обе части данного равенства но x, учитывая, что y есть функция от x. Получим:

.

Отсюда , .

Подставив в данное в условии равенство , найдём .

Тогда .

Теперь .

Подставив сюда , , , получим .

Лабораторная работа № 15

Основные теоремы дифференциального исчисления: примеры применения теорем. Правило Лопиталя.

Необходимые понятия и теоремы: теорема Ролля, теорема Лагранжа, формула конечных приращений, правило Лопиталя раскрытия неопределенностей и , раскрытие неопределенностей вида , , , , .

Литература: [1] с. 254 – 263, [2] с. 164 – 172.