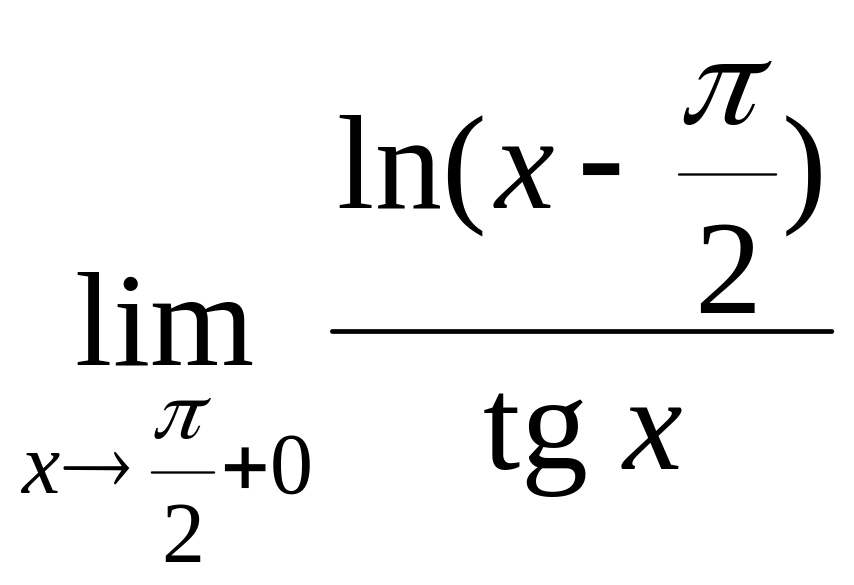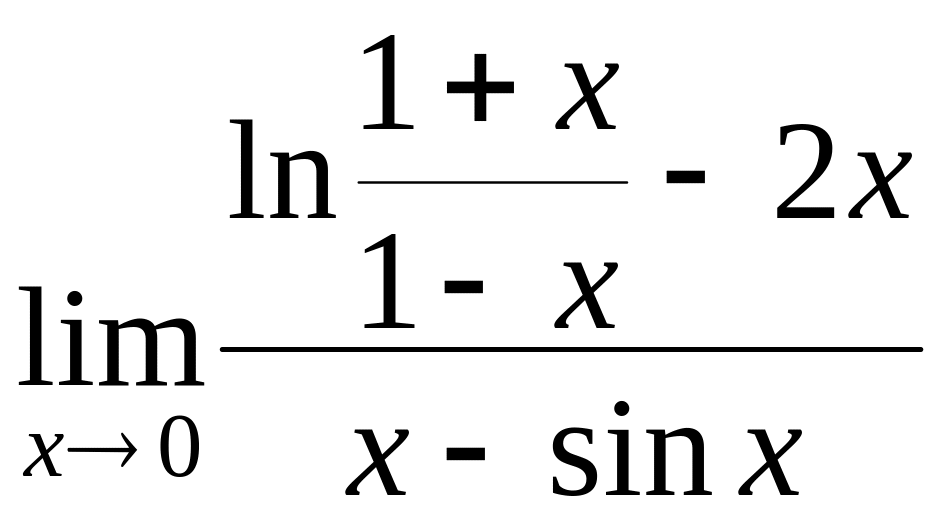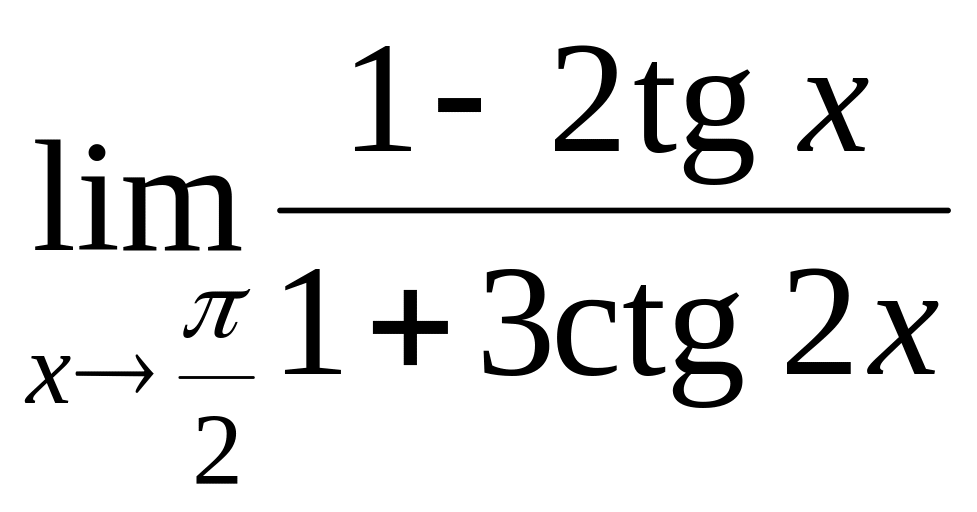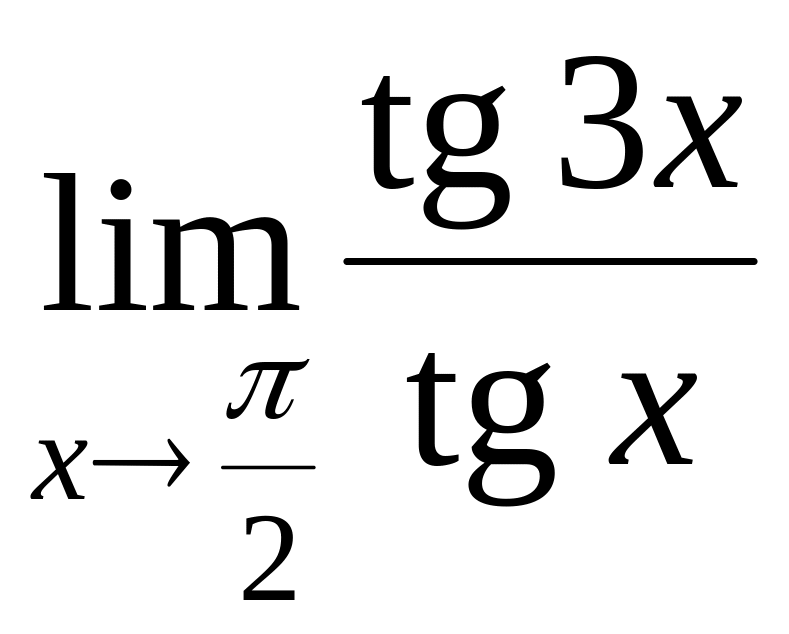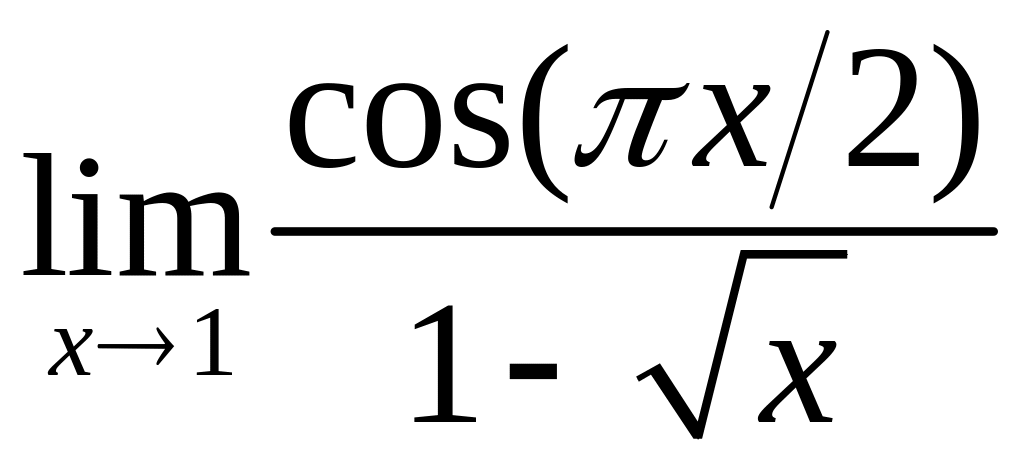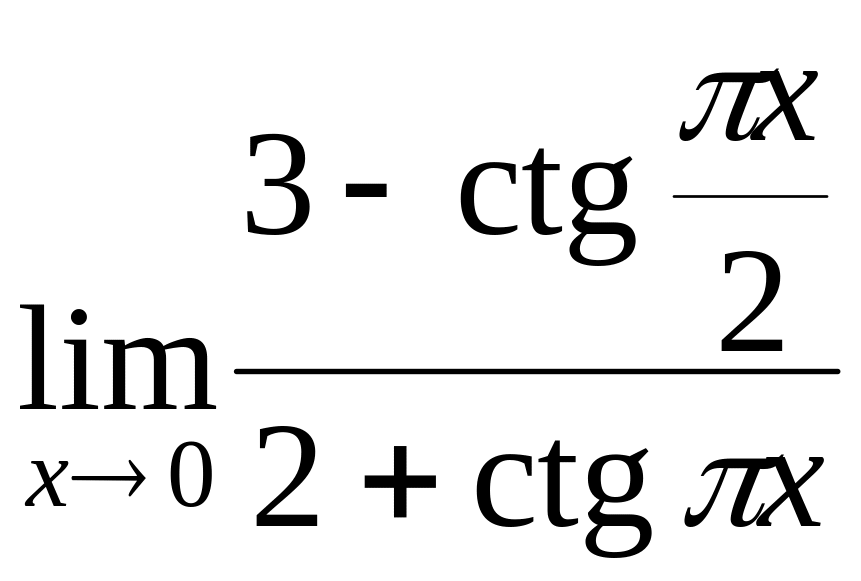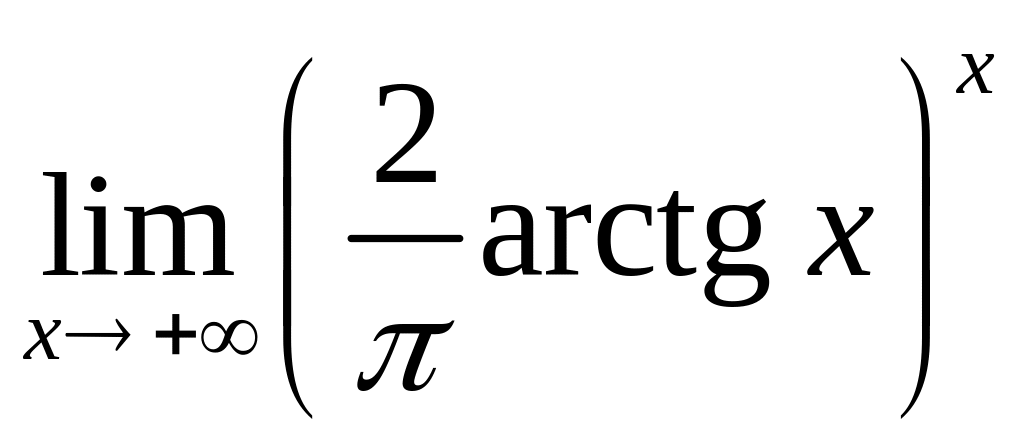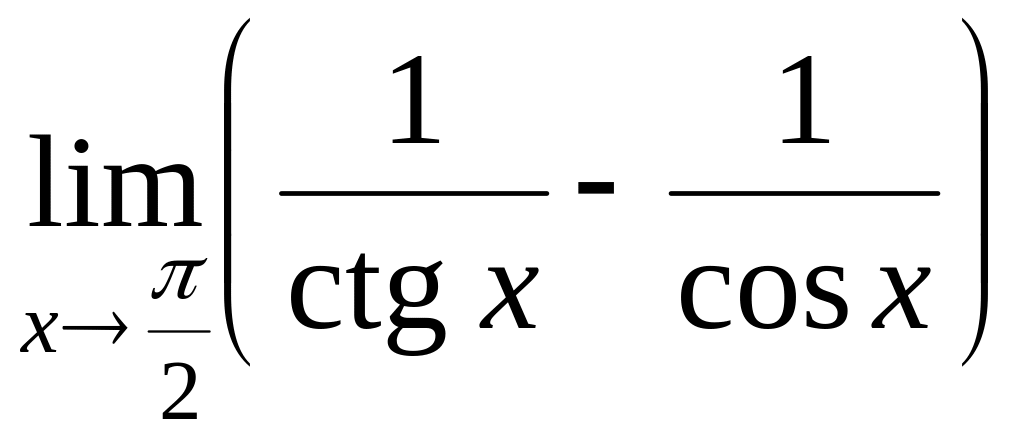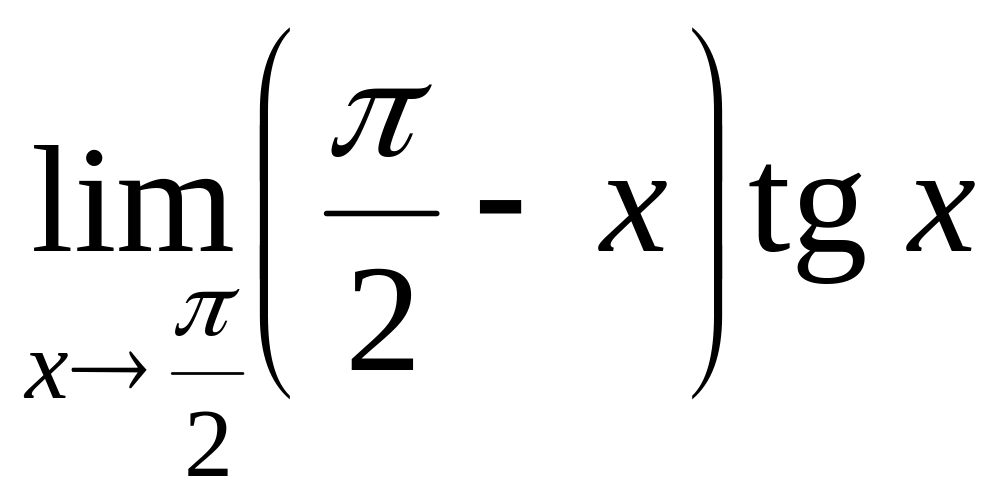- •1 Для данной функции , заданной в естественной области определения, найти производную второго порядка. Записать .
- •2 Проверить, удовлетворяет ли функция , заданная в естественной области определения, данному уравнению.
- •3 Пусть – трижды дифференцируемая функция на всей числовой прямой. Найти и для сложной функции , заданной на естественной области определения.
- •4 Найти производную n-го порядка для функции, заданной на естественной области определения.
- •5 Используя, формулу Лейбница найти производную указанного порядка k функции , заданной на естественной области определения.
- •6 Найти для данной функции, заданной на естественной области определения.
- •7 Найти производную второго порядка от функции заданной параметрически.
- •8 Для функции , заданной неявно в окрестности точки и имеющий в этой окрестности вторую производную, найти .
- •Решение типовых примеров
- •1 Проверить справедливость теоремы Ролля для данной функции на указанном отрезке :
- •2 Для данной функции и указанного отрезка найдите точку , такую, что (или покажите, что такая точка существует):
- •3 Используя теорему Лагранжа, докажите неравенство при указанных значениях переменных:
- •4 С помощью правила Лопиталя вычислить следующие пределы:
- •5 Установить вид неопределенности в данных пределах. Преобразовав имеющиеся неопределенности к виду или , вычислить предел с помощью правила Лопиталя.
- •Решение типовых примеров
- •1 Найти естественную область определения функции , ее интервалы монотонности и точки экстремума:
- •2 Найти глобальный экстремум функции , определенной на :
- •3 Найти глобальный экстремум функции , определенной на :
- •Решение типовых примеров
- •2.20 Найти глобальный экстремум функции , определенной на :
- •5.20 Решить физическую задачу:
- •1 Найти естественную область определения функции , интервалы, где выпукла, и точки перегиба:
- •2 Найти естественную область определения функции и асимптоты к её графику:
- •3 Найти естественную область определения функции , провести полное исследование и построить её график:
- •4 Провести полное исследование и построить кривую, заданную параметрическими уравнениями :
- •Решение типовых примеров
- •II шаг. При имеем . Тогда, подставляя в параметрическое задание кривой для , получим
4 С помощью правила Лопиталя вычислить следующие пределы:
№ |
а) |
б) |
1 |
2 |
3 |
4.1 |
|
|
4.2 |
|
|
4.3 |
|
|
4.4 |
|
|
4.5 |
|
|
4.6 |
|
|
4.7 |
|
|
4.8 |
|
|
4.9 |
|
|
4.10 |
|
|
1 |
2 |
3 |
4.11 |
|
|
4.12 |
|
|
4.13 |
|
|
4.14 |
|
|
4.15 |
|
|
4.16 |
|
|
4.17 |
|
|
4.18 |
|
|
4.19 |
|
|
4.20 |
|
|
5 Установить вид неопределенности в данных пределах. Преобразовав имеющиеся неопределенности к виду или , вычислить предел с помощью правила Лопиталя.
№ |
а) |
б) |
в) |
1 |
2 |
3 |
4 |
5.1 |
|
|
|
5.2 |
|
|
|
5.3 |
|
|
|
5.4 |
|
|
|
5.5 |
|
|
|
5.6 |
|
|
|
5.7 |
|
|
|
5.8 |
|
|
|
5.9 |
|
|
|
1 |
2 |
3 |
4 |
5.10 |
|
|
|
5.11 |
|
|
|
5.12 |
|
|
|
5.13 |
|
|
|
5.14 |
|
|
|
5.15 |
|
|
|
5.16 |
|
|
|
5.17 |
|
|
|
5.18 |
|
|
|
5.19 |
|
|
|
1 |
2 |
3 |
4 |
5.20 |
|
|
|
Решение типовых примеров
1.20 Проверить
справедливость теоремы Ролля для функции
![]() на отрезке
.
на отрезке
.
Решение.
Данная функция непрерывна на отрезке
,
дифференцируема на интервале
![]() .
Кроме того, выполняются условия:
.
Кроме того, выполняются условия:
![]() .
Значит, на интервале
существует такая точка
.
Значит, на интервале
существует такая точка
![]() ,
что
,
что
![]() ,
т. е. теорема Ролля для данной функции
справедлива.
,
т. е. теорема Ролля для данной функции
справедлива.
В данном примере
точку
можно найти.
Действительно, рассмотрим уравнение
![]() .
.
![]() ,
,
![]()
![]()
Решение уравнения
![]() ,
действительно, принадлежит интервалу
.
Теорема Ролля выполняется.
,
действительно, принадлежит интервалу
.
Теорема Ролля выполняется.
2.20 Для
данной функции
и отрезка
найти точку
![]() такую, что
такую, что
![]() ,
или показать, что такая точка существует.
,
или показать, что такая точка существует.
![]() ,
,
Решение.
В данном
случае
![]()
![]() .
.
Равенство принимает вид:
![]() .
.
Получаем уравнение
![]() .
Покажем, что оно имеет корень на интервале
.
Покажем, что оно имеет корень на интервале
![]() .
Обозначим
.
Обозначим
![]() .
Так как
.
Так как
![]()
![]() ,
то по свойствам непрерывных функций,
функция
,
то по свойствам непрерывных функций,
функция
![]() имеет ноль на интервале
,
и данное равенство выполняется в этой
точке.
имеет ноль на интервале
,
и данное равенство выполняется в этой
точке.
3.20 Используя теорему Лагранжа, доказать неравенство при указанных значениях переменной x.
![]()
Решение.
Пусть
![]() .
По теореме Лагранжа для функции
.
По теореме Лагранжа для функции
![]() ,
,
![]() ,
существует точка
,
существует точка
![]() ,
такая что верно равенство:
,
такая что верно равенство:
![]() ,
т.е.
,
т.е.
![]() .
.
Так как функция
![]() возрастает на отрезке
возрастает на отрезке
![]() ,
то она принимает минимальное значение
в точке
,
то она принимает минимальное значение
в точке
![]() .
Поэтому
.
Поэтому
![]() или
или
![]() .
.
Пусть теперь
![]() .
Применим теорему Лагранжа к функции
на отрезке
.
Применим теорему Лагранжа к функции
на отрезке
![]() .
Тогда для некоторого
.
Тогда для некоторого
![]() имеем
имеем
![]()
Поскольку –x
здесь величина положительная, а
достигает максимального значения при
![]() ,
то
,
то
![]() или
или
![]() .
.
Таким образом, при
опять получим
![]() .
.
При
имеем
![]() ,
т.е. неравенство тоже выполняется.
,
т.е. неравенство тоже выполняется.
4.20 С помощью правила Лопиталя вычислить следующие пределы:
а) ; б) .
Решение.
а)
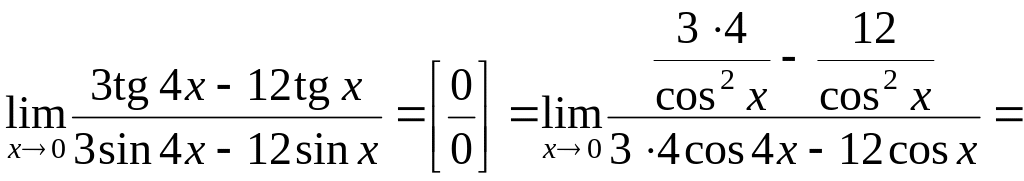
![]()
![]() .
.
б)

![]() .
.
5.20 Установить вид неопределенности в данных пределах. Преобразуя имеющиеся неопределенности к виду или , вычислить пределы с помощью правила Лопиталя.
а)
;
б)
;
в)
![]() .
.
Решение а)
Имеем неопределенность вида
![]() .
Преобразуем ее к виду
.
Получим
.
Преобразуем ее к виду
.
Получим
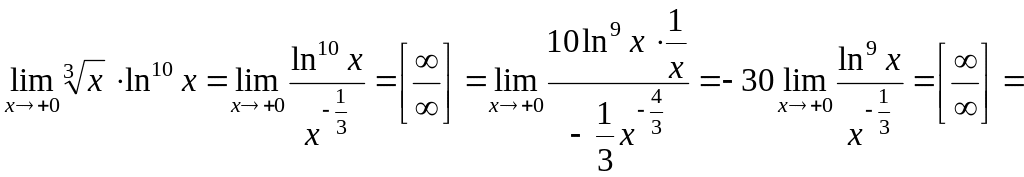

Продолжая этот процесс далее, применив правило Лопиталя ещё 7 раз, получим


б) Имеем
неопределённость вида
![]() .
Преобразуем её к виду
и далее используем асимптотическую
формулу
.
Преобразуем её к виду
и далее используем асимптотическую
формулу
![]()
![]()
![]() при
при
![]() .
Получим
.
Получим
![]()
![]() .
.
Так как
![]() ,
,
![]() ,
,
то исходный предел
равен
![]() .
.
в) Имеем
неопределённость вида
![]() .
Воспользуемся основным логарифмическим
тождеством:
.
Воспользуемся основным логарифмическим
тождеством:
![]() .
.
Тогда
 .
.
Так как
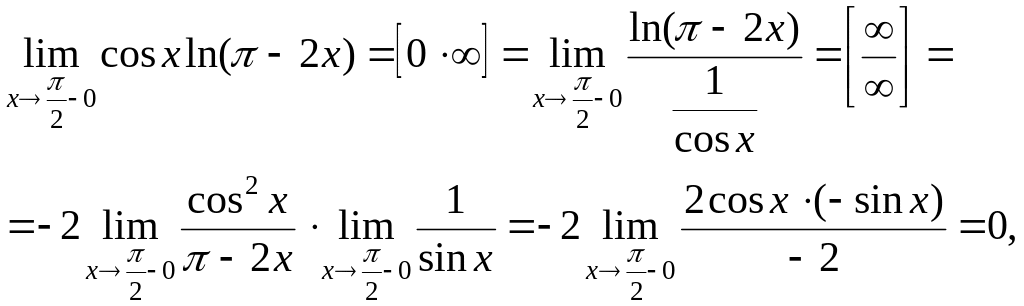
то исходный предел
равен
![]() ,
то есть 1.
,
то есть 1.
Лабораторная работа № 16
Приложения дифференциального исчисления
Необходимые понятия и теоремы: монотонные функции, критерий монотонности функции, точки локального и глобального экстремума функции, необходимые и достаточные условия существования локального экстремума.
Литература: [1] с. 261 – 266, [4] с. 317 – 327.