- •Начала квантовой химии и строение молекул
- •Решаемые задачи:
- •Модель Томсона (1904 г.)
- •Взаимное расположение электронов в атоме
- •Х. Гейгер и е. Марсден (1906-1909 г.)
- •Планетарная модель атома:
- •Серия Бальмера в спектре атома водорода (снизу указаны длины волн соответствующих линий в нм).
- •II. Способность атома поглощать и испускать излучение подчиняется закону, по которому излучение, связанное с переходом, должно быть монохроматическим и иметь частоту ν, определяемую соотношением
- •Зависимость силы анодного тока в цепи от ускоряющей разности потенциалов eVа.
- •Некоторые допустимые решения волнового уравнения для одномерных колебаний натянутой струны.
- •УравнениеШредингера
- •Решение уравнения Шредингера для простейших модельных систем
- •Квантовое число m может принимать значения
- •Спиновые квантовые числа некоторых элементарных частиц и атомных ядер.
- •Физический смысл квантовых чисел электрона
- •1. Размеры орбитали.
- •2. Энергию электронов, находящихся на орбитали.
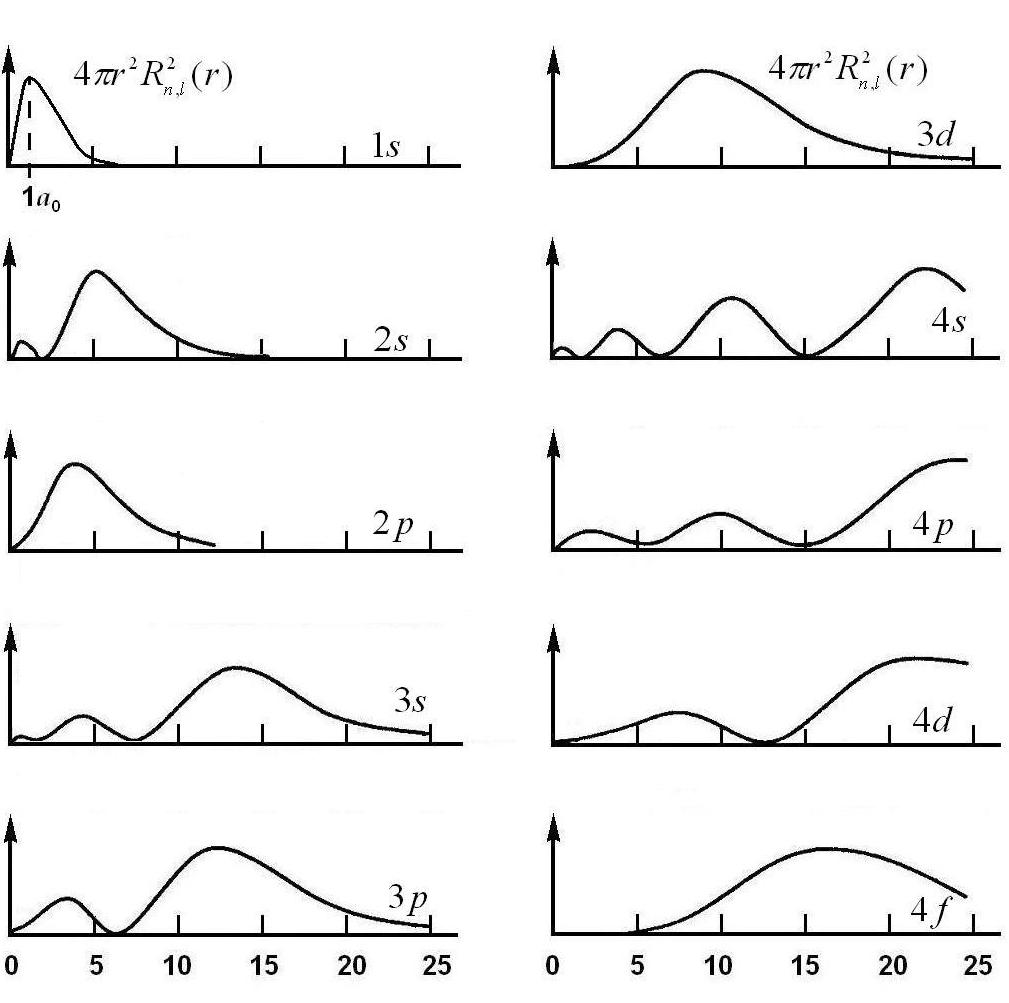
- •Радиальное распределение для орбиталей атома водорода.
- •Теория и методы описания химической связи и строения молекул Метод валентных связей
- •В молекуле н2.
- •Зависимость полной энергии молекулы водорода от межъядерного расстояния
- •Результаты теоретических и экспериментальных определений энергии и длины связи в молекуле н2
- •Основные принципы метода
- •1. Перекрывающиеся ао должны иметь близкие энергии.
- •2. Взаимодействующие ао должны перекрываться в значительной области пространства.
- •3. Ао должны обладать одинаковыми свойствами симметрии относительно оси связи в молекуле.
- •Изменение значений scc в зависимости от межатомного расстояния с─с
- •Водородоподобные.
- •Слетеровские функции (sto).
- •Гауссовские функции (gto). Наименьшие базисные наборы, обеспечивающие описание
- •Число кулоновскихинтеграллов для молекуле пропана, возникающих в различных методах расчета.
- •Сравнительная характеристика полуэмпирических методов.
- •Indo – Intermediate Neglect of Differential Overlap – частичное пренебрежение дифференциальным перекрыванием.
- •Симметрия молекулярных систем Элементы и операции симметрии
- •Оси и плоскости симметрии куба
- •Плоскости симметрии на примере комплексного иона [CuF4]─.
- •1. Правило соответствия
- •2. Правило ассоциативности группового умножения
- •Квантово-химическое описание реакций Квантовая теория химических реакций Понятие о поверхностях потенциальной энергии.
- •Симметрия и относительная энергия мо бутадиена (а) и этилена (б).
- •Схемы строения переходных комплексов для реакции димеризации этилена и взаимодействия этилена с бутадиеном.
- •Симметрия переходного состояния реакции взаимодействия этилена с бутадиеном
Квантовое число m может принимать значения
0, ±1, ±2, ±3, … ± l.
Полный магнитный момент атома j определяется выражением
|
(6.12.) |
где k = ±1/2 (В. Паули)
Спин - чисто квантовое свойство, недоступное объяснению с позиций классической физики. Эта точка зрения сохранилась до настоящего времени и широко представлена в литературе.
Спиновые квантовые числа некоторых элементарных частиц и атомных ядер.
Спиновое квантовое число s |
Частица |
Спиновое квантовое число s |
Частица |
0 |
Ядра 4He, 12C, 16O |
3/2 |
Ядра 11B, 81Br, 37Cl |
1/2 |
Электрон, протон, нейтрон, ядра 13C, 31P |
5/2 |
Ядра 185Re, 241Pu |
1 |
Фотон, ядра 14N, 2H, |
9/2 |
Ядра 179Hf, 209Bi, |
Физический смысл квантовых чисел электрона
Орбиталью называют область пространства, соответствующую определенному набору квантовых чисел п, l и m, где вероятность нахождения электрона |Ψ|2 составляет 0,9 (90%) или функцию квантовых чисел п, l и m введенную для характеристики электронов без учета их спина.
Главное квантовое число п для реально существующих атомов имеет значения от 1 до 7, которые определяют:
1. Размеры орбитали.
2. Энергию электронов, находящихся на орбитали.
Буквенные обозначения главного квантового числа
-
Численное
значение n
1
2
3
4
5
6
7
Буквенное
обозначение
K
L
M
N
O
P
Q
Орбитальное (азимутальное) квантовое число l определяет момент импульса электрона и форму орбиталей. Зависит от n и принимает целочисленные значения от 0 до (n -1).
Буквенные обозначения орбитального квантового числа
Значение l |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
Обозначение |
s |
p |
d |
f |
g |
h |
i |
k |
l |
m |
n |
o |
q |
r |
Магнитное квантовое число ml определяет ориентацию орбитали в пространстве, которая не может быть произвольной. Может принимать целочисленные значения от –l до +l, включая нуль.
Спиновое квантовое число s определяет направление и величину проекции собственного магнитного момента электрона S на выбранную ось z в единицах постоянной Планка:
|
(6.13.) |
Двум противоположным направлениям проекций соответствуют значения s +1/2 и -1/2.