5.4. Использование дерева решений с применением формулы Байеса

Традиционный подход к анализу проблемы с применением дерева решений и формулы Байеса заключается в том, чтобы организовать элементы проблемы в терминах дерева решений, которое описывает в хронологиче­ском порядке решения, которые ЛПР может принимать, и решения, которые управляются случаем.

Для иллюстрации данных положений вновь обратимся к примеру, приведенному в главе 4 (рис.4.9). Дерево решений имеет два вида вершин: верши­ны выбора решений и выбора случаем. Выбор ЛПР обозначается квадрати­ком, а выбор случая - кружком. Ветви, исходящие из дерева решений пред­ставляют возможности, доступные агенту: исходящие из вершин случая со­ответствуют неконтролируемым событиям. Каждой вершине случая приписывается условная вероятность события, представленного ветвью, обуслов­ленной значением полезности в этой вершине.

Листья дерева несут численные значения полезности, связанной со сценарием (путем), ведущим к каждой вершине или, эквивалентно, полезностью ситуации, созданной последовательностью событий, ведущих к листу. Цель нахождения оптимальной стратегии может быть достигнута возвратным анализом: начиная от листьев и перемещаясь последовательно к корню, мы помечаем каждую вершину полезностью ситуации, которую она представля­ет. Каждая вершина случайного выбора помечается ожидаемой полезностью ее последователей, и каждая вершина выбора помечается максимальной по­лезностью ее последователей.

Дерево решений — это эксплицитное представление всех сценариев, возможно проистекающих из данного решения. Вершина дерева представля­ет начальную ситуацию, в то время как каждый путь, исходящий из корня, соответствует одному возможному сценарию. Сценарий включает последовательность действий и наблюдений, выбираемых активным агентом, а так­же наблюдений, сделанных агентом, события, которые могут появиться в окружении агента. Последовательность вершин выражает количественную меру полезности ситуации, создаваемой всем путем. Экспликации проблемы решения в виде дерева облегчает поиск оптимального плана, как предписания реакций на возможные значения наблюдаемых данных.

Рассмотрим следующий пример. ЛПР необходимо принять решение в отношении двух проектов, однако для принятия окончательного решения необходимо произвести дополнительную экспертизу. Пусть t₁ и t₂ — два вида экспертизы, которые необходимо провести ЛПР для окончательного приня­тия решения. Случай, когда ЛПР принял решение вовсе не проводить экс­пертизу, обозначим t_o. Будем выражать затраты и доходы в единицах, со­ставляющих тысячу долларов. Затраты на проведение t₁ равны 5 ед., а затра­ты на проведение t₂ равны 3 ед. Обозначим наши проекты р₁ и р₂- Проект p₁ требует 150 ед. инвестиций, ожидаемый доход — 200 ед., так что в результа­те ЛПР получит прибыль 50 ед. Состояние объекта инвестиций точно не из­вестно, каждый из объектов может находиться в хорошем или плохом со­стоянии. Если объект р₁ находится в плохом состоянии, то может потребо­ваться дополнительно 80 ед. инвестиций, в результате прибыль t от принятия первого варианта составит: 200 - 150 - 80 = -30 (ед.) Проект р₂ требует 120 ед. инвестиций, ожидаемый доход 145 ед., ожидаемая прибыль составит 25 ед. В случае, если объект р₂ находится в плохом состоянии, дополнительные инвестиции составят 20 ед., таким образом ЛПР получает прибыль

145 - 120 -20 = 5 (ед.).

Известно, что шансы в пользу того, что проект р₁ находится в хорошем состоянии, составляют 0,7, для проекта р₂ — 0,8. Тогда ожидаемый денеж­ный доход (EMV) для проекта 1 равен 0,7x50 + 0,Зх(-30) = 35 - 9 = 26 (ед.), а в случае проекта р₂:

0,8x25 + 0,2x5 = 21 (ед.).

Если объект p₁ находится в хорошем состоянии, то экспертиза по проекту Pi даст заключение, что объект инвестиций находится в хорошем состоянии с вероятностью 0,90. Если объект р₁ находится в плохом состоянии, то веро­ятность, что экспертиза обнаружит это, составляет 0,7. Если р₂ находится в хорошем состоянии, то вероятность, что экспертиза установит это, составля­ет 0,8, если же объект находится в плохом состоянии, то это будет установ­лено е вероятностью 0,75.

Дерево решений, соответствующее этой ситуации, показано на рис. 5.3. Дерево организовано в хронологическом порядке выполненных решений и той информации, которая становится доступной. На дереве отражены выбор (тестирование или отсутствие тестирования), изучение результатов тестиро­вания выбранного проекта и, наконец, оценка фактического состояния объ­екта, его стоимости и ожидаемой прибыли.

Чтобы вычислить оптимальную стратегию, мы должны приписать вероятность каждому ветвлению диаграммы. Вероятности ветвей t_o легко под­считать в случае отсутствия теста мы можем просто использовать априорные вероятности с₁ и с₂. Экспертиза h₁ проверяет состояние объекта q₁ Если q₁ находится в хорошем состоянии (обозначим q₁¹), тогда с вероятностью 0,9 тест подтвердит это. Другими словами, с вероятностью 0,1 экспертиза отвергнет проект, в то время как в действительности он является хорошим. Обозначим решение h₁¹ признать объект 1 хорошим, решение h₁⁰ — при­знать объект плохим. ЛПР знает, что априорная вероятность p(q₁^l) = 0,7, p(q₂^l) ⁼ 0,8. Если объект 1 в плохом состоянии, то экспертиза с вероятностью 0,7 отвергнет его. Таким образом, матрица условных вероятностей p₁{h₁^k / q₁^l), где к = 0,1, l=0,1, равна

Для объекта 2 соответствующая матрица р²( h₂^k / q₂^e) имеет следующий вид:

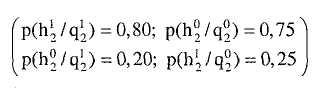
Рис 5.3. Дерево решений с вероятностями на дугах

и метками полезности на вершинах

Однако для того, чтобы приписать вероятности альтернативным разветвлениям случайного выбора вдоль ветви t₁, нам необходимо знать безуслов­ные вероятности p(h₁¹), p(h₂), а также апостериорные вероятности p(q₁ / h₁¹), p(q₁ / h₁⁰), p(q₂ / h₁¹), p(q₂ / h₁⁰) Поскольку эти вероятности не заданы экс­плицитно, мы можем использовать правило Байеса и вычислить p(h₁¹, q₁¹) = p(h₁¹ / q₁¹) x p(q₁¹) = 0,63. Однако для того, чтобы приписать вероятности альтернативным разветвлениям выбора вдоль ветви t₁ нам необходимо знать безусловные вероятности p(h₁¹) так же, как и апостериорные вероятности p(q₁^k / h₁¹), p(q₁^k / h₁⁰), p(q₂^k / h₁¹), p(q₂^k / h₁⁰). Так как эти величины не представле­ны в явном виде, мы вычислим их по формуле Байеса:

P(h₁¹, q₁¹) = p(h₁¹ / q₁¹) x p(q₁¹) = 0,9 X 0,7 = 0,63,

Так как экспертиза применима только к объекту р₁ мы имеем p(q₂¹ / h₁) = p(q₂¹).

Таким же образом мы вычисляем вероятность вдоль ветви t₂, а затем вы­полним процесс возвратного анализа с выбором максимального значения:

• вычислить среднюю полезность для каждой случайной вершины;

• вычислить максимальную полезность в каждом узле после выделения оптимальной ветви;

• проследить отмеченные ветви от корня и вниз, чтобы найти желанный оптимальный план.

Результат применения этой процедуры к дереву показан на рис. 5.3, где стоимость экспертизы вычтена из платежей соответствующих последствий.

Оптимальный план получается прослеживанием от корня к листьям с вы­бором в каждом разветвлении ветви с максимальной полезностью. Опти­мальный план на рис. 2 выделен жирной линией. Он предполагает вложение 5 ед. в проведение экспертизы h₁ затем инвестирование проекта q₁ если имеет место исход h₁ ¹ или инвестирование проекта q₂, если исходом является h₁⁰.

Представление в виде дерева удобно для оптимизации плана, поскольку он содержит эксплицитное описание полной стратегии, т.е. предписание, как действовать в любой мыслимой ситуации. Оно является также концептуаль­но ориентированным представлением, когда мы имеем естественно упорядоченную последовательность решений, которые необходимо принять, при­чем каждое последующее решение обусловлено предыдущими. Однако представление в виде дерева решений часто вступает в противоречие с естественными способами моделирования каузальных отношений в среде. В на­шем примере мы предполагаем, что агент (покупатель) удовлетворен оцен­кой вероятности исхода некоторого теста при условии фактического состоя­ния объекта инвестиций, но не вероятностью того, что качество обусловлено результатами теста (см. рис. 5.4).

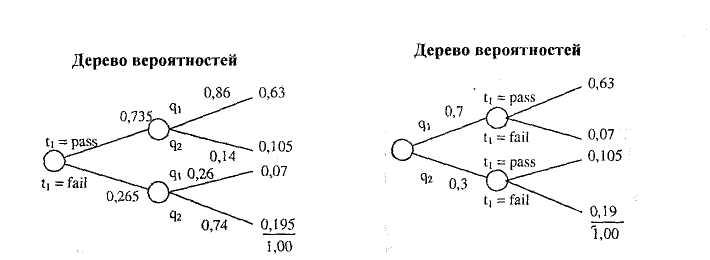
а) Вероятности, необходимые для дерева решений б) Дерево вероятностей,

представленное агентом

Рис. 5.4. Вероятностное дерево

По этой причине аналитик решений находит более удобным обеспечить доступ к вероятностям, используя механизм, называемый вероятностным деревом, а затем преобразовать это вероятностное дерево в дерево решений, используя байесовское правило.

Заметьте, что вероятностное дерево, показанное на рис. 5.4 (б) соответст­вует раскрытию единственной связи с₁ t₁ в представлении байесовской сети. В общем случае проблема вывода вероятностей, необходимых для представления в виде дерева решений — это в точности задача, обрабаты­ваемая формализмом байесовской сети. Таким образом, каузально организо­ванная сеть уверенности может быть использована как база фундаменталь­ных знаний, которая запрашивается, когда возникает необходимость полу­чить параметры для временного построения дерева решений. Два компонен­та знания: знания относительно уверенностей и знания относительно дейст­вий интегрируются в формализации, называемой диаграммой влияния.