5.3. Подход «среднее-дисперсия». Модель Марковитца

Возможно, наиболее широко распространенным подходом к выбору портфеля сегодня является подход «среднее—дисперсия», предложенный Гарри Марковитцем в 1952 году. Основная идея модели Марковитца заключается в том, чтобы рассматривать будущий доход, приносимый финансо­вым инструментом, как случайную переменную, то есть доходы по отдель­ным инвестиционным объектам случайно изменяются в некоторых пределах. Тогда, если неким образом определить по каждому инвестиционному объек­ту вполне определенные вероятности реализации, можно получить распре­деление вероятностей получения дохода по каждой альтернативе вложения средств. Для упрощения модель Марковитца полагает, что доходы по аль­тернативам инвестирования распределены нормально.

По модели Марковитца определяются показатели, характеризующие объ­ем инвестиций и риск, что позволяет сравнивать между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций.

В качестве масштаба ожидаемого дохода из ряда возможных доходов на практике используют наиболее вероятное значение, которое в случае нормального распределения совпадает с математическим ожиданием.

В основе модели Марковитца выбор портфеля представляется следую­щей проблемой оптимизации:

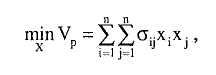(5.1)

или эквивалентно:

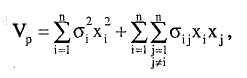
при ограничениях:

(5.2)

(5.3)

(5.4)

где n — число доступных ценных бумаг, х_i — часть портфеля, содержащаяся в ценных бумагах вида i, R_i = E(r_i) — ожидается величина дохода по ценным бумагам i, R_p = E(r_p) — целевой уровень ожидаемого дохода портфеля (²); ² — дисперсия дохода по ценным бумагам i, ² — дисперсия дохода по ценным бумагам вида i, _j— ковариация дохода по ценным бумагам i и j, V_p — дисперсия дохода портфеля.

Эту задачу мы называем задачей квадратичного программирования или QP. Цель состоит в том, чтобы минимизировать риск или дисперсию V_p все­го портфеля при условии получения минимально приемлемого уровня дохо­да R_p при ограничении (5.2). Ограничение (5.3) обеспечивает то, что доступ­ные средства размещаются полностью, и n — неотрицательные ограничения (5.4) обеспечивают то, что и положительные или нулевые инвестиции осуществляются в каждый вид ценных бумаг. Если короткие сделки были допустимы для некоторого подмножества ценных бумаг, то ограничения неотрицательности для этих видов ценных бумаг могут быть опущены. Целевая функция (5.1) является квадратичной, а ограничения — линейными. Суще­ствует несколько алгоритмов для решения этой задачи.

Риск портфеля обычно представляется посредством стандартного откло­нения _р, которое является корнем квадратным из дисперсии и является монотонно возрастающей функцией V_p. Когда R_p изменяется параметрически, решение модели QP получается как множество эффективных точек, представляющих портфели, со свойством минимальности V_p, и таким образом минимальности _р для данного ожидаемого дохода или эквивалентно мак­симальному доходу при данном уровне _р. Это так называемые эффективные портфели. Альтернативная формулировка оптимизации риска-дохода следующая:

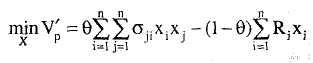
при ограничении

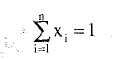
В этой формулировке 0 — взвешивающий параметр. Когда это QP, проблема решается для каждого 0 в интервале от 0 до 1, порождается полное множество эффективных точек.