Эффективная граница

Множество эффективных точек определяет линию, называемую эффек­тивной границей (рис. 5. 2).

Рис. 5.2. Эффективная граница риск/доход

Увеличение совокупности акти­вов, из которых делается выбор портфеля, никогда не сказывается на нижней части границы, поскольку новые ценные бумаги всегда могут быть включены на нижний уровень.

Посредством включения в порт­фель новых активов, доход от которой не имеет активной корреляции с доходом от дру­гих активов, инвесторы могут улучшить значение показателя риска дохода.

Это объясняет текущую тенденцию в направлении глобальных инвести­ций и включение недвижимости и других нетрадиционных активов в порт­фель основных институциональных инвесторов.

То, какой портфель выбрать из возможных вариантов на эффективной границе будет зависеть от функции полезности инвестора, которая представляет преференции по отношению к риску и доходу. Различные инвесторы, сталкиваясь с идентичными эффективными границами, вероятно выберут эффективные портфели, имеющие немного отличающиеся уровни риска и ожидаемого дохода.

Основная модель Марковитца может быть пополнена дополнительными ограничениями. Например, если определено, что не более чем одна часть F_K портфеля должна быть инвестирована в ценные бумаги к одной или более отраслей, дополнительные ограничения могут быть записана в виде:

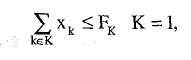
Основная модель Марковитца может породить решение с сотнями видов ценных бумаг, включенных в портфель, некоторые на уровне приближающемся или даже превышающем полное число доступных затрат на таком низком уровне доходности, что их включение в портфель нецелесообразно из-за того, что стоимость транзакций выше дохода от этих ценных бумаг. Следовательно, может оказаться полезным ограничить степень диверсификации. Для этого модель Марковитца может, например, быть дополнена сле­дующими 2n+1 ограничениями:

Здесь у_i — переменные, ограниченные значениями 0 или 1. Задача становится задачей смешанного целочисленного (двоичного) программирования, решение которой требует специальных методов.

Нетрудно включить и линейные стоимости транзакций в модель Марковитца. Для этого стоимость транзакций, связанных с ценной бумагой i, пред­положительно уменьшает ожидаемый доход R_i на _i процентов. Количество ценных бумаг i, уже включенных в общее количество W_i, которое подлежит продаже или покупке, может быть представлено неотрицательными пере­менными х_i⁺ и х_i^-. Для каждой ценной бумаги ограничения добавляются в форме:

и выражение для среднего ожидаемого дохода как:

и подставляется на место каждого из R_ix_i в ограничения (5.2) основной модели.

Бета и индекс модели. Индексная модель шарпа

Если модель Марковитца используется для того, чтобы выбирать из мно­жества ценных бумаг необходимые, то могут возникнуть трудности со сбором данных. Тем не менее, инвесторы успешно используют простые, но эффектив­ные компьютеризированные системы оптимизации по критерию среднее — дисперсия. Они ограничивают решения по размещению инвестиций до не­скольких широких классов, таких как отечественные и зарубежные акции, об­лигации и другие ценные бумаги, путем ограничения секторов экономики.

Шарп разработал практический ответ на проблему расчетов при наличии большого количества ковариаций доходов акций. Его метод требует знания как ковариаций каждого вида ценных бумаг i с индексом I, представляющим рынок, так и бета коэффициент для каждого вида акций. Бета измеряет чув­ствительность доходности ценных бумаг по отношению к индексу доходно­сти и может рассматриваться как наклон прямой линии:

которая называется характеристической линией ценных бумаг.

Значение в этом уравнении может быть в принципе оценено при помо­щи уравнений регрессии на основании исторических данных в виде зависи­мостей доходности ценных бумаг от индекса доходности, с применением индекса и используя уравнение вида:

где _it — ошибка для каждого наблюдения t, представляющая дисперсию в доходности ценных бумаг, не объясняемую дисперсиями рынка. Говорят, что — мера систематического или рыночного риска ценных бумаг. Этот источник риска не может быть уменьшен посредством диверсификации, без снижения ожидаемого дохода, и называется недиверсифицируемым риском.

Часть риска ценных бумаг представляется статистической ошибкой, а именно, отношением суммы квадратов ошибок к дисперсии дохода ценных бумаг. Эта часть называется несистематической, зависящей от компании или диверсифицируемым риском. Эта составляющая риска может быть уменьшена путем диверсификации, так как ошибки коллекции ценных бумаг, суммируясь, имеют тенденцию взаимоуничтожаться.

Другой подход состоит в том, чтобы изучить дисперсию дохода коллек­ции ценных бумаг, которая не объясняется дисперсией индекса доходности. Эта необъясненная дисперсия, представленная как _u², и будет уменьшаться по мере того, как увеличивается число ценных бумаг. Ковариация ошибок ценных бумаг i и j может быть представлена в виде _{ε εj}.

Если каждая из п ценных бумаг составляет равную часть кратную 1/п, не­объясненная ошибка дохода составит величину:

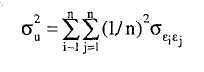
или эквивалентно:

где ² — дисперсия ошибки ценной бумаги i.