Механизм распространения

Предположим, что векторы ихранятся в каждом узле сети, тогда на­ша задача состоит в том, чтобы определить, как влияние новой информации будет распространяться по сети, а именно, как параметры и данного узла могут быть определены из значений и их соседей. Это легко сделать путем нормирования (5.16) и (5.17) по отношению ко всем значениям переменных, которые предполагаются. Например, предположим, что Е является k-м потомком В. Чтобы вычислить k-й сомножитель в произведении (5.18) из значения (Е), мы запишем

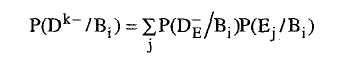
и получим, используя (5.8) и (5.18):

Таким образом, P(D^k-/В_i) получается путем использования -вектора, хранимого в k-м потомке В, и умножения его на фиксированную матрицу условных вероятностей, которые определяют связи между В и Е. Аналогич­но вектор в каждом узле может быть вычислен из значений его потомков путем умножения значений компонент последнего на соответствующую матрицу связей и затем умножения результирующих векторов поэлементно, как показано в (5.18).

Каждый сомножитель P(D^k-/B_i) следует рассматривать как сообщение, отправляемое k-й вершиной-потомком В, и если отправляемое сообщение называется Е, оно будет обозначаться _Е (В),

Аналогичный анализ, примененный к вектору , показывает, чтолюбо­го узла может быть вычислен из значения его отца (родительской верши­ны) и значений, ее окрестности (siblings) также путем умножения на соответствующую матрицу связи. Не требуется непосредственной связи с вершинами, входящими в окрестность, поскольку вся необходимая информация уже содержится в родительском узле для целей вычисления значений , этой вершины по формуле (5.18) и может быть направлена вниз запрашивающей вершине — потомку. Это можно показать путем нормирования (В) по всем значениям родительской вершины А:

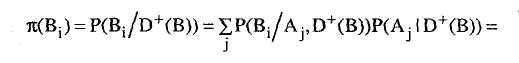
все данные, исключающие D ^- (В)) =

где m изменяется по всем вершинам окрестности В. Выражение в скобках содержит параметры, доступные процессору А, и это выражение, следовательно, можно определить как сообщение _в(А), которое А передает В. Та­ким образом

(5.20)

(5.21)

(5.22)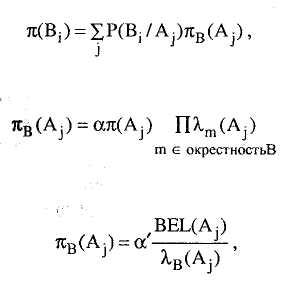

где

или также

Деление на величину _В(А) устраняет из значения BEL(A) вклад D^-_B, как это определяется формулой (5.17).

Эти результаты в целом приводят к следующей схеме распространения возмущения в дереве уверенности:

Шаг 1. Когда процессор В активируется для коррекции его параметров, он одновременно проверяет _в(А)-сообщения, направляемые родительской вершиной А, и сообщения ₁(B), ₂(В), ..., поступающие от каждого из ее дочерних вершин. Используя эти входы, он затем редактирует свои ос и л: следующим образом:

Шаг 2. вычисляется с использованием покомпонентного умножения векторов ₁, ₂,... .

Шаг 3. вычисляется с помощью соотношения:

где — нормализующая константа и _в(А) — последнее сообщение, посылаемое В от родительской вершины А.

Шаг 4. Используя полученные сообщения вместе с редактируемыми значениями и , каждый процессор затем вычисляет новые - и -сообщения, отправленные в систему передачи сообщений для его сыновей и отцов соот­ветственно.

Шаг 5. Распространение «снизу вверх». Новое сообщение _в (А), которое В посылает своей родительской вершине (А) вычисляется следующим обра­зом:

Шаг 6. Распространение «сверху вниз». Новое сообщение _Е(В), которое В направляет; своему k-му сыну Е, вычисляется следующим образом:

или альтернативно.

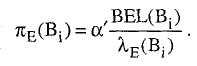(5.23)

Эта схема редактирования показана на рис. 5.9, где умножение любых двух векторов выполняется покомпонентно.

Разумеется, нет необходимости нормализовать -сообщения до их передачи (в действительности только сообщенияВЕL(^.) требуют нормализации). Она выполняется единственно в целях сохранения вероятностного смысла этих сообщений. Дополнительная экономия может быть достигнута, если принять, что каждый узел В передает единственное сообщение BEL(B) всем своим детям, и позволить каждому ребенку (потомку) использовать формулу (5.23) для вычисления соответствующего -сообщения.

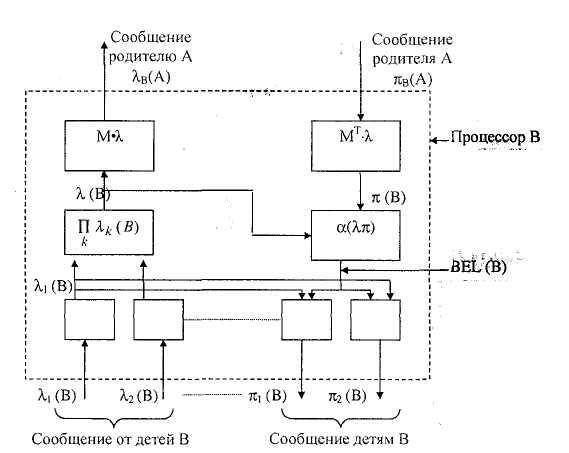
Рис. 5.9. Внутренняя структура одного процессора, производящего

редактирование уверенности для переменной В

Терминальные узлы и узлы данных в дереве требуют специального рассмотрения. Здесь мы должны различать следующие случаи:

(1) Вершины (узлы), находятся в режиме ожидания, они пока не инициированы, т.е. на них еще не поступили входные данные: для таких перемен­ных BEL должно быть равным к и, следовательно, мы должны положить = (1,1,….1)

2. Узлы данных, переменные инициированы значением: следуя форму­ лам (5.16) и (5.17), если верно, что наблюдалось j-e состояние В, мы полага­ем ==(0,...,0,1,0,...)с 1 нa j-й позиции.

3. Фиктивные вершины, как, например, узел В, представляющие вирту­альные или выводимые (judgmental) сообщения, воздействующие на А: для них мы не определяем (В) или (В), а вместо этого направляем сообщение _в(А) в узел А, где _в (А_i)-k Р(наблюдение /А_i) и k — любая удобная константа.

4. Корневая вершина: граничные условия для корневой вершины устанавливаются приравниванием значения корневой переменной (root) = ап­риорная вероятность значения корневой переменной.

Пример 5.2. Для иллюстрации указанных выше вычислений обратимся к примеру 5.1 и положим, что основываясь на всех данных экспертизы, наша уверенность в выборе наилучшего варианта проекта численно представлена значением (А)=(0.80,0.1,0.1). До получения какой-либо информации об идентификации категории экономических показателей узел В находится в режиме ожидания со значением (В)=( 1,1,1), что также дает _В(А)- (А)=( 1,1,1) и BEL(A)= (A). (B) может быть вычислено по формуле (13) (используя _в(А)= (А) и P(B_i/A_j)=0.8 если i=j), что дает

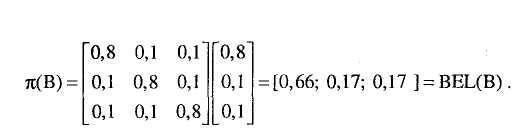
Теперь предположим, что пришли отчеты группы экспертов анализа экономических показателей (виртуальное свидетельство С) в виде сообщения _с(В) = (В) = (0.80,0.60,0.50). Узел В редактирует свою уверенность следующим образом: ВЕL(В) = (В) (В) = (0,80; 0,60; 0,50)(0,66; 0,17; 0,17) =(0,738; 0,142; 0,119) и вычисляет новое сообщение _в(А) для А:

По получении этого сообщения узел А полагает (А)=В(А) и пересчи­тывает свою уверенность по формуле:

BEL(A)= (А)(А) = (0,75; 0,61; 0,54)(0,8; 0,1; 0,1)=(0,84; 0,085; 0,076).

Теперь предположим, что поступили дополнительные данные о низ­ком качестве проекта А₁, в соответствии с которыми соотношение шансов уменьшилось с 0,8 до 0,28, что этот проект будет принят. Чтобы вклю­чить эту информацию во все ранее полученные свидетельства, мы связы­ваем новые виртуальные вершины свидетельств Е непосредственно с А и отправляем сообщение _е(А)=(0,28; 0,36; 0,36) по связи _в(А) в комбина­ции с

и генерирует сообщение:

(5.24)

По получении _в(А) процессор В редактирует свою каузальную поддержку (В) следующим образом:

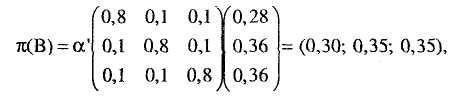
и ВЕL(В) пересчитывается соответственно

ВЕL

Цель распространения уверенности сверху вниз к сенсорным узлам, та­ким как В, двоякая — направить стратегию сбора данных в направлении наиболее информативных сенсорных узлов и обеспечить объяснения, которые оправдывают шаги выводов в системе.

Заметьте, что BEL(A) нельзя взять равным отредактированному априорному значению в А для вычисления ВЕL(В). Другими словами, неправильно редактировать BEL(B) с использованием формулы из учебника:

(5.25)

также известной как формула Джефри, поскольку BEL(A) сама по себе подвержена воздействию информации, передаваемой от В, и, отражая эту информацию обратно к В, мы учитываем одно и то же свидетельство дважды.

На рис. 5.11 показаны 5 последовательных стадий распространения уве­ренности в простом бинарном дереве.

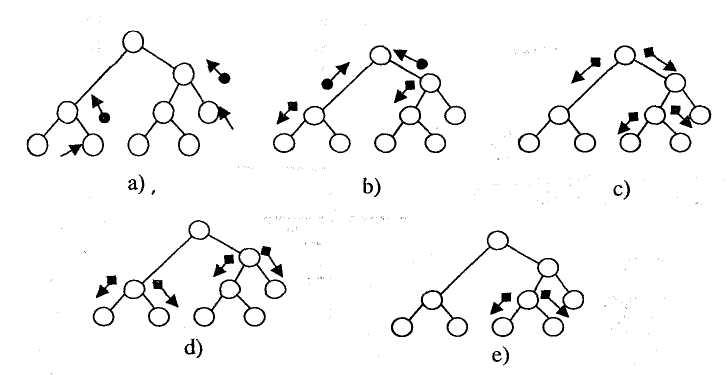
Рис 5.11. Воздействие новых данных, распространяющихся в дереве в процессе передачи сообщений

Вначале дерево находится в равновесии, все терминальные вершины находятся в режиме ожидания. Как только два узла данных активированы, рис. 5.11 -а, круглые маркеры перемещаются по их связям в направлении их роди­тельских вершин, и квадратные черные маркеры в направлении их детей (5.11-b).

В следующей фазе родительские вершины, активированные этими маркерами, поглощают их и производят соответствующее число маркеров для своих соседей (рис. 10-с): круглые маркеры для своих родительских вершин и квадратные маркеры для детей. Связи, по которым поступают абсорбируемые мар­керы, не получают новых маркеров, отражая тем самым тот факт, что на -сообщения не влияют-сообщения, поступающие по той же связи.

Корневая вершина получает теперь два круглых маркера, по одному от каждого из ее потомков. Это приводит к порождению двух квадратных маркеров в направлении «сверху вниз» (рис. 5.11-е).

Процесс продолжается таким образом, пока наконец после пяти циклов все маркеры не будут поглощены, и сеть достигнет нового состояния равно­весия (рис. 5.11-d, e). Как только узлы-листья отправят маркер для своих ро­дителей, они готовы получить новые данные, и когда это происходит, новый маркер посылается в связь, заменяя старый. Таким образом, сеть вывода мо­жет отслеживать поступающие извне данные.