Эффективное вычисление функции уверенности

По мере того как число элементов в Θ увеличивается, происходит экспоненциальный рост времени, необходимого для вычислений, что связано с необходимостью перечисления всех подмножеств данного множества. Рассмотрим прием, который позволяет уменьшить время в схеме D - S до полиномиального. Этот прием реализуется в виде следующих трех шагов. Пусть элементы Θ представлены тройкой (объект, наименование свойства, значе­ние свойства).

Шаг 1. Для каждой тройки (т.е. гипотезы синглетона) скомбинируем параметры, подтверждающие гипотезу. Если s₁, s₂... s_k представляют раз­личные степени поддержки, проистекающие из к правил, поддерживающих один синглетон, тогда комбинированная поддержка есть 1 - (1- s₁),(l— s₂)...(1- s_k). Формула, приводимая здесь, легко может быть получена и идентична функции комбинирования в модели, использующей фактор уве­ренности CF.

Аналогично для каждого синглетона скомбинируем все бпв, представ­ляющие правила, опровергающие этот синглетон. Та же функция комбини­рования, которая используется для этих вычислений и соответствующие численные значения уверенности могут просто быть связаны с отрицанием гипотезы синглетона: не обязательно перечислять все элементы множества размерности п-1 (где п — размерность Θ), которые соответствуют дополне­нию рассматриваемой гипотезы синглетона. Таким образом, все свидетель­ства, подтверждающие синглетон, собираются и представляются при помо­щи бпв и все свидетельства, опровергающие синглетон (подтверждающие гипотезу, соответствующую множеству дополнения синглетона), представ­ляются другим бпв.

Таким образом, мы имеем 2n бпв, половина из которых приписывает уверенность гипотезе синглетона и 0, а другая половина приписывает уверенность отрицанию гипотезы синглетона и Θ.

Шаг 2. Для каждой тройки скомбинируем бпв, полученные на шаге 1, таким образом, как это было описано ранее. Каждой из n гипотез синглетонов приписывается бпв. Каждое бпв приписывает уверенность гипотезе синглетона, ее дополнению и Θ и приписывает нуль всем другим гипоте­зам.

Шаг 3. Конечная задача объединяет бпв из шага 2 в единую оценку уве­ренности по формуле, которую предложил Барнетт. Поскольку эти формулы позволяют вычислять уверенность для синглетона А и для его отрицания А, может быть вычислен интервал уверенности для каждой гипотезы

Мы предполагаем, что эксперты, которые участвуют в конструировании большой базы знаний, могут определить строгую иерархию гипотез, относи­тельно которых система будет получать сведения. Часто признаки или дан­ные связаны как с определенными категориями проблемных ситуаций, так и с отдельными типовыми ситуациями. Пусть множество Ф подмножеств Θ является разбиением Θ. Случайная переменная X ассоциирована с Ф, если два различных исхода в Θ принадлежат одному и тому же множеству Р в Ф, когда им соответствует одно и то же значение X.

Лемма 1. Пусть X₁,..., Х_n — случайные переменные, определенные на конечном пространстве отсчетов Θ и пусть— вероятностное распределение на конечном пространстве отсчетов Θ и такое, что Р()>0 длявсех  Θ. Если X₁ ... Х_n — условно независимы при данных X, тогда Ф₁,. . Ф_n — качественно условно независимы при данном Ф, где Ф — разбиение, связанное сХ и Ф₁ —разбиение, связанное cX_i, i =1,2,...п.

Качественная условная независимость важна для функции уверенности из-за того, что она используется при определении обстоятельств, при кото­рых мы получаем правильный ответ, когда мы применяем правило Демпстера, основанное на разбиении дерева, а не на более тонком разбиении фрейма. Это выражается технически в том, что Веl₁ и Bel₂ поддерживаются Ф₁ и Ф₂

соответственно и

тогда

Ненаправленнаясеть есть пара (J,E) где J— узлы сети— конечное множество и Е — связи сети — множество неупорядоченных пар различ­ных элементов из J. Мы говорим, что элементы i, j являются смежными или соседними, если (i, j)  E. Сеть является деревом, если она связна и в ней отсутствуют циклы. Пусть— дерево. Если дана любая вершина i в J, удаление i из J и удаление всех вершин, инцидентных i из Е по­рождает лес из к поддеревьев. Обозначим коллекцию узлов в j-том подде­реве α_j (i).

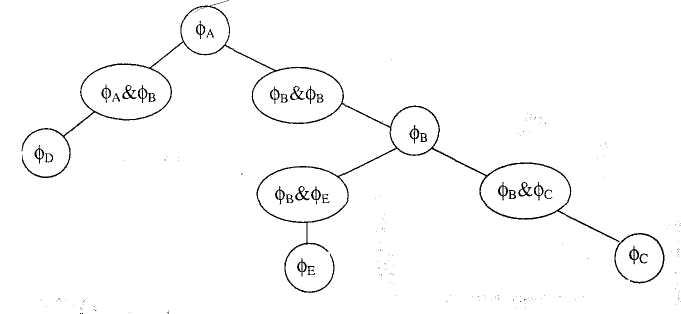
Рис.9.7 Качественное марковское дерево, построенное из причинного дерева на рис. 9.6

Определение: Пусть— конечная коллекция разбиений и пусть

— дерево. Мы говорим, что { Ф_j 1 j  J} есть качественное марковское (разбиение) по отношению к Т или эквивалентно, что T-качественное марковское дерево дляесли для любого i в J, наиболее общие измельчения разбиений в α_т (i) для т = 1,...к — качественно условно незави­симы, при данном разбиении Ф_i, т.е.

Используя Лемму 1, мы можем показать, что байесовское причинное дерево становится качественным марковским деревом, если мы свяжем с каждой вершиной В разбиение Ф_B, ассоциированное со случайной пере­менной, соответствующей В. Оно остается качественным марковским де­ревом, если мы интерполируем между каждой дочерней вершиной и ее ро­дительской вершиной, соответствующей общему измельчению этих двух вершин. На рис.9.7 показан результат интерполяции причинного дерева (рис.9.6).

Качественное марковское дерево может быть построено из диагностиче­ского дерева. В самом деле, если {A}  Sa— семейство в диагностическом дереве, тогда {А } и S_A — разбиение Θ. Качественное марковское дерево имеет узел для каждого из этих разбиений и оно имеет связь между { А }  S_A и { В }  S_B, когда В — потомок А.

Рис.9.8 показывает качественное марковское дерево, которое сконструи­ровано из диагностического дерева (рис.9.6). Самое верхнее семейство со­стоит просто из дочерних вершин 0, 0 не включено, так как оно является пустым множеством. Качественное марковское дерево идентифицируется

таким образом и остается качественным марковским деревом, если {А, А } интерполируется между {A}  S_A и семейством, в котором А является по­томком.

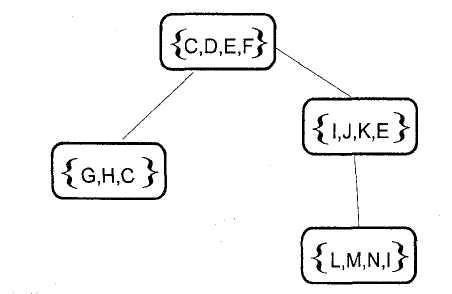
Рис.9.8. Качественное дерево Маркова

Мы можем также связать {А, А } с семейством А, если А — терминаль­ный элемент. Рис.9.9 показывает качественное марковское дерево, которое является результатом, когда такие дихотомии добавляются к рис.9.9.

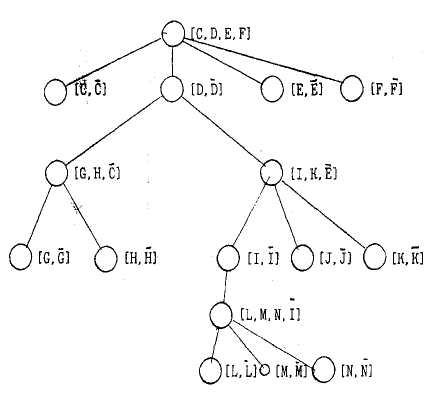
Рис.9.9. Расширенное качественное марковское дерево