9.2. Меры неопределенности в иис

В ИИС обычно имеется механизм сравнения описания ситуации и ме­ханизм применения правила. Механизм сравнения определяет, какие пра­вила являются релевантными в данной ситуации, сравнивая информацию в рабочей памяти с условиями применения каждого правила в базе зна­ний и выписывания правил, условия применимости которых выполняются. Затем аппликатор правила выбирает релевантное правило, которое должно быть применено. В случае, когда оказывается возможным приме­нить несколько правил, аппликатор выбирает и применяет специфическое правило согласно некоторой эвристики, называемой «стратегия разреше­ния конфликтов».

Существуют две основных точки зрения на оценки вероятности, приме­няемые в экспертных системах: объективистский и субъективистский под­ходы. Согласно объективистскому подходу вероятность— это отношение появлений некоторого события к его наблюдениям в терние длительного периода времени. Другими словами, закон больших чисел гарантирует, что при наличии достаточных наблюдений процент появления событий будет приближаться к объективной вероятности.

Персоналистическая, субъективистская или основанная на суждениях оценка вероятности исходит из того, что вероятностные меры уверенности представляют собою уверенность, которую индивидуум имеет относительно истинности некоторого конкретного предложения. Эта точка зрения постули­рует, что индивидуум действует некоторым «разумным» образом, что не исключает, однако, возможности того, что два разумно действующих инди­видуума, столкнувшись с одними и теми же данными, могут иметь разную степень уверенности в одном и том же высказывании.

Пусть А — событие в мире. Собрание всех возможных элементарных со­бытий Ω. называется пространством событий. Вероятность события А обо­значается р(А). Предположим, что В есть другое событие. Вероятность того, что А появится при условии, что В появилось, запишем в виде р(А/В). Р(А/В) называется условной вероятностью А при условии В. Вероятность того, что появятся как А, так и В — р(АВ), называется :овместной вероят­ностью А и В. По определению условная вероятность р(А/В) равна отноше­нию совместной вероятности р(АВ) к вероятности В, т.е.

Таким образом, рассуждая аналогично относительно В, р(АпВ) = р(В/А) Р(А).

Так как

Если события независимы, мы имеем

Другими словами, если А и В несвязные множества,

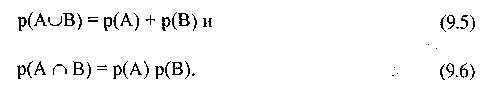
Используя то, что В можно записать как

Переходя от обозначений множеств к вероятностям, комбинируя, полу­чим:

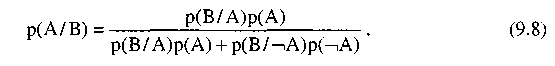
Равенство (9.8) закладывает основу для использования вероятности при оценке неопределенности. Оно обеспечивает способ получения условной вероятности В при условии А. Рассмотрим случай, в котором все правила в ИИС выражены в форме «Если <h -истинно>, тогда <х будет наблюдаться с вероятностью р>». Ясно, что если h наблюдается, правило констатирует, что веро­ятность того, что событие х появится, равно р. Но если статус h неизвестен, и х наблюдается? Равенство (9.8) говорит нам, как вычислить вероятность того, что h истинно и в этом случае. Переход от А и В к h их не случаен. При по­мощи равенства (9.8) мы оставляем общую теорию вероятности и начинаем анализировать вероятностное исчисление в ИИС. Таким образом мы можем перефразировать уравнение (9.8) в терминах гипотез и свидетельств:

Равенство (9.9) связывает гипотезы с квантами подкрепляющих их свидетельств. Интерпретация равенства (9.9) предполагает определение априорной вероятности гипотезы h, p(h) как вероятности, приписываемой h до на­блюдения всяких свидетельств, а также вероятности свидетельств при условии гипотезы.

В ИИС требуемые для решения проблемы вероятности обеспечиваются специалистами-экспертами и хранятся в базе данных. Эти вероятности включают априорные вероятности для всех возможных гипотез р (h) и ус­ловные вероятности для наблюдаемых порций свидетельств при условии гипотез p(x/h).

При наличии одного свидетельства и многих взаимно исключающих и исчерпывающих гипотез:

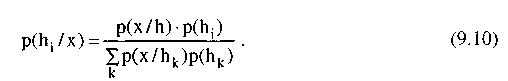
При наличии многих свидетельств, многих взаимно исключающих и ис­черпывающих гипотез, вероятность некоторой гипотезы h оценивается сле­дующим образом:

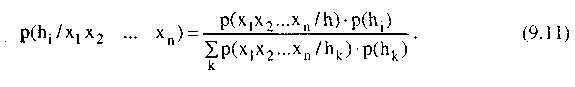
К сожалению, равенство (9.11) требует, чтобы были известны все воз­можные комбинации свидетельств для всех гипотез. Это делает байесовское правило практически не работающим. Поэтому часто предполагают услов­ную независимость свидетельств при условии данной гипотезы:

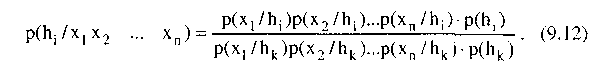
Уверенность может накапливаеться в ИИС системе в результате много­кратного использования правила Байеса для вычисления апостериорных ве­роятностей гипотез при условии наблюдаемых свидетельств. Полученные апостериорные вероятности обеспечивают ранжирование всех потенциально истинных гипотез.

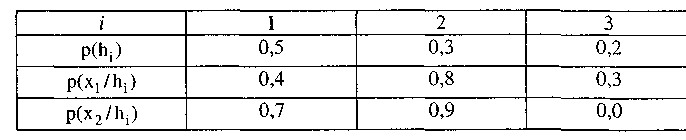
Пример 9.2. Рассмотрим пример, иллюстрирующий этот процесс. Пред­положим, что в некоторой системе три взаимоисключающие и исчерпываю­щие гипотезы h₁,h₂,h₃ имеют априорные вероятности p(h₁), p(h₂) и p(h₃) соответственно. Затем мы наблюдаем два условно независимых фактора х₁ и х₂, которые поддерживают эти гипотезы в различной степени. Таблица 9.2 (показывает условные и априорные вероятности всех гипотез и свидетельств в данном примере).

По мере того как собираются свидетельства, уверенность в гипотезе бу­дет увеличиваться, если свидетельства поддерживают ее, и уменьшаться, если свидетельства противоречат ей. Предположим, что мы наблюдаем вна­чале х₁, а затем х₂. Наблюдая х₁, мы вычисляем апостериорную вероятность гипотезы согласно соотношению (9.10):

Таблица 9.2 Априорные и условные вероятности, используемые в примере 9.2

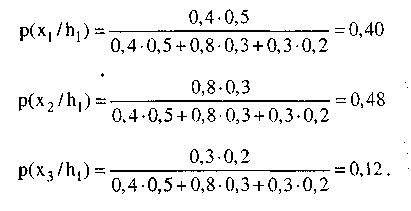
После того как произведено наблюдение х₁ уверенность гипотез h₁ и h₃ уменьшается, в то время как h₂ увеличивается. После наблюдения х₂ мы вы­числяем апостериорную вероятность

Так как x₁ и х₂ — условно независимы при условии гипотезы

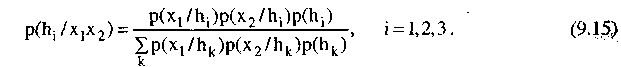
Следовательно,

Хотя первоначальное ранжирование было h₁>h₂>h₃, только hi и h₂ оста­ются для рассмотрения после наблюдения x₁ и х₂, h₂ теперь выглядит более вероятной чем h₁.

Большой объем априорной информации, необходимой для применения правила Байеса, привел к поиску альтернативных методов.

В последующем изложении при применении указанных правил к описа­нию экономических объектов мы будем связывать условно наблюдаемые данные с экономическими показателями, а гипотезы — с некоторыми ситуа­циями. Например, наблюдаемые данные могут быть экономические показа­тели х₁ и х₂ и пусть h — гипотеза о проблемной экономической ситуации, которой соответствуют данные значения этих показателей. Рассмотрим вна­чале пример конечного множества из п элементов. Элементы множества мо­гут обладать одним или более свойствами. Число элементов, которым соот­ветствует показатель х₁ есть n(x₁)=n₁ и число категорий, которым соответст­вуют два показателя одновременно, есть n(x₁ x₂)=n₁₂. Заметим, что имеет ме­сто равенство:

Рассмотрим теперь случай, когда два показателя связаны с гипотезой о ситуации h. Сделаем предположение, что оба эти показателя независимы как в совокупности, так и в подмножестве этой совокупности. Тогда

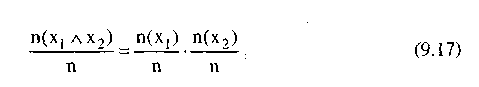
и точно, так же

т.е. принимая относительные частоты за оценки соответствующих вероятно­стей, получим:

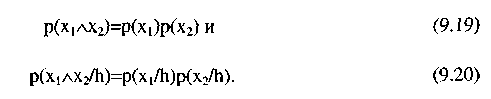
Таким образом в соответствии с теоремой Байеса получим

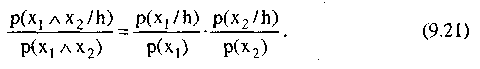
Чтобы показать, как теория Байеса может быть применена к принятию решений об инвестициях, полезно рассмотреть теорему Байеса, используя следующие обозначения:

h: гипотеза h,

h: гипотеза «не h»,

х: свидетельство х,

x: свидетельство «не х»,

p(h): априорная вероятность гипотезы h,

p(h/x): апостериорная вероятность гипотезы h при наличии свидетельств х,

p(h,x): совместная вероятность появления гипотезы h и свидетельства х. По определению, условная вероятность

Подставляя (9.23) в (9.22) мы получаем

Поскольку

Равенство (9.24) может быть преобразовано к виду:

Используя уравнение (9.25), возможно вычислять апостериорную веро­ятность удовлетворения гипотезы h при наличии данных свидетельств из допустимых вероятностных данных

По формуле (9.24) можно вычислить апостериорную вероятность удовле­творения гипотезы h при данных свидетельствах из доступных вероятност­ных данных

Вычисления (9.24) могут быть реализованы использованием понятий шансы и отношением правдоподобия. По определению шансы O(h) и O(h/x) могут быть выражены следующим образом:

Согласно уравнению (9.28) апостериорные шансы могут быть вычислены как произведение O(h) и LR(h/x). Таким образом (9.28) может быть ис­пользовано, чтобы дать численную оценку связи экономических показателей с проблемной экономической ситуацией. Рассмотрим пример 9.3, данные по которому представлены в таблице 9.3.

Эта таблица частот отражает данные о доходности 200 ценных бумаг для различных предприятий. В данном случае в качестве гипотезы h при­нято попадание в группу ценных бумаг с высоким уровнем доходности, гипотеза h — попадание в группу предприятий с низким доходом, сви­детельство х — ценные бумаги принадлежат электронной индустрии, свидетельство х — ценные бумаги принадлежат неэлектронной инду­стрии.

Таблица 9.3

Если нет другой информации о ценных бумагах, априорную вероятность доходности можно оценить следующим образом:

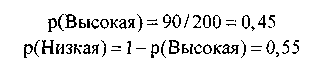
В случае, если отрасль, к которой принадлежит ценная бумага известна, можно применить формулу (9.28) Априорные шансы равны:

Отно­шение правдоподобия равняется:

Таким образом, при наличии свидетельства о том, что ценные бумаги принадлежат электронной отрасли, вероятность получения дохода более 30% увеличивается с 0,45 до 0,8. Предполагая, что существуют дополни­тельные свидетельства относительно того, ориентирована ли продукция на экспорт или на внутренний рынок, дополнительная таблица частот для рын­ка может выглядеть следующим образом:

Таблица 9.4

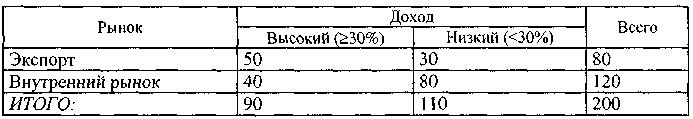
Таким же образом апостериорная вероятность может быть вычислена как:

Таким образом:

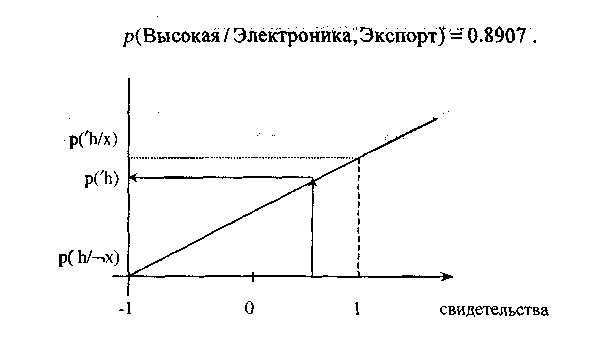
Рис.9.2. График интерполяции значения вероятности в зависимости от свидетельства

Располагая этими двумя элементами свидетельств — отрасль промыш­ленности и экспортная ориентация продукции — мы получаем увеличение вероятности получения более высокого дохода с 0,45 до 0,8907.

До сего времени мы предполагали, что свидетельства известны с полной уверенностью, но это может быть не так во многих случаях. Например, мы полагали, что компании могут быть дихотомизированы по критерию отрасли или рынка, в действительности такие характеристики часто являются вопро­сами степени. Компания может производить 60% своей продукции для элек­тронной индустрии и продавать 50% полного объема выпуска на внешние рынки. Один способ обработки неопределенных свидетельств состоит в том, чтобы применить метод интерполяции. На рис. 9.2 показано, что вероятность можно отобразить в интервал [—1,0,1]. Если положе­ние свидетельств на шкале [—1,0,1] известно, соответствующую вероятность можно линейно интерпретировать. Рассмотрим пример.

Пример 9.4.

Если компания производит 100% продукции для электронной индустрии, _v=1, если компания не продает совсем электронную продукцию, то _v⁼ -1-Если компания продает электронную продукцию в средней пропорции ко всем компаниям электронной индустрии (например, 30%), нормализованная вели­чина _v=0. Предположим, компания производит 60% продукции для элек­тронной индустрии, свидетельства могут быть формализованы следующим образом: _v (Электроника) = (60-30)/(100-30) = 0.43 , следовательно,

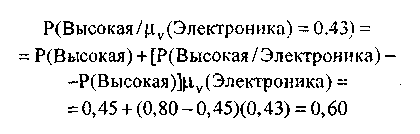
Заметьте, что апостериорная вероятность ослаблена с 0,8 до 0,60 вследст­вие неопределенности свидетельств. Вновь предполагая, что нормализован­ные свидетельства экспорта _v(Экспорт) = 0,5, ослабленная апостериорная вероятность с обоими элементами свидетельств равна:

Рис.9.3. График интерполяции зависимости вероятности от уверенности

В общем случае ценные бумаги могут быть категоризованы и более чем в два класса (например, классы А, В, С и D). Посредством прямого обобщения уравнений (9.22) — (9.25) и уравнения (9.29), в которомобозначает

вероятность удовлетворения гипотезы \ получим:

Самая простая стратегия, включающая многие свидетельства состоит в том, чтобы использовать все свидетельства. Однако эта стратегия неэффек­тивна, поскольку некоторые свидетельства в ретроспективе могут быть на­столько слабыми, что их можно вовсе не учитывать. Таким образом, жела­тельно упорядочить насколько можно более эффективно последовательность применения свидетельств.

Последовательность, в которой применяются свидетельства становится, особенно важной, когда ИИС системы используются интерактивно. Этими полезными средствами упорядочения являются случайное упорядочение, упорядочение по важности и упорядочение по правилам.

Случайное упорядочение. Основное преимущество случайного упорядо­чения — это простота. Однако этот метод может заставить ЛПР иметь дело с тривиальными свидетельствами.

Упорядочение по важности. Упорядочение по важности свидетельств может основываться на опыте инвесторов или экспертов по инвестирова­нию.

Когда времени недостаточно и доступно значительное количество вы­числительных ресурсов, будет оправданно применить подход, основан­ный на правилах, которые упорядочивают свидетельства, используя фор­мулу: .

для свидетельства x_j.

Формула (9.30) представляет сумму апостериорных вероятностей изме­нений, которые могут появиться как результат знания того, являются ли сви­детельства Е_j истинными или ложными.

Система может найти свидетельства такие, что

В формуле (9.30) можно использовать сумму квадратов вместо абсолют­ных разностей. Веса также могут быть применены к гипотезам. Главный не­достаток подхода, основанного на правилах — это большой объем вычисле­ний.