Комбинация функций веры

Сбор данных для подготовки проекта решения требует метода комбинирования оснований для гипотезы или ее отрицания, основанного на многих аккумулированных наблюдениях. CF функция комбинации не дает никакой взаимосвязи между коэффициентами уверенности в двух гипотезах и разли­чается наиболее существенно от правила DST в этом случае. Если даны два бпв, основанные на разных наблюдениях, Демпстер показывает, как вычислить новое бпв, которое представляет результат комбинирования признаков (данных).

Когда текущие свидетельства ведут к нескольким оценкам веры относи­тельно одних и тех же гипотез, веру можно комбинировать, чтобы оценить веру в гипотезу. С этой целью в DST обычно комбинирует различные функ­ции веры путем вычисления их ортогональной суммы в соответствии с пра­вилами Демпстера—Шейфера. Функция комбинирования Демпстера пред­полагает, что m₁m₂ могут быть вычислены из mi, m₂ путем рассмотрения всех произведений m₁ (x) m₂ (у), где х и у — индивидуально варьируются по всем подмножествам Θ. Можно показать, что результирующая функция также будет бпв, т.к. результат суммирования всех таких произведений по определению бпв равен 1 :

Для каждого подмножества А в Θ правило Демпстера определяет m₁ m₂ (А) как сумму всех произведе­ний вида m₁ (x) m₂ (у), где х и у — выбираются из подмножеств Θ всеми возможными способами, такими, что их пересечение принадлежит А.

Предположим, что m₁ и m₂ — два базовых приписывания вероятностей в совокупности событий Θ. Тогда ортогональная сумма есть

где К — константа нормализации

тогда по определению m₁ m₂ (ø) = 0. Если К^-1=0 ортогональная сумма не существует и m₁ и т₂ называют полностью взаимоисключающими. Величина (log К) называется весом конфликта между Ве1₁ и Веl₂. Таким образом, если Belj и Ве1₂ не находятся в конфликте, К=1 и если Bel₁ и Ве1₂ полностью противоречивы К^-1= 0. Ортогональная сумма является коммутативной и ассоциативной.

Пусть Ве1₁ Bel₂ и m₁ m₂ обозначают две функции уверенности и соответствующие им бпв. Правило D - S определяет новую бпв, обозначаемую m₁m₂, которая представляет результирующий эффект от m₁ и m₂. Соответ­ствующая функция веры также может быть вычислена из m₁ m₂ по определению функции уверенности. Величина m(Θ) — это мера или часть общей веры, которая приписана Θ, т.е. которая остается неприписанной после при­своения веры различным подмножествам Θ.

Правило Демпстера констатирует, что бпв, представляющее комбинацию m₁ и m₂, распределяет полное количество веры между подмножествами Θ путем приписывания m₁ (x) m₂ (у) множеству, являющемуся пересечением X и Y. Заметьте, что существует обычно несколько различных подмножеств Θ, пересечение которых дает то же самое подмножество Θ.

Предположим, две функции веры m₁ и m₂ определяются на совокупности событий Θ, как показано в таблице 9.8.

Таблица 9.8

Иллюстрация правила комбинации Демпстера—Шейфера

Тогда

Все другие подмножества Θ имеют свою комбинированную веру, рав­ную 0, и сумма всех комбинированных приписываний вероятностей т₁ т₂ равна 1.

Одна очевидная проблема с DST заключается в сложности вычислений, так как почти все функции требуют исчерпывающего перечисления всех возможных подмножеств пространств событий. Однако если ограничиться гипотезами, которые представлены взаимно исключающими синглетонами и их отрицаниями, то существует линейный по времени алгоритм для вычис­ления Bel, m и других функций DST, необходимых для применения правил Демпстера.

Основные положения теории DST сводятся к следующему:

1. Воздействие свидетельств распространяется на степенное множество 2^Θ множества базовых элементов {Θ} (которые являются полной группой взаимоисключающих событий), называемой фреймом гипотез.

2. Функция вероятности массы (бпв), заключенная в интервале [0,1] приписывается каждому дизъюнктивному подмножеству таким образом, чтобы сумма (или полная вероятность массы) равнялась 1, а вероятность массы, приписанная пустому множеству есть 0, т.е.

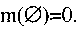
3.Уверенность в конкретных гипотезах А представлена как интервал

где для подмножеств В в А:

Здесь Ве1(А) — вера (или поддержка) А и Р^* (А) — возможность или верхняя граница А. Ве1(А) — таким образом, мера полного количества веры в А и в его подмножества (не количество, приписанное точно А) и Р^* (А) — степень, до которой невозможно сомневаться в А.

4. Свидетельства комбинируются по правилу комбинирования Демпстера (9.58). Для двух свидетельств 1 и 2, где А представляет подмножество гипо­тез, которые поддерживаются первой группой показаний (свидетельств), и В представляет подмножество гипотез, которые поддерживаются второй группой свидетельств (показаний), новая вера в подмножество гипотез С, (m(С)), которое поддерживается как первой, так и второй группой свиде­тельств, определяется как сумма произведений масс, приписанных подмно­жествам А и В, пересечение которых есть С, деленное на фактор нормализа­ции, равный 1 минус сумма произведений масс подмножеств А и В, пересе­чение которых есть пустое множество.

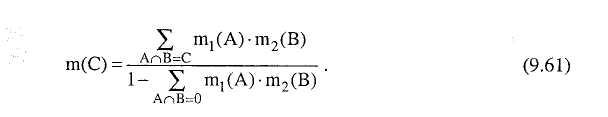
Рассмотрим, например, множество Θ взаимоисключающих гипотез

Один набор данных может говорить в пользу двухэлементного подмно­жества Э, например, {а,b}. Это подмножество соответствует гипотезе, кото­рая является дизъюнкцией ее элементов, т.е. ab. Аналогично гипотеза, со­ответствующая подмножеству {c,d}=cd. Поступившие данные вынуждают эксперта приписать некоторую степень веры в гипотезу {c,d}.

Таким образом, первоначальные данные позволяют приписать некоторую веру обоим подмножествам. Далее новые данные могут помочь эксперту ис­ключить альтернативу «а» до некоторой степени. Данные, ослабляющие «а», эквивалентны данным, усиливающим  а, т.е. гипотезу bcd или подмноже­ство {b,c,d}, однако эта гипотеза ничего не говорит о том, каким образом рас­пределить веру в трехэлементном множестве между гипотезами синглетонов, {b}, {с}, {d}. Каждый элемент в Θ соответствует одноэлементному подмноже­ству, называемому синглетон. Посредством рассмотрения всех возможных подмножеств Θ, 2^Θ, множество гипотез, которым приписывается вера, расширяется. Под термином «гипотеза» мы понимаем гипотезу в расширенном смысле, обозначая любое подмножество исходного множества гипотез в Θ.

Бпв есть обобщение распределения вероятностей, оно приписывает каж­дому синглетону Θ вероятности из интервала [0,1 ] такие, что их сумма рав­на 1.

Используя 2^Θ — расширенную область всех подмножеств Θ, бпв, обозначаемое m, приписывает число из интервала [0,1 ] каждому подмножеству 0, так что их сумма равна 1. По определению число 0 нужно приписать пусто­му множеству, т.к. это множество соответствует ложной гипотезе. Таким образом, m_i приписывает меру (долю 1), основанную на данном свидетель­стве i каждому элементу решетки (рис.9.5), а не только элементам в самом низу (нулям решетки). Как это имеет место и в случае распределения веро­ятностей, величина m(А) — это мера или часть общей веры, приписанной точно А, где А — элемент 2^Θ .

Эта часть веры не может далее поделена между подмножествами А и не включает часть меры, приписанной подмножествам А. Поскольку вера в А несомненно включает веру во все подмножества Θ, содержащие А (т.е. вер­шины выше, принадлежащие фильтру, или элементы фильтра), полезно опре­делить функцию, которая оценивает полное количество меры уверенности для каждого подмножества в Θ. Эта функция, применимая к подмножеству в 2^Θ, А с 2^Θ, будет включать не только веру, приписанную точно А, но и всем под­множествам, являющимся подмножествами Θ. Такая функция, называемая функцией веры в модели D — S, определяется ниже.

Рис.9.5. Решетка подмножеств Θ

Таким образом, Ве1(А) — это мера полного количества уверенности в А, а не количество, приписанное точно А свидетельствами, соответствующими бпв т. Заметьте, что из данных определений вытекают следующие наблюде­ния:

1. Ве1(а) и m(а) — равны для синглетонов, а Θ.

2. Ве1(А), где А — любое подмножество Θ, равно сумме значений m для каждого подмножества в подыерархии, сформированной с использованием А в качестве корня, например, Bel({a,b}) = m({a,b}) + m({a}) + m({b}).

3. Bel(Θ) всегда равно 1, т.к. Bel (Θ) — сумма значений m для всех под­ множеств Θ. Эта сумма должна быть равна 1 по определению бпв. Ясно, что полное количество уверенности в Θ должно быть равно полному количеству уверенности, т.е. 1 т.к. синглетоны образуют исчерпывающее множество событий.

Например, свидетельства в пользу единственного подмножества А могут ничего не говорить относительно веры в другие подмножества. Если m(А) = S и т не приписывает никакой веры другим подмножествам Θ, тогда m(Θ) = 1-S. Таким образом, оставшаяся вера приписывается Θ, а не отрицанию ги­потезы, т.е. А, как это имеет место в модели Байеса.

Рис 9.6. Дерево гипотез