Правила остановки

Следующие факторы могут быть применены в качестве множества пра­вил остановки:

M_u: верхний порог, который вероятность может превосходить;

M_L : нижний порог, который вероятность не может превосходить;

Р_МАХ: максимум вероятности, при которой остающиеся свидетельства являются положительными.

P_M]N: максимум ветроятности, при которой остающиеся свидетельства являются негативными.

Процесс накопления свидетельств целесообразно остановить, когда вы­полняются следующие условия:

1. Если более не осталось свидетельств, сравнить 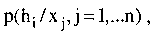и вы­ брать

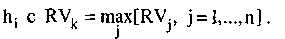
2. Если P(MIN) гипотезыгипотеза h_k является наилучшей альтернативой.

1. Если P(MIN) гипотезы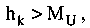то гипотеза h_k выполняется.

Целесообразно исключить гипотезу, которая удовлетворяет следующим условиям.

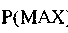4. Если ) гипотезы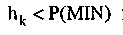 всех 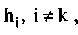гипотеза h_k не подтверждается.

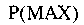5. Еслигипотезы, гипотеза Н_к не подтверждается.

Если ни одно из условий 1-5 не выполняется, необходимо продолжить вывод, т.е продолжить, если:

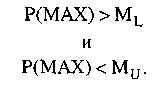
9.3. Модель Шортлифа и Бьюкенена

Высокая трудоемкость подготовки статистических данных, особенно в случае многомерных вероятностных распределений, необходимость работы в условиях редко повторяющихся ситуаций, когда трудно говорить о нали­чии генеральной совокупности или представительности выборки, сделали актуальными попытки замены понятия вероятности некоторыми доступны­ми оценками. Как было сказано выше, статистиками часто используется формула Байеса. Однако полезность формулы Байеса часто ограниченна из-за того, что отсутствуют данные, необходимые для оценки априорных и ус­ловных вероятностей. Шортлиф и Бьюкенен предложили модель, посредст­вом которой можно делать выводы на основе неполных знаний. Эти методы заложены в программы целого ряда экспертных систем, которые делают возможным использование знаний экспертов не экспертами. Здесь игнори­руется тот факт, что данные в действительности собираются «по крупицам», т.е. последовательно.

Метод Байеса требует огромного количества статистических данных, не просто для каждого значения х_к но также для описания взаимосвязей х с каждой ситуацией h_i.

Наибольшая трудность состоит в том, чтобы непосредственно связать гипотезы и соответствующие им признаки. Пытаться извлечь такие взаимосвя­зи из данных аудита фирмы прошлых лет почти невозможно. Кроме того, характер таких взаимосвязей меняется из года в год. Альтернативой сбору исчерпывающих знаний является использование знаний, которые менеджер-эксперт имеет относительно кризисных ситуаций предприятия. В случае ко­гда знания проистекают от эксперта, условные вероятности и их сложные взаимосвязи не обязательно собирать исчерпывающим образом. Вместо это­го могут собираться и обрабатываться мнения, которые можно интерпрети­ровать как вероятности.

Преимущество системы, основанной на правилах экспертов по сравне­нию с системой условных байесовских вероятностей заключается в следую­щем: V возможно использование фундаментальных знаний и закономерностей;

• возможно использование опытного знания для рассмотрения малых групп экономических объектов, имеющих разные классы проблемных ситуаций, для которых нет достаточного статистического материала;

• легкость модификации, поскольку правила не связаны эксплицитно одно с другим, нет необходимости строить заранее структурированное дерево решений;

• изменение правил и добавление новых правил не требует анализа слож­ных взаимосвязей с другими частями системы;

• облегчается поиск потенциальных несовместностей и противоречий в базе знаний;

• могут быть использованы простые механизмы объяснений;

• пользователя можно информировать только о той части процесса, реше­ния, которая ему необходима.

Предложенная Шортлифом и описываемая ниже модель по существу является аппроксимацией условных вероятностей. Если совокупность всех релевантных данных или свидетельств обозначитьгипотеза (проблемная экономическая ситуация), тогда p(h/x) — условная вероятность того, что для наблюдаемого объекта имеет место ситуация h_i в свете свидетельств х, p(h_i/x) может быть вычислена из компонент условных вероятностей:

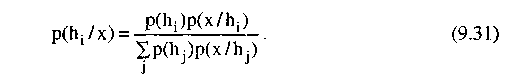
здесь p(h_i) — априорная вероятность гипотезы, например, если всего альтер­нативных гипотез п. p(x/h_i) — вероятность появления значений признака, свидетельств х в пределах объектов класса h_i рис. 9.4 .

Выражение для условной вероятности есть в действительности выражение пра­вила принятия решения или вероятност­ного вывода. Например, выражение p(h_i/x_k)=α можно прочесть как утвержде­ние, что существует 100α шансов, что для наблюдаемого объекта, что при наличии признаков (симптомов) х_к, имеет место гипотеза h_i. Правило может быть сформу­лировано в виде: если объект имеет признаки или сим­птомы х_к, то делаем вывод, что для него справедлива гипотеза h_i с вероятностью α.

Модель Шортлифа и Бьюкенена требует оценки экспертами данных в пользу гипотезы или в пользу ее отрицания. Шортлиф и Бьюкенен ввели понятия: меру уверенности— MB и меру неуверенности— MD для обозначения весомости свидетельств. Эти меры были успешно применены в медицинской диагностической экспертной системе MYCIN, предназначенной для постановки диагноза на основании наблюдаемых симптомов заболевания. Сходство функций, предложенных различными авторами, состоит в том, что степень поддержки фактами всегда пропорциональна разности условной вероятности свидетельства при данной гипотезе и его априорной вероятности: P(x/h)-P(x) или его априорной вероятности отрицания гипотезы: Р(х/h) - Р(х/h).

Кроме того, она обратно пропорциональна условной вероятности свиде­тельства х: чем меньше мы ожидаем встретить такие эмпирические факты, чем меньше их исходная вероятность, тем важнее их наличие.

Знания в ИИС, т.е. правила, относящиеся к сфере профессионального опыта, могут быть выражены, например, в виде правил продукции в сле­дующем виде: «Если А, то — со степенью надежности X — В».

MB[h,x]=α означает, что степень уверенности в гипотезе h, основанная на свидетельстве х, есть α.

MD[h,x]=β означает, что степень или мера неуверенности в гипотезе h, основанная на свидетельстве х, равна β.

Свидетельства х не обязательно являются наблюдаемыми событиями, но могут быть, в свою очередь, гипотезами. Таким образом, мы можем записать MB[h₁,h₂], чтобы указать на меру увеличения уверенности в гипотезе h₁ при условии, что гипотеза h₂ является истинной.

Аналогично MD[h,x] есть мера неуверенности в гипотезе, если гипотеза h истинна. Например, в высказывании «причина того, что доходы падают — низкое качество продукции» MB[h,x]=0,7 согласно простому правилу, сформулированному экспертом. Здесь 0,7 просто отражает степень, с которой эксперт убежден, что h истинно при условии, что х истинно. В то же время, в данном примере MD[h,x] равно 0, так как нет причин увеличивать неуверенность в h на основании х.

В соответствии с субъективной теорией вероятности мы утверждаем, что персональная вероятность гипотезы по оценке эксперта P(h) отражает его уверенность в h в любой момент времени. Таким образом l-P(h) можно рассматривать как оценку неуверенности эксперта относительно истинности п. Если P(h/x) больше, чем P(h), наблюдение х увеличивает уверенность эксперта в h.

Предположим, наоборот, что P(h/x) меньше чем P(h). Тогда наблюдение х будет уменьшать уверенность эксперта в h и в то же время увеличивать его неуверенность в истинности h. Таким образом мы можем определить

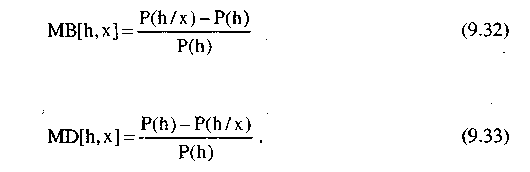
Следовательно мы оцениваем меру увеличения уверенности MB[h,x] в долях неуверенности, считая, что гипотеза h является следствием наблюде­ния х.

Заметим, что одно и то же свидетельство не может выступать как в поль­зу, так и против гипотезы, так что если

Кроме того, возможен случай, когда т.е. гипотезы не зависят

от свидетельств, при этом:

Определим более строго MD и MB с учетом того, что они не могут быть отрицательны.

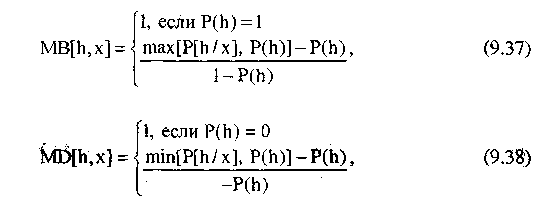
Таким образом,

Шортлиф ввел также коэффициент уверенности:

Таким образом CF объединяет значения MB и MD в одно, причем

Несмотря на то, что CF изменяется от -1 до 1, основная концепция анало­гична байесовскому подходу. В приведенном выше примере CF может быть вычислен следующим образом:

Используя выражения MD и MB через P[h/x], P(h) можно записать

Основные свойства введенных мер уверенности выражающий при помойки следующих соотношений:

Заметим, что эксперт может поддерживать гипотезу со степенью уверен­ности а, но это не значит, что он поддерживает отрицание гипотезы со сте­пенью

уверенности 1-α, т.к. когда х подтверждает h,то

Для комбинации свидетельств в случае, когда неизвестны точные значе­ния априорных и апостериорных вероятностей гипотез, вводятся следующие приближенные методы оценки.

Если x₁ и х₂ соответствуют упорядоченными наблюдениями свиде­тельств, причем Вначале наблюдается х₁, а затем x₂

Аналогичным образом для конъюнкции и дизъюнкции гипотез применя­ются методы, дающие также лишь приближенные значения:

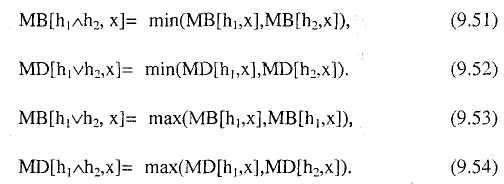
Если истинность или ложность части свидетельств х₁ не известна с пол­ной определенностью, но значение CF (основанного на априорных данных х¹) известно, и оно отражает степень уверенности в х₁, тогда MB¹(h,x₁) и MD¹(h,x₁)— представляют собою степени уверенности и неуверенности в h, когда известно, что х₁ является истинным с полной определенностью, тогда окончательные значения степени уверенности и неуверенности определяют­ся соотношениями:

где х¹ — все имеющиеся данные, MB¹, MD¹ — мера доверия (недоверия) в случае, если известно, что x₁ истинно.

Пример 9.5. Рассмотрим пример выбора одного из двух вариантов инве­стирования проектов в экспертной системе. Пусть мы имеем модель выбора с двумя альтернативными вариантами: реконструкция производства и строи­тельство нового предприятия. При этом в качестве основных факторов, оп­ределяющих выбор, можно было бы условно принять следующие:

1. ожидаемый прирост товарной продукции,

2. ожидаемая прибыль,

3. ожидаемая себестоимость товарной продукции,

4. ожидаемый прирост производительности труда,

5. необходимые прирост численности работающих,

6. ожидаемое увеличение среднегодовой производственной мощности,

7. требуемый объем капиталовложений,

1. требуемый объем капитальных вложений на строительно-монтажные работы,

8. лимит капитальных вложений,

10. фондоотдача,

11. ожидаемые сроки завершения,

12. затраты на обеспечение мероприятий по защите окружающей среды. Предположим далее, что инженер по знаниям провел интервью с ЛПР по значению каждого из факторов x_i, рассчитанному в проекте для обоих ва­риантов, и на основании этого оценил

коли­чественная мера одного из двенадцати приведенных факторов как для одного, так и для другого варианта j = l,2 (реконструкция или новое строительство), здесь h_j,j = l,2 соответственно одна из гипотез.— доля уве­ренности в том, что будет принят вариант h_j на основании данных x_i.

Предположим далее, что инженер по знаниям ввиду большей трудоемко­сти формирования таблиц p(h/x) принял решение собрать опросы ЛПР эмпирического правила, определяющие влияние комбинаций факторов на принятие решения и обобщение этих данных в виде шести правил, которые составляют базу знаний.

Правило 1.

«Если вариант h_j обеспечивает прирост товарной продукции и обеспе­чивает увеличение прибыли, то вариант h_j будет принят».

Правило 2.

«Если вариант h_j обеспечивает снижение себестоимости товарной про­дукции и прирост производительности труда, то вариант h_j будет принят».

Правило 3.

«Если вариант h_j требует не более заданного уровня прироста численно­сти работающих и обеспечивает увеличение среднегодовой производствен­ной мощности, то вариант h_j будет принят».

Правило 4.

«Если вариант h_j требует не более заданного объема капитальных вло­жений или не более заданного объема капитальных вложений на строитель­но-монтажные работы, то вариант h_j будет принят».

Правило 5.

«Если вариант h_j укладывается в лимит капитальных вложений и обеспечивает заданный уровень фондоотдач, то вариант h_j будет принят».

Правило 6.

«Если вариант h_j предусматривает заданные сроки завершения или если

затраты на мероприятие по защите окружающей среды находятся на задан­ном уровне, то вариант h_j будет принят».

Таблица 9.5 соответствует простым гипотезам, таблица 9.6 — эмпириче­ским гипотезам.

В процессе работы ЛПР инженер по знаниям может задать вопросы типа: «Какой уровень фондоотдачи вы считаете достаточным и необходимым для того, чтобы проект был принят». На основании обработки мнений ряда экспертов могут быть построены оценки p(h/x). Исходя из вида функциональ­ной зависимости p(h/x) и принимая во внимание расчетные значения эконо­мических показателей, инженер по знаниям оценил соответствующие значе­ния вероятностей, приведенные в таблице 9.5. Данные сравнения гипотез, рассчитанные непосредственно по формулам (9.37-9.42), приведены в таб­лице 9.5. Данный пример является условным для нормированных значений 0<х<1.

Таблица 9.5

Коэффициенты уверенности простых гипотез

В таблице 9.6 представлены коэффициенты уверенности сложных гипо­тез, рассчитанные по формулам (9.51- 9.56).

Таблица 9.6

Коэффициенты уверенности сложных гипотез

В таблице 9.6 представлены значения коэффициентов уверенности по отдельности для каждой строки. Объединение этих данных в результирующий коэффициент уверенности можно произвести, объединяя по шагам знания, содержащимся в первой и последующих строках, используя формулы (9.49) и (9.50). Данные такого пошагового накопления коэффициента уверенности представлены в таблице 9.7.

Таблица 9.7

: Коэффициенты уверенности, накапливаемые по мере интеграции данных в строках 1-6 таблицы 9.6, рассчитанные по формулам (9.49-9.50)

Таким образом, данные таблицы 9.7 показывают, что фактор уверенности в пользу первой гипотезы 0,88 значительно превосходит фактор уверенности в пользу второй гипотезы, и гипотеза h₁ (т.е. вариант реконструкции) будет принята.

Рассмотренные примеры показывают рациональные пути интеграции процесса поиска данных с процессом подготовки решений. При этом про­блемным остается вопрос о том, какими средствами можно было бы автома­тически строить отношения базы знаний, опираясь на сверхбольшие базы документальных и фактографических данных.