Глава 9. Стратегия вывода с использованием байесовского подхода

9.1. Обработка свидетельств в условий неуверенности и нечеткости

В области экономики типичными являются ситуации, когда решения приходится принимать на основе неточных данных. Элементы данных, с которыми имеют дело эксперты в процессе принятия решений, могут быть неполными, неточными, неотчетливыми, взаимно несовместимыми и изме­няющимися во времени.

Предположим, что для любого объектанекоторого множества X и любого свойства из некоторого множества Y можно оценить количественное или качественное свойства значения Благодаря этому возникает возможность определить объект, точнее подмножество объектов через опе­ратор (квантор) , т.е. тот объект для которого выполняется свойство Y(x). Фактически процесс оценки значения свойства можно рас­сматривать как отображение (морфизм) (рис. 9.1).

Рис. 9.1. Оценка значений свойств объекта

В общем случае высказывание р(х) об индивидах (объектах) определяет некоторое множество х:р(х), а именно множество всех индивидов, для кото­рых это высказывание истинно. Истинное значение предложения зависит от уровня знания в то время, когда оно рассматривается. Таким образом, для каждого уровня знания q может быть определена совокупность p_q(x): извест­но, что на уровне знания q верно р(х). Эту совокупность p_q будем называть объемом р на уровне q. Таким образом, для данной шкалы уровней знания сопоставление уровню q множества p_q определяет отображение q set, где set— некоторое множество, более того, если истинность сохраняется во времени, то из того, что х₀ p_q и q r вытекает, что х_о р_г. Поэтому если q  r,тo p_q  p_r.

Неопределенность и неточность данных могут рассматриваться как две противоположные точки зрения на одну и ту же реальность — непол­ноту информации. В этих условиях мы определим информационную еди­ницу четверкой (объект, свойство, значение, уверенность). Неточность относится к содержанию информации, а неопределенность — к ее истин­ности, понимаемой в смысле соответствия действительности («уверенно­сти»). Степень неопределенности информации отражают с помощью квалификаторов (модальностей) типа «вероятно», «возможно», «необходимо», «правдоподобно» и др. Правдоподобность и доверие имеют чисто эписте­мологическую интерпретацию и связаны с возможностью и необходимо­стью. Каждое из этих понятий соответствует некоторому способу вывода из заданной суммы знаний: заслуживает доверия все, что непосредственно дедуктивно выводится из базы знаний, а правдоподобно все, что не проти­воречит ей.

Будем называть информационное данное точным, если подмножество его значений является синглетоном. Мы будем называть предложение неопределенным, если его справедливость или ложность не может быть определенно установлена. Предложение, содержание которого суть высказывание о значе­нии некоторой переменной, является неточным, если это значение недоста­точно точно определено по отношению к данной шкале. Для заданного мно­жества сведений противоречие между неточностью и неопределенностью вы­ражается в том, что с повышением точности содержания возрастает его неоп­ределенность, и наоборот, неопределенный характер точной информации при­водит в общем случае к некоторой неточности окончательных заключений, выводимых из этой информации.

Одним из существенных достоинств ИИС является создание методов, позволяющих быть точными в отношении неточных данных. Нечеткая логика создана Л. Заде, который распространил булеву логику на действительные числа. В нечеткой логике используются все значения между 0 и 1, чтобы указать частичную истину. Так, запись: Р(конкурентноспособный (х)) = 0,75 говорит о том, что предложение «х— конкурентноспособный» в неко­тором смысле на три четверти истинно. Точно так же оно на одну четверть ложно.

В основе нечеткой логики лежит определение нечеткого множества, т.е. «класса» с континуумом степеней принадлежности. Пусть X— пространство точек (объектов) с порождающим элементом х, обозначаемым х. Таким образом, X = {х}. Нечеткое множество (класс) А в X характеризуется функцией принадлежности, которая связывает с каждой точкой в X реальное число в ин­тервале [0,1] со значением _А(х) в точке х, представляющее степень принад­лежности х к А. Когда А есть множество в обычном смысле слова, его функция принадлежности может принимать только два значения 0 и 1, причем  (х) = 1 или 0 согласно тому, принадлежит ли х А или нет. Таким образом, в этом случае  (x) сводится к характеристической функции множества.

Необходимо отметить, что хотя функция принадлежности нечеткого множества имеет некоторое сходство с функцией плотности вероятности, между ними имеются существенные различия. Множество, состоящее из точек х, для которых  имеет ненулевое значение, называется базой А.

Среди обычных множеств, описывающих нечеткое множество А часто используются следующиедва множества:

— база (носитель) нечеткого множества. Нечеткое множество является нормальным, если его функция принад­лежности достигает значения 1 по крайней мере в одной точке области. Оно называется регулярным, если и только если функция принадлежности имеет только один пик, т.е. для

Над нечеткими множествами возможно выполнение теоретико-множественных операций. Объединение нечетких множеств определяемы следующим образом:

Множеством α-уровня или α-срезом нечеткого множества А называется множество

где I — интервал [0,1]. Любое нечеткое множество может быть представлено объединением своих а-уровневых множеств по всем αL. Иными словами:

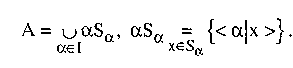
Степенью включения множества А в В называется величина

где операция импликации —> определяется согласно логике Лукасевича:

или согласно Заде:

Степень равенства нечетких множеств

Степенью ε множества А называется нечеткое множество

При ε = 2 получаем операцию концентрации, подчеркивания централь­ных элементов. Это осуществляется уменьшением периферийных значений

При ε = 0,5 получается операция размывания, растяжения центрального элемента:

Декартовым, произведением нечетких множеств A_i, i = l,n называется множество

Нечеткие отношения. Определим в общем случае n-арное нечеткое от­ношение как нечеткое подмножество в произведении пространств Х...Х .

Нечетким отношением R на множестве X называется нечеткое подмно­жество декартова произведения Х...Х , характеризующееся функцией при­надлежности в случае бинарного отношения Значение этой функции понимается как субъективная мера или степень вы­полнения отношения xRy.

Если множество X, на котором задано нечеткое отношение R, конечно, то

функция принадлежности _R этого отношения представляет собой квадратную матрицу. Если элемент r_ij этой матрицы равен α, то это означает, что степень выполнения отношения x_irx_j равна α.

Операции над нечеткими отношениями.

Пусть на множестве X заданы два нечетких отношения А и В, т.е. в декар­товом произведении X X заданы два нечетких подмножества А и В. Не­четкие множества называются соответственно объединением и пересечением нечетких отношений А и В на множестве X с функциями принадлежности:

Говорят, что нечеткое отношение В включает в себя нечеткое отношение А, если для нечетких множеств А и В выполнено условие AВ. Для функ­ций принадлежности этих множеств неравенство выполняется при любых

Если R — нечеткое отношение на множестве X, то нечеткое отношение R, характеризующееся функцией принадлежности

называется дополнением в X отношения R.

Обратное к R нечеткое отношение R ^-1 на множестве X определяется следующим образом:

Максиминное произведение А В нечетких отношенийА и В на множе­стве Охарактеризуется функцией принадлежности вида

Минимаксное произведение нечетких отношений А и В на Х определяет­ся функцией принадлежности вида

Максмультишгакативное произведение нечетких отношений А и В определяется функцией принадлежности вида

Пример расчета различного вида произведений нечетких отношений

Проекции нечетких отношений. Пусть R— нечеткое отношение на множестве X с функцией принадлежности _R(x,y). Для произвольного у  X нечеткое множество R(y) представляет собой нечеткое множество эле­ментов х множества X, связанных с выбранным у отношением R. Функция принадлежности этого множества имеет вид, где у — фиксированный элемент множества X.

Например, для нечеткого отношения R=(«близко к») заданного на число­вой оси, множество R(y) можно понимать как нечеткое множество чисел, близких к выбранному числу у.

Объединение нечетких множеств R(y) по всем уХ называется первой проекцией R⁽¹⁾ нечеткого отношения R.

Согласно определению первой проекции R⁽¹⁾ функция принадлежности и _R¹ имеет вид:

Вторая проекция R⁽²⁾ нечеткого отношения R определяется аналогичным образом:

Если R = R^(l)R⁽²⁾ — декартово произведение первой и второй проекций нечеткого отношения R, то R R . Этот факт следует из определения функ­ции принадлежности декартова произведения нечетких множеств

Пример. Пусть матрица нечеткого отношения R на множестве , имеет вид:

Тогда функции принадлежности первой и второй проекций этого отно­шения таковы:

Свойства нечетких отношений.

1. Рефлексивность.

Нечеткое отношение R на множестве X называется рефлексивным, если для любого х Х выполнено равенство

В случае конечного множества X главная диагональ матрицы рефлексив­ного нечеткого отношения R состоит целиком из единиц. Примером рефлек­сивного нечеткого отношения может служить отношение «примерно равны» в множестве чисел.

2. Антирефлексивность.

Функция принадлежности антирефлексивного нечеткого отношения об­ладает свойствомпри любом хХ. Антирефлексивно, например, отношение «много больше» в множестве чисел. Дополнение рефлексивного отношения антирефлексивно.

3. Симметричность. Нечеткое отношение R на множестве X называется симметричным, если для любых х, у X выполнено равенство

Матрица симметричного нечеткого отношения, заданного в конечном множестве, симметричная. Пример симметричного нечеткого отношения — отношение «сильно различаться по величине».

4. Антисимметричность. Функция принадлежности антисимметричного нечеткого отношения обладает следующим свойством:

Это свойство можно описать следующими двумя эквивалентными спосо­бами:

Антисимметричным, например, является нечеткое отношение «много больше».

5. Транзитивность. Нечеткое отношение R на множестве X называется транзитивным, если RRR.

Всюду ниже под транзитивностью нечеткого отношения мы будем пони­мать максиминную транзитивность, т.е. считать, что при любых х,уХ функция принадлежности транзитивного нечеткого отношения R на множе­стве X удовлетворяет неравенству

6. Транзитивное замыкание R нечеткого отношения

Отображение нечетких множеств.

1. Образ нечеткого множества при обычном (четко описанном отображе­нии).

Пусть φ: X→Y— заданное отображение и пусть А— нечеткое подмножество множества X с функцией принадлежности _А(х).

Образ А при отображении φ определяется как нечеткое подмножество множества Y, представляющее собой совокупность пар вида

где _B : Y →[0,1] — функция принадлежности образа. Функцию принадлежности l_B(y)можно записать

где множество φ^-1(у)для любого фиксированного yY имеет вид

т.е. представляет собой множество всех элементов х Х, образом каждого из которых при отображении φ является элемент y.

Нечеткое отображение можно описать как отображение, при котором элементу хХ ставится в соответствие не конкретный элемент множества Y, а нечеткое подмножество множества Y.

Описывается нечеткое отображение функцией видагак,

что функция (х_о,у)(при фиксированном х = х₀ есть функция принадлеж­ности нечеткого множества в Y, представляющего собой нечеткий образ элемента х₀ при данном отображении.

Итак, пусть— заданное нечеткое отображение, и пусть

_А(х) — заданное нечеткое множество в X. Если применить принцип обобщения в форме для нахождения образа этого нечеткого множества при отображении _φ, то получим совокупность пар видапри каждом фиксированном хХ (т.е. в каждой такой паре) представляет собой нечеткое подмножество множества Y. Образ нечеткого множества _А представляет собой нечеткий подкласс класса всех нечетких подмножеств множества Y.

Определив размытые отношения, перейдем к определению понятия не­четкой реляционной базы данных.

Нечеткая реляционная база данных — это множество отношений, составленных из кортежей (строк), содержащих n элементов. Пусть t_j — j-я строка, она принимает вид— значение домена, выбранное из домена Dj. В любой обычной реляционной базе данныхДля размытой реляционной базы данных d_ij не обязательно является синглетоном, т.е.Вторая особенность нечеткой реляционной базы данных состоит в том, что для каждого домена D_j определяется отношение сходства S_j, определенное на декартовом произведении

Отношение сходства есть обобщение отношения эквивалентности такое, что если a,b,c D., то имеют место свойства

Интерпретация кортежа есть любое приписывание значения такое, что a_j,  d_ij для всех j. Для множества i кортежа tj существует q возможных интерпретаций, где α_i равно мощности декартова произведения значений доменовОтвет на запрос есть отношение, образованное из области, релевантной запросу. В обычной базе данных каждый кортеж в отношении ответа полностью со­вместим с критерием выдачи, определенным в запросе. В нечеткой базе данных каждый кортеж получает некоторое значение функции принадлеж­ности. Обычно коэффициент степени принадлежности является мерой со­ответствия (пригодности) кортежа как реакции на данный размытый за­прос.

Ответ на размытый запрос будет иметь меру принадлежности, заключен­ной между нулем и единицей. Способность специфического запроса разли­чать кортежи в отношении реакции пропорционально степени, с которой запрос экстремизирует значения функции принадлежности кортежа множе­ству релевантных записей. В данном случае термин «экстремизирует» имеет смысл приближения к концам интервала значений декартова произведения значений доменов области

лингвистическими формами, выражающими соответствие кортежа за­просу, являются такие формы, как «нет», «очень», «более или менее», «не очень» соответственно им используются лингвистические модификаторы, выражаемые, в частности, с помощью функций CON — концентрации и DIL — размывания.

Пусть— произвольный элемент. Значение функции принадлежности, где определяется как. Запрос Q(.) индуцирует значения функции принадлежности _Q(t)для строки t в выдаче r следующим образом: каждая интерпретация

определяет значение _а(а^`_j)для каждого элемента домена. Оценка модификаторов и операторов в Q на осно­ве значений функции принадлежности _a (а_j) дает _q(I) , значение функции принадлежности по отношению к запросу. Наконец,

Нечеткая переменная определяется кортежем —

наименование нечеткой переменной, X = х — область определения нечеткой переменной (базовое множество),— нечеткое подмножество множества X, описывающее ограничения на возможные значения нечеткой переменной α .

Лингвистическая переменная характеризуется набором

, в котором β — название лингвистической переменной, Т(β)— термин-множество лингвистической переменной β, т.е. множество лингвистических (вербальных) значений переменной, причем каждое из этих значений является нечеткой переменной с областью определения X: G —

синтаксическое правило (имеющее обычно форму грамматики), порождающее наименования αТ(β) вербальных значений лингвистической перемен­ной β, М — семантическое правило, которое ставит в соответствие каждой нечеткой переменной α  Т(β) нечеткое множество С(α) —смысл нечеткой переменной а.

Заметим, что Т— множество значений лингвистической переменной (терм-множество), представляет собою наименования нечетких переменных, областью определения которых является множество X. G — синтаксическая процедура (грамматика), позволяющая оперировать элементами терм-множества Т, в частности генерировать новые осмысленные термы. Множе­ство называется лингвистической переменной, образуемой процедурой G. G позволяет осуществить отображение лингвистической переменной в нечеткую переменную, т.е. приписать нечеткую семантику путем формирования соответствующего нечеткого множества.

Синтаксис G задается в виде бесконтекстной грамматики где V_N — множество нетерминальных символов, V_T —множество терминальных символов, W — начальный символ, П — множест­во продукций. Множество терминальных символов включает множество базовых значений Т, логические операции и модификаторов И, ИЛИ, ОЧЕНЬ, НЕ, СЛЕГКА и др. Семантическую процедуру можно задать правилами

где C₁ и С₂ нечеткие множества, соответствующие значениям а₁ и а₂ рассматриваемой лингвистической переменной.

Лингвистические переменные, у которых процедура образования новых значений G зависит от множества базовых значений Т, назовем синтаксиче­ски зависимыми лингвистическими переменными.

Нечеткими высказываниями назовем высказывания следующего вида:

• высказывание <β есть α>, где β— наименование лингвистической переменной, отражающей некоторый объект или параметр реальной действительности, относительно которой производится утверждение α, являющееся ее нечеткой оценкой (нечеткой переменной), например: «Ве­личина задолженности равна 14 млн.руб.», здесь α =14 является оценкой лингвистической переменной β <задолженность>:

• < β есть α >;

• < β есть mα>, где m — модификатор «очень», «более или менее», «не­ значительный»;

• < β есть Qα >;

• < Qβ есть mα >;

• <mβ есть Qα >, где Q — квантификатор («большинство», «несколько», «много», «немного»);

• высказывания, образуются из вышеперечисленных с использованием союзов И, ИЛИ, ЕСЛИ ... ТО, ИНАЧЕ.

Пусть— множество признаков, значениями которых описывается состояние объекта управления. Каждый признак описывается соответствующей лингвистической перемен­ной у_i(набор лингвистических значений признака, m_i — число значений признака), D — базовое множество признака уi Для описания термов соответствующих значениям признака y_i, используют­ся нечеткие переменные, т.е. значение Тⁱ_j описывается нечетким множеством C_Jⁱ в базовом множестве D_i:

Нечеткой ситуацией S называется нечеткое множество второго уровня

Пример 9.1. Нечеткая ситуация.

{<<0,1 / «большая»>, <0,8 / «средняя»>, <0,4 / «малая»> / «рентабель­ность производства»>, <0,6/ «большая»>, <0,8/ «небольшая»>, <1,0/ «сред­няя»»/ «величина прибыли)>}.

Рассмотрим пример применения правил нечеткой логики к выбору цен­ных бумаг.

Предположим, что имеются ценные бумаги, возможность приобретения которых представлена в виде следующих данных в таблице 9.1:

Таблица9.1

Заметьте, что сумма возможностей не равна 1. Когда неопределенность представляется возможностью, может быть применена размытая логика. Возможность того, что ценная бумага даст высокий доход, обозначается _s(high(x)) функция ₅(х) является в данном случае функцией принадлежности, причем 0 < _s(x) < 1.

Подход с позиций размытой логики может быть применен в ИИС для представления правил вывода в условиях нечеткости. Предположим, что существует два правила с нечеткими условиями.

Пример 9.2.

Правило 1.

IF <x> хорошо экспортируется(0,6)

AND <x> принадлежит к электронной отрасли (1,0)

THEN <х> обеспечивает высокий доход.

Правило 2.

IF<x> принадлежит большому объединению (0,5)

AND <x> имеет высокую активность в проведении научных исследо­ваний (0,25).

THEN <x> обеспечивает высокий доход, где переменная <х> заменяет название фирмы.

Любые ценные бумаги, которые удовлетворяют правилам 1 и 2 могут быть отнесены к системам с высоким доходом с данной степенью уверенно­сти, следовательно интеграция двух условий должна производиться связкой ИЛИ (OR).

Так как каждое правило содержит конъюнкцию свидетельств, то общая оценка возможности события, определяемого правилом, определяется сле­дующим образом:

Правило 1: Min(l,0; 0,6)=0,6

Правило 2: Min(0,5; 0,25)=0,25

Далее два правила интегрируются посредством связки OR

Правило 1 или 2

Мах(0,6; 0,25)=0,6.

Согласно правилам нечеткого множества, мы можем заключить, что ценная бумага <х>, которая удовлетворяет либо правилу 1, либо правилу 2 обеспечивает значение возможности получения высокого дохода, рав­ное 0,6.

При использовании правил нечеткой логики нужно следить за тем, чтобы не было потеряно много информации в процессе интеграции свидетельств. В примере 9.2 информация

<x> хорошо экспортируется (0,6)

<x> принадлежит большому объединению (0,5)

вовсе не использовалась. Чтобы компенсировать это дефект, может быть использована следующая формула редактирования, предложенная Шортли-фом:

Шортлиф первым назвал величину, определяемую формулой (9.1), мерой уверенности. Но так как его определение меры уверенности перекликается с определением величины MB, которое приводится в последующих разделах, более правильно определить формулу (9.1) как компенсаторное правило размытой логики. В соответствии с этим правилом, получим:

До сих пор мы предполагали, что правила сами по себе не являются неопределенными, они являются твердо установленными фактами. Если имеются сомнения относительно самих правил вывода, чтобы ослабить возможность заключения благодаря такой неопределенности, введем меру доверия правилу CR . В этом случае: