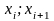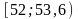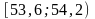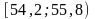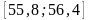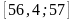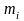Критерій згоди Колмогорова

Критерій згоди χ² дозволяє перевірити гіпотези про узгодження даних вибір­ки з конкретним теоретичним законом розподілу для будь-якої випадкової величи­ни, як неперервної, так і дискретної.

Критерій λ Колмогорова застосовується для перевірки гіпотези про закон роз­поділу тільки неперервних випадкових величин. Його відмінність від критерію χ² Пірсона полягає в тому, що порівнюються не емпіричні і теоретичні частоти, а емпі­рична і гіпотетична функція розподілу ймовірностей, а також припускається, що те­оретичні значення параметрів дійсної функції розподілу відомі.

Перевірку нульової гіпотези за допомогою критерію згоди Колмогорова проводять по наступній схемі:

1. Знаходимо емпіричну функцію розподілу ;

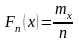2. Знаходимо значення теоретичної функції розподілу, що відповідають спосте­реженим значенням випадкової величини X;

3. Знаходять для кожного значення x_j, модуль різниці між емпіричною і тео­ретичною функцією розподілу, тобто |F_n(x) - F(x)|,

обчислюють значення вибіркової статистики Колмогорова λ=max|F_n(x) - F(x)|

4. Порівнюють спостережене значення вибіркової статистики λ з критичним значенням λ_α, знайденим за таблицею розподілу Колмогорова при заданому рівню значущості α .При цьому, якщо λ < λ_α, то немає підстав для відхилу нульової гіпотези, якщо λ ≥ λ_α приймається конкуруюча гіпотеза Н₁.

Домашнє завдання

Використовуючи критерій Пірсона при рівні значущості 0,05 перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х із заданим емпіричним розподілом

	4	16	35	17	3

Лекція 13 Поняття про кореляційну залежність. Лінійна кореляція.

Метод найменших квадратів

Випадкові величини X i Y називають стохастично залежними, якщо зміна однієї з них призводить до зміни розподілу другої. Зокрема, може змінюватися той чи інший параметр розподілу. Якщо зі зміною однієї випадкової величини зміщається центр розподілу другої, тобто її середнє значення, то стохастичний зв’язок між величинами зветься кореляційним.

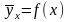(13.1)

Рівняння виду (13.1) визначає кореляційну залежність Y від X, його називають рівнянням регресії Y по X. Ламана, побудована за емпіричними даними, являється емпіричною лінією регресії. Теоретичною лінією регресії служить графік функції f(x).

Аналогічно рівняння регресії X по Y задається рівністю

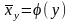(13.2)

Якщо обидві функції f(x) i φ(y) лінійні, то кореляцію між X i Y називають лінійною. В протилежному випадку говорять про нелінійну кореляцію.

В теорії кореляції розглядають такі дві основні задачі:

1) встановити вигляд функції регресії f(x) i φ(y);

2) оцінити "тісноту" кореляційного зв’язку випадкових величин.

Якщо які-небудь теоретичні передумови відсутні, то вибір функцій (13.1) і (13.2) можна здійснити у такий спосіб: припустимо, наприклад, що f(x) – лінійна функція, що задовольняє рівнянню

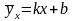, (13.3)

де параметри k і b треба знайти за вибірковими даними. Як правило, ці параметри шукають методом найменших квадратів. У найпростішому випадку залежність (13.3) дає нев’язку (відхил)

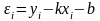, (13.4)

яка у загальному випадку відмінна від нуля.

В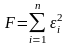 еличина

(13.5)

характеризує сумарну похибку наближення даної сукупності точок (x_i, y_i) за допомогою прямої

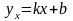, (13.6)

Зі змінною k і b змінюється і величина F, обчислена за формулою (13.5), тобто F залежить від k і b:

F=F(k, b). (13.7)

Підберемо параметри k і b так, щоб сума квадратів відхилень точок (х_і, у_і) від прямої (13.6) була найменшою, тобто, щоб мінімальне значення приймала функція

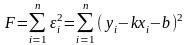. (13.8)

У цьому і полягає суть методу найменших квадратів.

Для знаходження мінімуму функції (13.8) знайдемо частинні похідні функції F за змінними k і b, а потім прирівняємо їх до нуля.

Маємо

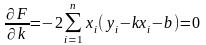
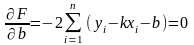
або

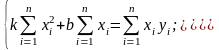(13.9)

Ця система зветься нормальною системою рівнянь, яку можна розв’язати відносно k і b.