3.2Дисперсия св. Понятие среднего квадратического отклонения (ско).

3.2.1Определение дисперсии

Степень группирования (или степень рассеивания) СВ относительно центра рассеивания (МО) характеризуется дисперсией. Рассеивание СВ X связано с отклонением (x - a_X ), где a_X – центр рассеивания (a_X = M_X).

Отклонение СВ X (x-a_X ) называют также центрированной СВ X*.

M(X*) = 0

Дисперсией называют МО квадрата отклонения СВ X от своего МО.

Дискретная СВ:	или
Непрерывная СВ:	или

Средним квадратическим отклонением СВ называют квадратный корень из дисперсии.

Случайная величина вида называется нормированной СВ.

3.2.2Свойства дисперсии

Свойство 1.

Свойство 2.

Свойство 3. , если X и Y независимые СВ

Следствие: Дисперсия суммы случайных величин, независимых в совокупности равна сумме дисперсий этих СВ.

Свойство 4.

Следствие:

Пример 1. Рассчитать дисперсию для СВ распределенной по закону Бернулли.

n=1
n

Пример 2.

Найти дисперсию СВ, плотность распределения вероятности которой задана следующей функцией:

3.2.3Другие характеристики рассеивания

Среднее абсолютное отклонение СВ:

Квантиль -такое значение , для которого

В частности , и квантили делят площадь под кривой распределения на 4 равные части.

3.3Начальные и центральные моменты.

Начальным момент k-го порядка

Центральный момент k-го порядка

Математическое ожидание СВ – начальный момент 1-го порядка.

Дисперсия СВ – центральный момент 2-го порядка.

4Типовые распределения вероятностей

4.1Типовые распределения дискретных СВ

4.1.1Распределение выборочного значения признака

Пусть имеется совокупность элементов (предметов, явлений), различающихся величиной некоторого общего признака (группа студентов-признак «рост»).

x₁, x₂,.., x_k – различные значения признака у элементов совокупности.

M₁, M₂, …, M_k- число элементов с заданным признаком, причем .

Выбирается 1 элемент. Какова величина признака у выбранного элемента или выбранного значения признака? Очевидно, что X – дискретная СВ с возможными значениями x_i. Имеем схему распределения вероятностей –

4.1.2Геометрическое распределение

Проводится серия опытов. В каждом опыте событие A появляется с вероятностью p и не появляется с вероятноятностью q=1-p. Серия заканчивается при первом же появлении события A. Тогда СВ X – число испытани, которое надо провести до первого появления события A, а вероятность того что x=m есть:

m = 1,2,3,…

p = p,qp,qqp,… - геометрическая прогрессия со знаменателем q

Ряд P_m – сходится, а его сумма равна 1.

4.1.3Гипергеометрическое распределение

В партии N изделий, среди них M стандартных. Случайно отбирается n изделий (без возврата – формула Бернулли не применима). X –СВ, число m стандартных изделий из n отобранных.

X=m, => 0,1,2,…, min{M,n}

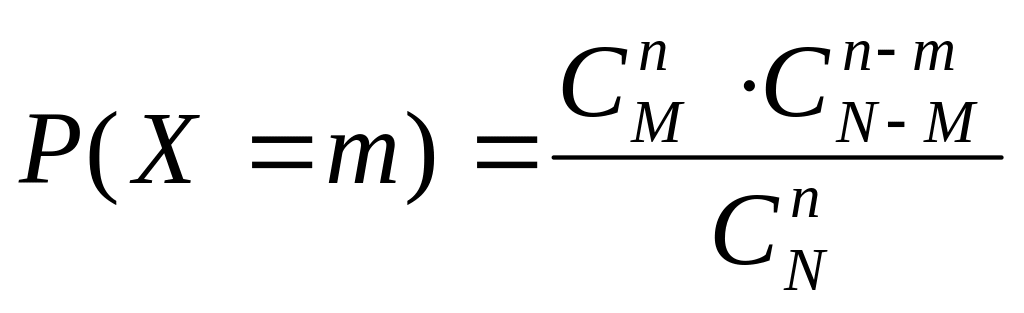
4.1.4Биномиальный закон распределения

Биномиальным называют закон распределения дискретной СВ X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p (а не появления соответственно q). Распределение вероятностей определяется формулой Бернулли.

m – число раз появления события

4.1.5Отрицательное биномиальное распределение

Описывает распределение СВX – числа испытаний в схеме Бернулли до k-го интересующего события (включая последнее испытание).

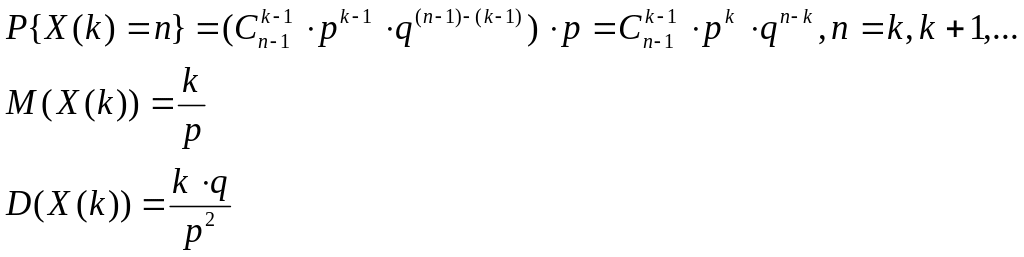
4.1.6Распределение Пуассона.

Введем распределение Пуассона через биномиальное распределение. Заданы n, p, q = 1-p. При этом p <= 0.1 (вероятность появления события очень мала), а n достаточно велико. Введем допущение: , то есть среднее число появления события в различных сериях испытаний (различные значения n) остается неизменным.

{так как , то } =

т.к. n – велико, существуют определенные трудности вычисления P_n,m. Перейдем к приближенному определению как предельному значению, к которому стремиться данное соотношение.

таким образом получаем:

Распределение Пуассона имеет смысл для массовых, редких событий !!

Для этого распределения характерно:

На практике распределение Пуассона используется:

1. Для приближенного вычисления вероятностей Pn,m биномиального закона распределения при достаточно больших n и p <= 0.1.

2. для характеристики распределения простейшего потока событий во времени

Поток событий – последовательность событий, наступающих в случайные моменты времени.

Простейший пуассоновский поток событий – поток событий, обладающий свойствами стационарности, отсутствия последействия и ординарности.

Стационарность – вероятность появления K событий за промежуток времени длительностью t , есть функция, зависящая только от K и длительности t, но не зависит от начала его отсчета. Иначе,: интенсивность потока событий во времени есть величина постоянная ( ).

Интенсивность потока – среднее число событий появляющихся в единицу t.

Отсутствие последействия – вероятность появления K событий на любом промежутке t не зависит от того сколько раз оно появлялось в предшествующие моменты. То есть предыстория процесса не оказывает влияния на наблюдаемый процесс, или имеет место взаимная независимость появлений того или иного числа событий в непересекающихся промежутках времени.

Ординарность – появление 2-х и более событий за бесконечно малый промежуток t практически невозможно. То есть за бесконечно малый промежуток времени появляется не более одного события.

, где