Существование оптимальных стратегий. Теорема фон Неймана-Нэша
Существование оптимальных стратегий смешанного расширения игры доказывается следующей теоремой.
Теорема 2. (основная теорема матричных игр, теорема фон Неймана-Нэша). Всякая матричная игра имеет ситуацию равновесия в смешанных стратегиях.
Доказательство
1.
Пусть
– игра со строго положительной матрицей
,
где
.
Докажем справедливость теоремы для
игры с такой матрицей A.
Рассмотрим задачу линейного программирования следующего вида:
,
В векторно-матричной форме задача преобразуется к следующему виду:
(6)
где
.
Двойственная к (6) задача имеет следующий вид:
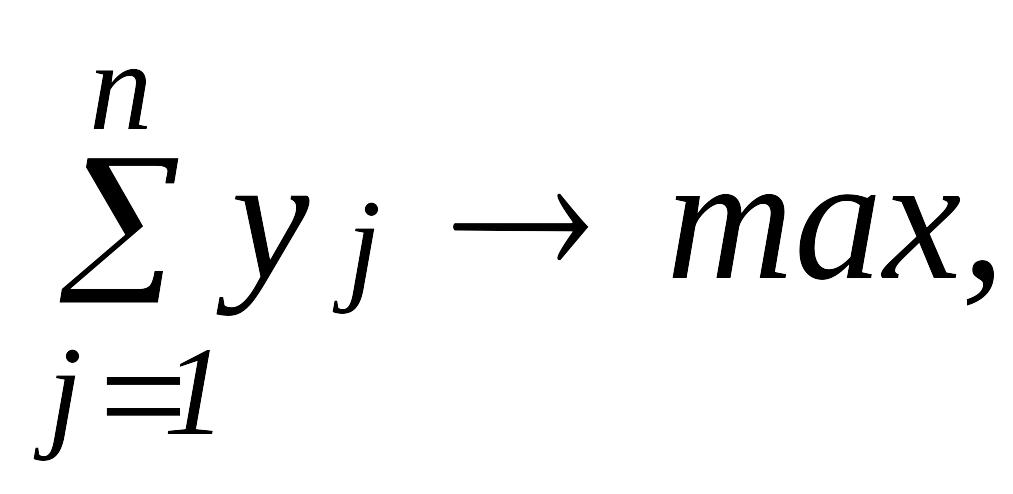
которая имеет следующую векторно-матричную форму:
(6д)
где
.
Так
как элементы матрицы A
строго положительны, то существует
вектор
,
для которого
,
то есть задача (6) имеет допустимую точку.
С
другой стороны, точка y=0
является допустимым решением (6д). Тогда
по теореме двойственности существуют
и
– оптимальные решения задач (6) и (6д)
соответственно и значения целевых
функций в оптимальных точках совпадают,
то есть
.
(7)
Рассмотрим
векторы:
,
.
Покажем,
что
,
– оптимальные смешанные стратегии в
и цена игры
.
Первоначально докажем, что , – смешанные стратегии.
Из
соотношений (7):
,
то есть
.
Из допустимости векторов
и
в задачах (6) и (6д) следует, что
,
,
то есть пара
– ситуация в смешанных стратегиях.
Докажем, что , – оптимальные смешанные стратегии.
Вычислим выигрыш первого игрока P1 в ситуации :
.
Причем,
с одной стороны,
,
а с другой –
.
Тогда
,
а
.
Пусть x, y – произвольные смешанные стратегии Р1 и Р2. Тогда выполняются неравенства:
;
.
Таким
образом,
,
,
,
то есть
– ситуация равновесия, а
– цена игры
со строго положительной матрицей A.
2. По лемме о масштабе теорема верна для игры с произвольной матрицей A, т. к. всегда существует матрица , где , такая, что элементы матрицы положительны. Теорема доказана.
Упражнения к § 2.3–2.5.
№1. Найти, опираясь на определение ситуации равновесия, ситуацию равновесия в игре со следующей матрицей:
1)
;
2)
.
№ 2.
Проверить, что
и пара
,
где
и
,
соответственно цена и ситуация равновесия
в игре с матрицей
.
№ 3. Методом сведения игры к системе неравенств найти оптимальные стратегии и цену игры, задаваемой матрицей:
.
№4.
Дана игра с квадратной матрицей
,
где
.
С помощью свойства
2 оптимальных смешанных стратегий
показать, что оптимальные стратегии
игроков равны и вычисляются по формулам:
,
а цена игры
.
№5.
Матрица порядка
называется латинским квадратом, если
каждая строка и каждый столбец ее
содержит все целые числа от 1 до m.
(Например, матрица
–
латинский квадрат). Показать, что
.
№6. Решить графически игру со следующими матрицами:
1)
;
2)
;
3)
;
4)
.
№ 7. Найти оптимальные стратегии и цену игры сведением игры к задаче линейного программирования, если матрица имеет вид:
1)
;
2)
,
3)
.
№ 8.
Игра
с квадратной матрицей A
называется симметричной, если матрица
A
является кососимметрической, т. если
,
.
Доказать, что: 1) цена симметричной игры
;
2)
множества оптимальных стратегий игроков
совпадают, то есть если
является ситуацией равновесия, то
также является ситуацией равновесия.