3.2. Принципы оптимальности в бескоалиционных играх

В §2 показано, что для антагонистических игр принципы минимакса, максимина и равновесия совпадают (если они реализуемы, то есть существует равновесие, а минимакс и максимин достигаются). В таком случае они определяют единое понятие оптимальности и решения игры. В теории неантагонистических игр нет единого подхода к выработке принципов оптимальности. Имеется целый класс таких принципов, каждый из которых основывается на дополнительных предположениях о поведении игроков и структуре игры. Рассмотрим основные подходы, используемые для принятия решений в неантагонистических бескоалиционных играх: равновесие в доминирующих стратегиях, равновесие по Нэшу, равновесие по Парето, равновесие по Штакельбергу.

1. Равновесие в доминирующих стратегиях

Аналогично антагонистическим играм введем понятие доминирующих стратегий игроков для бескоалиционных игр N лиц.

Определение 13. Стратегия игрока в игре доминирует стратегию , если для любого вектора выполнено:

и существует такой, что

.

Итак, стратегия игрока доминирует , если независимо от поведения остальных участников (игроков множества ) применение для него не дает большего выигрыша, чем , а для некоторого выбора остальных игроков ему выгоднее выбирать , чем .

Определение 14. Стратегия игрока называется доминирующей, если она доминирует любую стратегию .

Определение 15. Ситуация называется ситуацией равновесия в доминирующих стратегиях, если стратегия является доминирующей стратегией игрока .

Замечание 6. Если игрок выбирает доминирующую стратегию, то он руководствуется следующим принципом: я выбираю лучшую стратегию независимо от того, что выбрали другие.

Примеры

Пример 1. Рассмотрим биматричную игру, в которой каждый игрок имеет по две чистые стратегии, , , а матрицы выигрышей имеют вид:

, .

Проверить, есть ли в данной игре равновесие в доминирующих стратегиях.

Решение

Для игрока Р1 выполнено: , . Следовательно, доминирует .

Аналогично для Р2 выполнено: , . Тогда доминирует .

Так как для каждого игрока найдены доминирующие стратегии, то ситуация – равновесие в доминирующих стратегиях.

Пример 2. Рассмотрим игру «Семейный спор», матрица выигрышей которой имеет вид:

.

Проверить, имеет ли данная игра ситуацию равновесия в доминирующих стратегиях.

Решение

Матрица A первого игрока имеет вид: 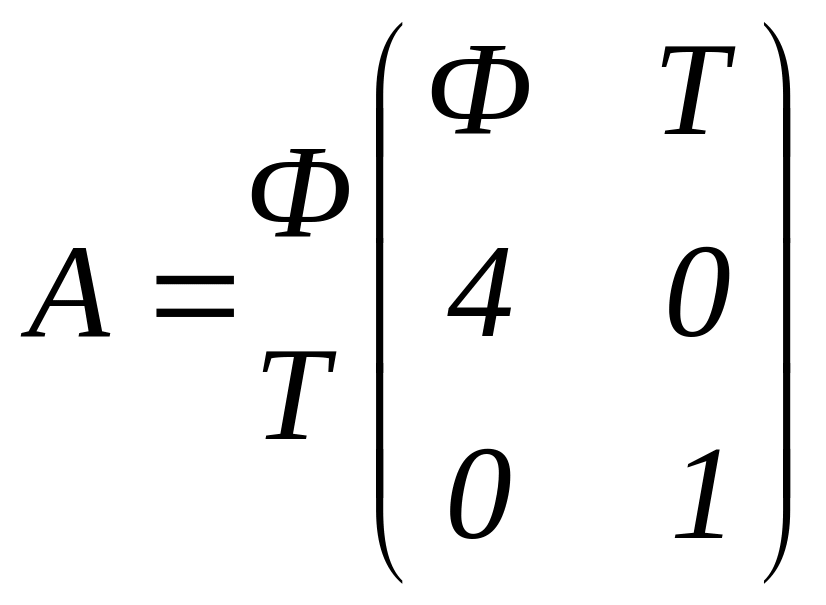. Для элементов строк матрицы выполнены следующие неравенства:

, но . Следовательно, у первого игрока нет доминирующей стратегии, и в самой игре нет ситуации равновесия в доминирующих стратегиях.

2. Равновесие по Нэшу

Пусть – произвольная ситуация в игре , – некоторая стратегия игрока . Рассмотрим вектор , получаемый из заменой стратегии игрока на стратегию .

Определение 16. Ситуация называется ситуацией равновесия по Нэшу, если для всех игроков , имеют место неравенства:

, . (10)

Таким образом, ни один из игроков не заинтересован в отклонении от стратегии , входящей в ситуацию равновесия по Нэшу (согласно (10), его выигрыш при использовании стратегии вместо разве лишь уменьшится при условии, что остальные игроки придерживаются стратегий, образующих ситуацию равновесия ). Таким образом, если игроки договорились предварительно об использовании стратегий, входящих в ситуацию равновесия , то индивидуальное отклонение от договора невыгодно отклонившемуся игроку.

Замечание 7. Если игрок выбирает стратегию , то он руководствуется следующим принципом: я выбираю лучшую стратегию при учете действий остальных участников.

Определение 17. Стратегия называется равновесной, если она входит в хотя бы одну ситуацию равновесия по Нэшу.

Для бескоалиционной игры двух лиц ситуация является ситуацией равновесия, если неравенства

, выполняются для всех , .

В частности, для биматричной игры пара является ситуация равновесия по Нэшу, если неравенства: , выполнены для всех , , то есть элемент является максимумом в столбце , а – максимумом в строке .

Замечание 8. Рассмотрим антагонистическую игру двух лиц. Обозначим . Тогда является ситуацией равновесия по Нэшу, если

, (для первого игрока),

, (для второго игрока).

Следовательно, , , . Это означает, что является седловой точкой функции выигрыша первого игрока, то есть равновесие в антагонистической игре является равновесием по Нэшу.

Примеры

Пример 1. В игре «семейный спор» с матрицей найти ситуации равновесия по Нэшу.

Решение

Рассмотрим матрицу 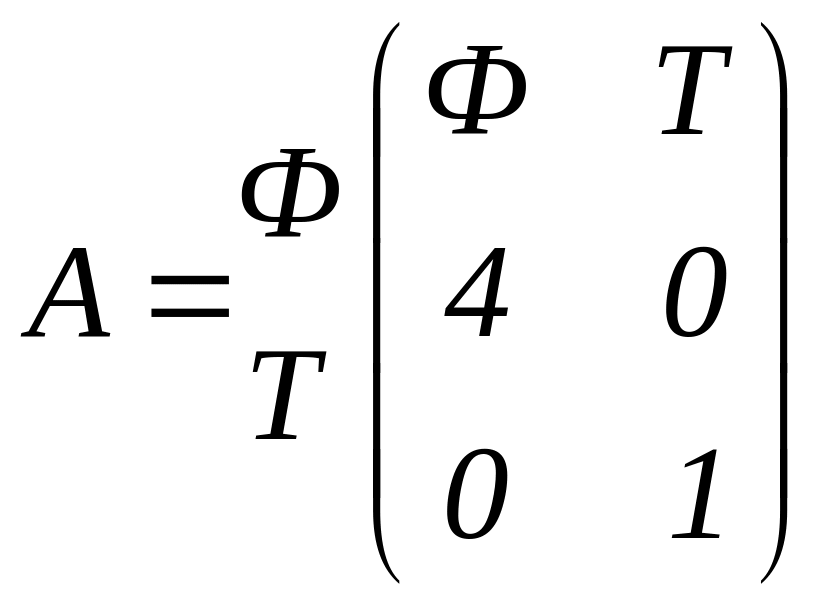. Элемент является максимальным в первом столбце матрицы, а – максимальным во втором столбце. Аналогично, для матрицы элемент является максимальным в первой строке, а – максимальным во второй строке. Следовательно, ситуации и являются ситуациями равновесия по Нэшу.

Пример 2. В игре «дилемма заключенного» с матрицей найти ситуации равновесия по Нэшу.

Решение

В матрице A первого игрока максимальным в первом столбце является элемент , а во втором столбце – . Для матрицы B максимальным элементом в первой строке является элемент , а во второй строке – . Таким образом, элемент с координатами = является максимумом во 2 столбце матрицы A и максимумом во второй строке матрицы B. Это означает, что полученная точка и является ситуацией равновесия по Нэшу с равновесным вектором выигрышей .