3. Смешанное расширение бескоалиционной игры

Рассмотрим бескоалиционную игру , где – конечное множество игроков. Пусть множество стратегий каждого игрока конечно и включает стратегий: .

В предыдущем пункте было показано, что в общем случае ситуация равновесия по Нэшу в обычных чистых стратегиях существует не всегда. Поэтому, по аналогии с антагонистическими играми, введем понятие равновесия по Нэшу в классе смешанных стратегий.

Обозначим через – вероятность выбора i-ым игроком j-ой чистой стратегии, 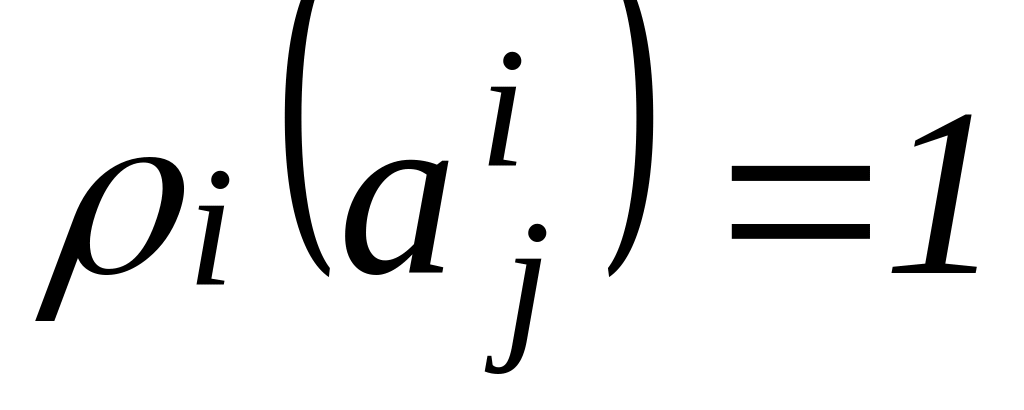, . Тогда вектор – смешанная стратегия i-го игрока, представляющая собой некоторое вероятностное распределение на множестве стратегий , которые в дальнейшем будем называть чистыми. Вектор называется ситуацией в смешанных стратегиях. Пусть – множество смешанных стратегий i-го игрока.

Рассмотрим ситуацию в чистых стратегиях . Вероятность появления этой ситуации вычисляется по следующей формуле:

. (12)

Формула (12) определяет вероятностное распределение на множестве всех ситуаций , определяемое смешанными стратегиями .

В качестве значений функции выигрыша i-го игрока в ситуации принимается математическое ожидание выигрыша:

, . (13)

Определение 22. Игра , в которой - множество игроков, – множество смешанных стратегий i-го игрока , а функция выигрыша определяется равенством (13), называется смешанным расширением игры .

Для биматричной игры множества смешанных стратегий Р1 и Р2 можно определить следующим образом:

; .

Математические ожидания выигрышей Р1 и Р2 определяются как

; , .

Определение 23. Ситуация называется ситуацией равновесия по Нэшу в смешанных стратегиях в игре , если для любого игрока и для любой его смешанной стратегии имеет место неравенство:

, . (14)

Примеры

Пример 6. Показать, что в игре «семейный спор» с матрицей ситуация , где , не является ситуацией равновесия по Нэшу в смешанных стратегиях.

Решение

Рассмотрим ситуацию , где . Найдем математические ожидания выигрышей игроков в каждой ситуации:

;

; .

Так как , то по определению 22 ситуация не является ситуацией равновесия.

Существование ситуации равновесия в биматричной игре устанавливается следующей теоремой, доказательство которой опирается на теорему Какутани.

Теорема 9. Пусть – биматричная -игра. Тогда существуют смешанные стратегии , игроков 1 и 2 соответственно, такие, что пара является ситуацией равновесия по Нэшу.

Свойства оптимальных стратегий

Для ситуаций равновесия в смешанных стратегиях неантагонистических игр справедливы свойства, аналогичные свойствам ситуаций равновесия в антагонистических играх.

Теорема 10. Для того чтобы ситуация в смешанных стратегиях в игре являлась ситуацией равновесия, необходимо и достаточно, чтобы для любых чистых стратегий , игроков выполнялись следующие свойства:

; .

Для произвольных смешанных стратегий первого и второго игроков введем в рассмотрение множества и , которые называются спектром смешанных стратегий Р1 и Р2 соответственно.

Определение 24. Смешанная стратегия , для которой , называется вполне смешанной.

Таким образом, все координаты вполне смешанной стратегии положительны.

Аналогично вводится понятие вполне смешанной стратегии второго игрока.

Теорема 11. Пусть – биматричная -игра и – ситуация равновесия по Нэшу в смешанных стратегиях. Тогда выполняются равенства:

;

для всех , .

Теорема 12 позволяет вычислять вполне смешанные ситуации равновесия.

Теорема 12. Пусть – биматричная -игра и матрицы А и В невырожденные. Если игра имеет вполне смешанную ситуацию равновесия, то она единственна и вычисляется по формулам:

;

, (15)

где ,

, . (16)

Обратно, если для векторов , определяемых равенствами (15) – (16), справедливо , , то пара образует ситуацию равновесия в смешанных стратегиях с вектором равновесных выигрышей .

Доказательство

1. Необходимость.

Пусть – вполне смешанная ситуация равновесия, тогда по теореме 2 должны выполняться равенства:

, ;

, . (17)

Другими словами, (18)

где , – выигрыши игроков в ситуации равновесия .

Умножим первое из равенств (18) на , второе на :

, что совпадает с (15)– (16).

С другой стороны, рассмотрим . Тогда , то есть , откуда получаем равенство . Аналогично доказывается представление для .

Единственность вполне смешанной ситуации равновесия следует из единственности решения системы (18) в условиях теоремы.

2. Достаточность.

По построению векторов x и y имеем: , а так как по условию, то – ситуация в смешанных стратегиях.

По теореме 1 для того, чтобы ситуация являлась ситуацией равновесия, достаточно выполнения неравенств:

, ,

,

или , .

Проверим справедливость этих соотношений для и .

Имеем:

, что и требовалось доказать.

Примеры

Пример 7. В игре «семейный спор» с матрицей найти, используя теорему 3, ситуацию равновесия в смешанных стратегиях.

Решение

Ситуацию равновесия в игре будем искать по формулам (15), (16).

Первоначально найдем матрицы и :

, .

Тогда . Аналогично .

Поэтому , . Так как , то найденная пара – ситуация равновесия в смешанных стратегиях с равновесным вектором выигрышей .