6. Исследовать на экстремум функции двух переменных.

z = 2x³ + 6xy - y² – 4.

7. Найти условные экстремумы функции при заданных условиях связи.

а) z= 2x² + 12xy + y²; x² + 4y² = 25.

8. Для предложенных данных:

• Построить точки на координатной плоскости.

• Определить вид линейной зависимости с помощью составления и решения соответствующей системы нормальных уравнений и с помощью формул, которые определяют коэффициенты через средние значения.

• Определить вид квадратичной зависимости.

• Построить найденные линии на координатной плоскости.

хi	0,7	0,9	1,2	1,3	1,7
yi	1,7	1,1	0,8	0,1	-0,5

Вариант 9

1. Найти область определения функции z = ln(x + y).

2. Вычислить приближенно arcsin .

3. Показать, что функция z = x^y удовлетворяет уравнению .

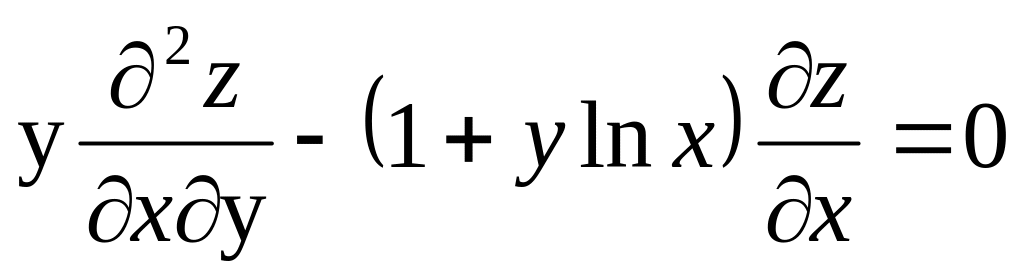4. Найти наибольшее и наименьшее значения функции z = x² + 2xy – 4x + 8y в прямоугольнике x = 0, y = 0, x = 1, y = 2.

5. Для заданной поверхности z = z(x,y) найти в точке М:

а) уравнение линии уровня функции z(x,y);

б) производную z(x,y) по направлению, заданному вектором или углом с осью Оx;

в) направление наибольшего возрастания z и производную по этому направлению.

z = - xy; M(-3; 4); =(1; -1).

6. Исследовать на экстремум функции двух переменных.

z = 2x³ – 6x² - 6xy + 3y² – 5.

7. Найти условные экстремумы функции при заданных условиях связи.

z = x² + y²; =1, a > b > 0.

8. Для предложенных данных:

• Построить точки на координатной плоскости.

• Определить вид линейной зависимости с помощью составления и решения соответствующей системы нормальных уравнений и с помощью формул, которые определяют коэффициенты через средние значения.

• Определить вид квадратичной зависимости.

• Построить найденные линии на координатной плоскости.

хi	-1,1	-0,5	0,2	0,4	0,7
yi	2,1	3,4	5,1	6,3	6,9

Вариант 10

1. Найти область определения функции z = .

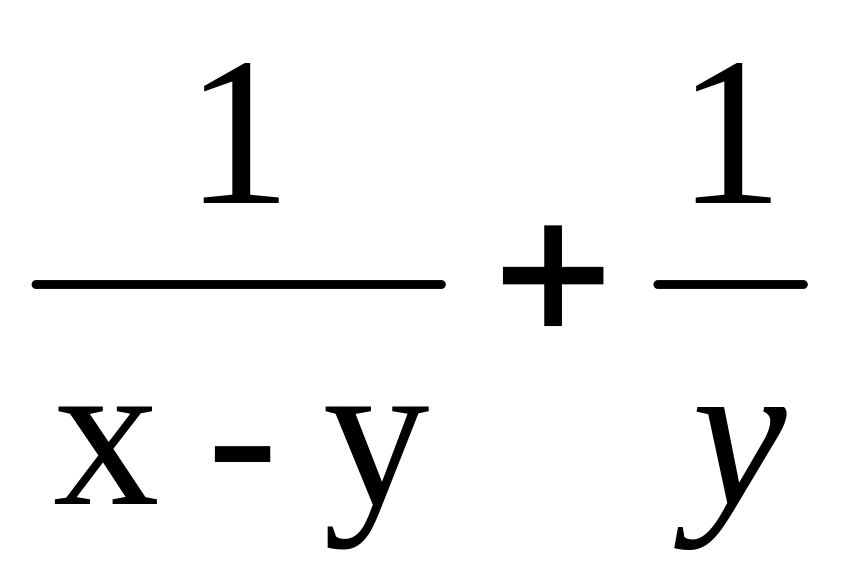2. Вычислить приближенно .

3. Показать, что функция z = x · 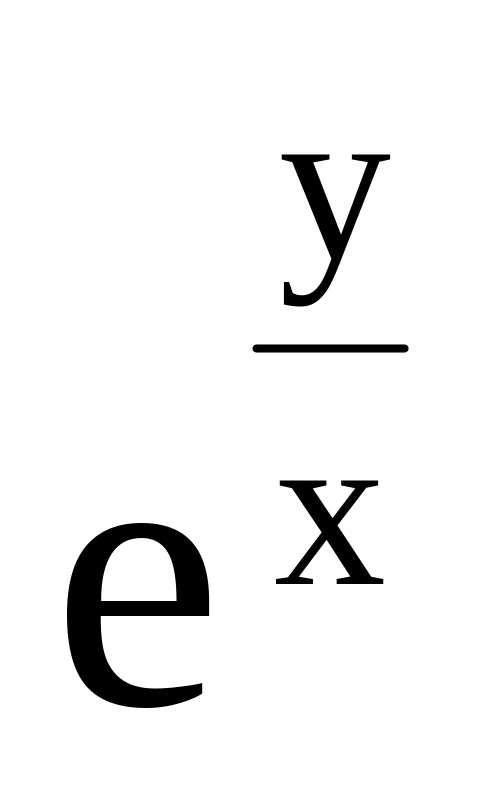удовлетворяет уравнению .

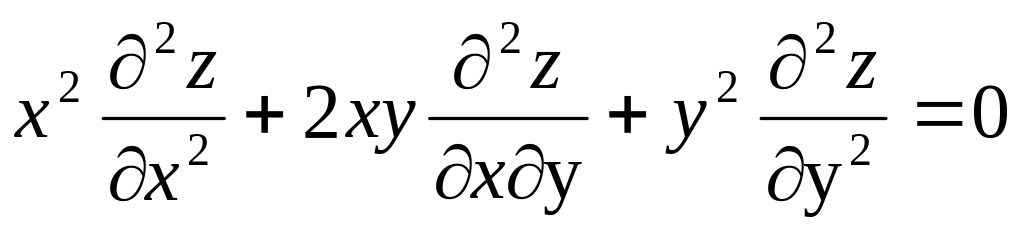4. Найти наибольшее и наименьшее значения функции z = x² – y² + 18 в круге x² + y² ≤ 9.

5. Для заданной поверхности z = z(x,y) найти в точке М:

а) уравнение линии уровня функции z(x,y);

б) производную z(x,y) по направлению, заданному вектором или углом с осью Оx;

в) направление наибольшего возрастания z и производную по этому направлению.

z = ; M(0; 1); =(1; 1).

6. Исследовать на экстремум функции двух переменных.

z = x³ + 2xy + 2y² + 2x² – 36x.

7. Найти условные экстремумы функции при заданных условиях связи.

z = , a > 0, b > 0; x² + y² = r², r > 0.

8. Для предложенных данных:

• Построить точки на координатной плоскости.

• Определить вид линейной зависимости с помощью составления и решения соответствующей системы нормальных уравнений и с помощью формул, которые определяют коэффициенты через средние значения.

• Определить вид квадратичной зависимости.

• Построить найденные линии на координатной плоскости.

хi	-1,2	-0,7	0,3	1,5	1,7
yi	5,7	5,1	0,1	0,2	-0,7