Використання функцій лгрфприбл(.) та рост(.)

На робочому аркуші виділяємо діапазон клітин A20:B20, вводимо знак “=”, aктивізуємо засіб Мастер функций. У вікнах діалогів Мастер функций вибираємо функцію ЛГРФПРИБЛ(.) та задаємо її аргументи: изв_знач_y – діапазон B4:B14, изв_знач_x – діапазон A4:A14.

П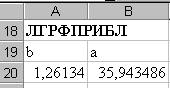 ісля натискання комбінації клавіш CTRL+SHIFT+ENTER одержуємо результат в клітинах A20, B20 (див. малюнок).

Д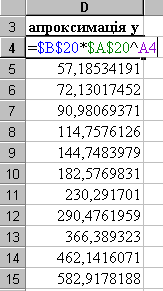 ля визначення значень апроксимації та прогнозного значення на 12-й місяць у клітину D4 вводимо формулу для обчислення значення (див. малюнок). Використовуючи автозаповнення, копіюємо формулу клітини D4 у діапазон D5:D15. Додаємо одержані значення діапазону D4:D14 на графік.

Для обчислення значень апроксимації для показникової регресії можна також скористатися функцією РОСТ(.). Виділяємо діапазон E4:E15, вводимо знак “=”, aктивізуємо засіб Мастер функций. У вікнах діалогів Мастер функций вибираємо функцію РОСТ(.) та задаємо її аргументи: изв_знач_y – діапазон B4:B14, изв_знач_x – діапазон A4:A14; нов_знач_x - діапазон A4:A15.

Використання процедури Поиск решения для обчислення параметрів регресії

Н а основі даних спостереження сформуємо цільову функцію оптимізаційної задачі для розрахунків параметрів показникової регресії методом найменших квадратів: , де - номер місяця, - відповідне значення величини прибутку; - кількість точок спостереження, - параметри регресії. Для цього на робочому аркуші у клітини A24, B24 вводимо початкові значення параметрів (числа 1 та 30), у клітини F4, G4 - формули для обчислення значень: та (див. малюнок).

Формули клітин F4, G4 копіюємо у діапазон F5:G14.

У клітину G17 вводимо формулу для обчислення суми значень діапазону G4:G14. Клітина G17 буде цільовою клітиною для засобу Поиск решения. Аналіз цільової функції оптимізаційної задачі виконується аналогічно аналізу, що був розглянутий для лінійної регресії.

Дані діапазону F4:F14 після виконання процедури Поиск решения міститимуть значення апроксимації, обчислені для оптимальних параметрів регресії. Для того щоб спостерігати за процесом виконання ітерацій процедури Поиск решения, додамо дані інтервалу F4:F14 на графік.

У вікні ініціалізації процедури Поиск решения вибираємо такі параметри:

• Установить целевую ячейку - $G$17;

• Равной - минимальному значению;

• И 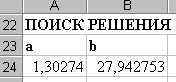зменяя ячейки - $A$24:$B$24.

Розв’язок процедури Поиск решения показано на малюнку. Прогнозне значення знаходимо, копіюючи формулу клітини F14 у клітину F15.

Використання функцій линейн(.) та тенденция(.)

Для знаходження параметрів нелінійної регресії використаємо “лінеаризовану” модель .

У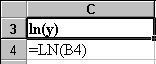 клітину C4 вводимо формулу для обчислення значення (див. малюнок), а потім копіюємо її у діапазон C5:C14.

Виділяємо діапазон клітин A29:B29, вводимо знак “=”, aктивізуємо засіб Мастер функций. У вікнах діалогів Мастер функций вибираємо функцію ЛИНЕЙН(.) та задаємо її аргументи: изв_знач_y – діапазон С4:С14, изв_знач_x – діапазон A4:A14.

З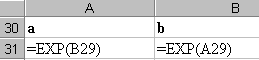 а отриманими параметрами регресії для “лінеаризованої” моделі знаходимо параметри для початкової нелінійної моделі. Для цього у клітини A31, B31 вводимо формули, що показані на малюнку.

Д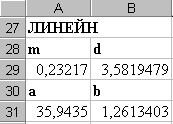 алі наведено вигляд робочого аркушу з отриманими параметрами регресії для “лінеаризованої” та початкової моделі з використанням функції ЛИНЕЙН(.). Значення в клітинах A31, B31 (див. малюнок) співпадають зі значеннями у клітинах A20, B20, що містять параметри регресії обчислені за функцією ЛГРФПРИБЛ(.).

Використовуючи значення у клітинах A29, B29 або A31, B31 можна визначити апроксимації відповідно для величин або .

Апроксимації для названих величин можна також отримати за допомогою функції ТЕНДЕНЦИЯ(.), використовуючи “лінеаризовану модель”. Для цього виділяємо діапазон I4:I15, вводимо знак “=”, aктивізуємо засіб Мастер функций. У вікнах діалогів Мастер функций вибираємо функцію ТЕНДЕНЦИЯ(.) та задаємо її аргументи: изв_знач_y – діапазон С4:С14, изв_знач_x – діапазон A4:A14 ; нов_знач_x – A4:A15. Після натискання комбінації клавіш CTRL+SHIFT+ENTER одержуємо результат, що є апроксимацією для величин .

Далі виділяємо діапазон J4:J15, вводимо знак формулу “=EXP(I4:I15)” та натискаємо комбінацію клавіш CTRL+SHIFT+ENTER. В результаті одержуємо апроксимацію величин , що співпадає з апроксимацією, обчисленою за формулою РОСТ(.) (діапазон E4:E15).