
- •План виконання лабораторної роботи
- •Теоретичні відомості
- •Впливові та залежні клітини
- •Перегляд впливових та залежних клітин на робочих аркушах
- •Призначення кнопок на панелі інструментів Зависимости
- •Використання засобу Подбор параметра
- •Використання засобу Диспетчер сценариев
- •Створення сценарію
- •Редагування сценарію
- •Перегляд сценарію
- •Створення звіту за сценаріями
- •Використання засобу Поиск решения
- •Формування задачі на робочому аркуші
- •Ініціалізація процедури Поиск решения
- •Результати виконання процедури Поиск решения
- •Математична постановка задач
- •Способи розв’язання задач регресійного аналізу у ms Excel
- •Описання вбудованих функцій ms Excel для розв’язання задач регресійного аналізу
- •Специфіка розв’язання задач нелінійної регресії у ms Excel
- •Методичні рекомендації щодо виконання лабораторної роботи
- •Застосування Мастера диаграмм для побудови лінії тренду
- •Використання процедури Поиск решения для обчислення параметрів регресії
- •Використання функції линейн(.) для обчислення параметрів лінійної регресії
- •Використання функції тенденция(.) для обчислення апроксимаційних та прогнозних значень на основі лінійної регресії
- •Аналіз одержаних результатів
- •Використання функцій лгрфприбл(.) та рост(.)
- •Використання процедури Поиск решения для обчислення параметрів регресії
- •Використання функцій линейн(.) та тенденция(.)
- •Аналіз одержаних результатів
- •Контрольні запитання
- •Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Завдання 5
- •Завдання 6
- •Завдання 7
- •Завдання 8
- •Завдання 9
- •Завдання 10
- •Завдання 11
- •Завдання 12
- •Завдання 13
- •Завдання 14
- •Завдання 15
ЗМІСТ
ВСТУП 3
ЛАБОРАТОРНА РОБОТА 5
План виконання лабораторної роботи 5
Теоретичні відомості 7
Математична постановка задач аналізу 7
Інтерпретація задач у термінах залежних та впливових клітин та засоби MS Excel для їх розв’язання 9
Задачі регресійного аналізу 17
Методичні рекомендації щодо виконання лабораторної роботи 24
Завдання 1 (лінійна регресія) 24
Хід виконання 25
Завдання 2 (нелінійна регресія) 33
Хід виконання 33
Висновки 37
Контрольні запитання 38
Індивідуальні завдання 38
СПИСОК ЛІТЕРАТУРИ 47
ВСТУП
Особливість електронних таблиць MS Excel полягає в тому, що зміна даних у деяких клітинах книги відображається на інших даних, що містяться в залежних клітинах робочих аркушів. Це дає можливість переглянути альтернативні рішення задачі з метою вибору оптимальних рішень. Але перегляд альтернатив та їх аналіз безпосередньо в клітинах робочого аркушу вельми складна задача. Для спрощення такого аналізу MS Excel пропонує декілька засобів, а саме - Подбор параметра, Диспетчер сценариев та Поиск решения.
Методична розробка містить загальні математичні постановки задач, для розв’язання яких можна застосувати названі засоби MS Excel. Наведено також інтерпретацію задач у термінах залежних та впливових клітин MS Excel і описано технологію їх розв’язання.
Практичне застосування аналітичних засобів MS Excel, зокрема засобу Поиск решения, розглянуто на прикладі знаходження ліній регресій (тренду) різних типів та використання їх для прогнозування. Наведено вигляд оптимізаційних задач регресійного аналізу для різних класів функцій та просторів. Для практичного знаходження ліній тренду вибрано класичну постановку задачі регресійного аналізу на основі евклідової норми. Така задача є задачею мінімізації цільової функції, що виражає суму квадратів відхилень значень лінії апрокcимації від значень базової лінії у точках спостереження. У літературі така постановка задач регресійного аналізу називається методом найменших квадратів.
Крім процедури Поиск решения у своєму арсеналі MS Excel містить ще й інші вбудовані засоби для розв’язання задач регресійного аналізу: засіб Мастер диаграмм для графічного зображення ліній тренду для деяких класів функцій; статистичні функції ЛИНЕЙН(.), ЛГРФПРИБЛ(.) для обчислення параметрів лінійної та показникової регресії; статистичні функції ТЕНДЕНЦИЯ(.), РОСТ(.) для знаходження апроксимаційних та прогнозних значень названих регресій. Всі вони також розглянуті з метою їх порівняння та виявлення серед них найбільш ефективних для розв’язання поставлених задач. Порівняння засобів виконується шляхом аналізу значень цільової функції методу найменших квадратів у розв’язках, що одержуються різними способами. Для аналізу застосовується засіб MS Excel Диспетчер сценариев.
Методична розробка містить також 15 індивідуальних завдань. Завдання створені так, що всі задачі на знаходження ліній регресії, полягають у мінімізації функції двох змінних без обмежень, оскільки розглядається одновимірна регресія на класах простих функцій. З властивостями таких функцій студенти знайомі ще з уроків математики середньої школи.
Під час розв’язання задач для більш глибокого розуміння процесу знаходження параметрів ліній тренду можна скористатися широкими графічними можливостями MS Excel: по-перше, зобразити поверхність цільової функції та провести попередній аналіз оптимізаційної задачі; по-друге, на графік, що містить базову лінію, додати лінію апроксимації для початкових значень параметрів та простежити процес знаходження оптимальних значень параметрів на ітераціях процедури Поиск решения; по-третє, візуально порівняти графіки ліній тренду, що одержані, різними способами.
Пояснення до виконання індивідуальних завдань наведено на прикладах розв’язання задач лінійної та нелінійної регресій з повним використанням графічних та аналітичних засобів MS Excel.
Методична розробка містить рекомендації щодо використання засобів MS Excel для розв’яззання поставлених задач. Зроблені висновки грунтуються на математичних викладках та на результатах аналізу одержаних розв’язків.
Для перевірки засвоєння теоретичного матеріалу та практичних навичків щодо аналізу даних у кінці розробки наведено перелік контрольних запитань.
Теоретичний та практичний матеріал, що розглядається, призначений для поглибленого вивчення можливостей MS Excel та застосування його для аналізу даних. Він розрахованих на студентів, які володіють основами математики на стільки, щоб зрозуміти математичні постановки задач оптимізації, знають основні прийоми роботи у табличному процесорі МS Excel, вміють користуватися такими його засобами: Мастер функции, Мастер диаграмм, Таблица подстановки.
Методичну розробку можна використати для проведення лабораторної роботи з дисципліни “Інформатика та комп’ютерна техніка” або з дисципліни “Інформаційні системи” під час вивчення додаткових можливостей табличного процесора MS Excel. Студентам старших курсів можна запропонувати ускладнені індивідуальні завдання, розглянувши багатовимірну регресію.
ЛАБОРАТОРНА РОБОТА
Тема: Табличний процесор MS Excel. Елементи прогнозування.
Мета: Набути практичних навичок щодо використання засобів MS Excel для розв’язання задач регресійного аналізу. Навчитися використовувати вбудовані функції ЛИНЕЙН(.), ЛГРФПРИБЛ(.), ТЕНДЕНЦИЯ(.), РОСТ(.) для обчислення параметрів регресії та прогнозних значень. Вміти застосовувати Мастер диаграмм для побудови ліній тренду різних типів. Одержати практичні навички щодо формування оптимізаційної задачі регресійного аналізу та розв’язання її за допомогою засобу MS Excel Поиск решения.
План виконання лабораторної роботи
У
табличному процесорі МS Excel,
використовуючи дані індивідуального
завдання, проаналізувати зміни залежної
величини
![]() від незалежної змінної
від незалежної змінної
![]() , i=1,…n
та
спрогнозувати значення
, i=1,…n
та
спрогнозувати значення
![]() для деякого значення
для деякого значення
![]() .
(Тип регресії див. у індивідуальному
завданні). Для розв’язання задач
регресійного аналізу необхідно
використати такі засоби MS
Excel:
.
(Тип регресії див. у індивідуальному
завданні). Для розв’язання задач
регресійного аналізу необхідно
використати такі засоби MS
Excel:
Засіб Мастер диаграмм, якщо використовується одновимірна регресія на класах лінійних, логарифмічних, експоненціальних, степеневих, поліноміальних функцій (вигляд функцій наведено нижче).
Засіб Поиск решения. Розв’язання задачі виконати за такою схемою:
Сформувати цільову функцію оптимізаційної задачі для розрахунків параметрів регресії методом найменших квадратів;
Побудувати таблицю значень цільової функції оптимізаційної задачі для різних значень параметрів регресії, якщо параметрів небільше, ніж 2. (Примітка. Цільова функція оптимізаційної задачі матиме два аргументи для одновимірної регресії на всіх класах функцій, що наведені у п.1, крім поліноміальних. Для поліноміальних кількість аргументів цільової функції залежить від степеню полінома);
Виконати попередній аналіз цільової функції оптимізаційної задачі за допомогою Мастера диаграмм – побудувати поверхню цільової функції для різних значень параметрів регресії, якщо параметрів небільше, ніж 2. (Виконується для одновимірної регресії на всіх класах функцій, що наведені у п.1, крім поліноміальних);
З використанням Мастера диаграмм побудувати базову лінію залежної змінної
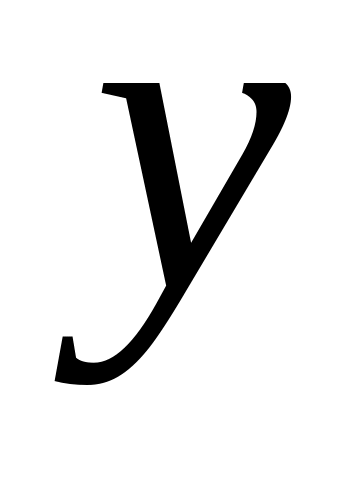 ,
якщо розглядається одновимірна
регресія. На графік
додати лінію регресії для початкових
значень параметрів (за початкові
значення взяти будь-які числа).
,
якщо розглядається одновимірна
регресія. На графік
додати лінію регресії для початкових
значень параметрів (за початкові
значення взяти будь-які числа).
За допомогою процедури Поиск решения обчислити оптимальні значення параметрів регресії.
Використовуючи параметри регресії, обчислити прогнозні значення залежної змінної .
Вбудовані функції ЛИНЕЙН(.), ТЕНДЕНЦИЯ(.), якщо розглядається лінійна регресія. Для розв’язання задач регресійного аналізу на класах нелінійних функцій (експоненціальних, логарифмічних показникових тощо) необхідно початкову нелінійну модель замінити на “лінеаризовану”, використовуючи математичні перетворення. За одержаними параметрами регресії для “лінеаризованої” моделі обчислити наближені значення регресії для початкової нелініної моделі.
Вбудовані функції ЛГРФПРИБЛ(.), РОСТ(.), якщо розглядається показникова регресія.
Провести порівняння та аналіз результатів, що одержані різними способами. Для аналізу використати засоби MS Excel Диспетчер сценариев та Мастер диаграмм.
Теоретичні відомості
Математична постановка задач аналізу
Н ехай
існує деяка функціональна залежність
між незалежною змінною
ехай
існує деяка функціональна залежність
між незалежною змінною
![]() та
залежною змінною
:
та
залежною змінною
:
![]() .
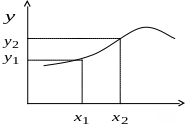
На малюнку таку залежність
можна зображено графіком.
.
На малюнку таку залежність
можна зображено графіком.
Р
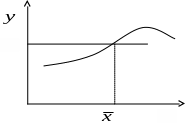 озглянемо
задачу, яка полягає в наступному: знайти
таку точку
озглянемо
задачу, яка полягає в наступному: знайти
таку точку
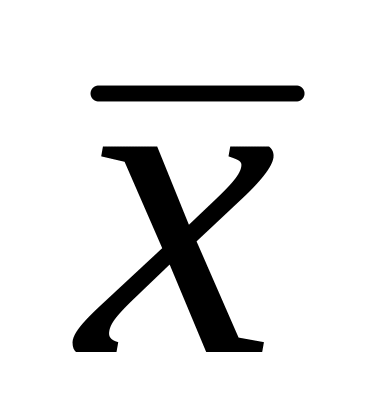 ,
для якої
,
для якої
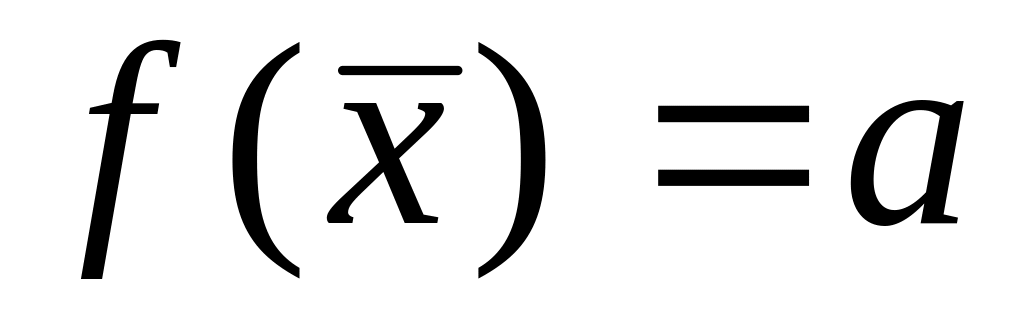 ,
де
,
де
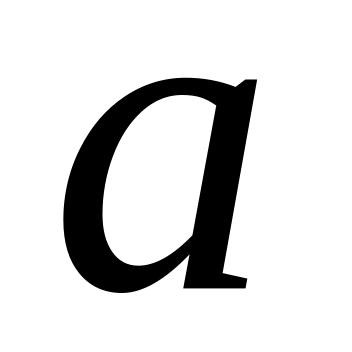 –
деяке задане число. На малюнку це означає
–
знайти точку перетину графіка функції
з прямою
–
деяке задане число. На малюнку це означає
–
знайти точку перетину графіка функції
з прямою
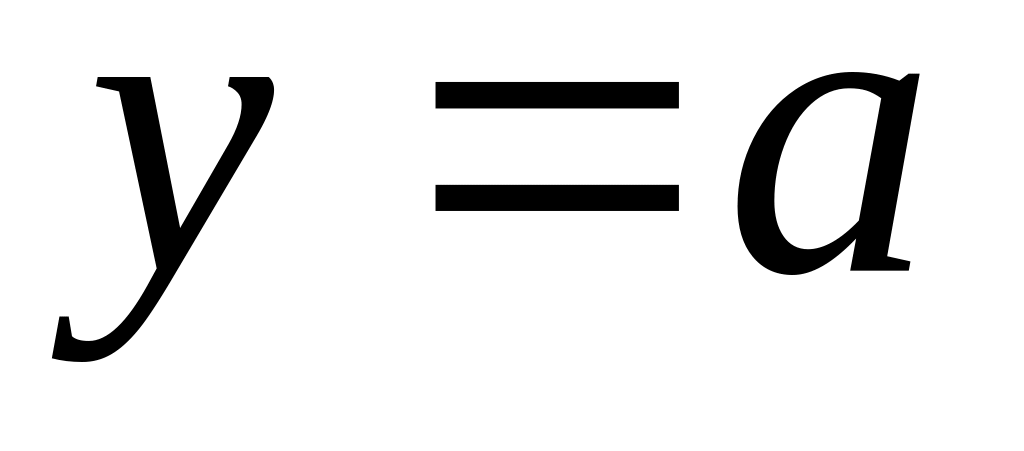 .
.
Залежно
від вигляду функції
![]() та значень
задача може не мати розв’язку.
та значень
задача може не мати розв’язку.
Якщо
функція
– функція однієї змінної, тобто
![]() ,
то для її розв’язання можна скористатися
засобом MS Excel
Подбор параметра.
,
то для її розв’язання можна скористатися
засобом MS Excel
Подбор параметра.
Р
 озглянемо
обернену задачу. Нехай відомі деякі
значення незалежної змінної
озглянемо
обернену задачу. Нехай відомі деякі
значення незалежної змінної
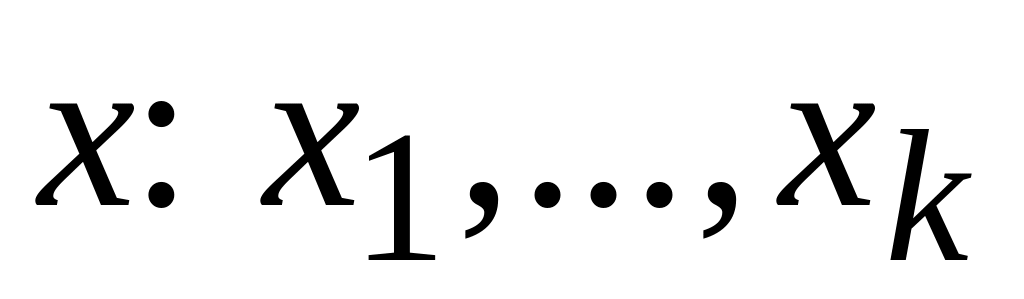 .
Потрібно знайти (див. малюнок) та
проаналізувати значення
.
Потрібно знайти (див. малюнок) та
проаналізувати значення

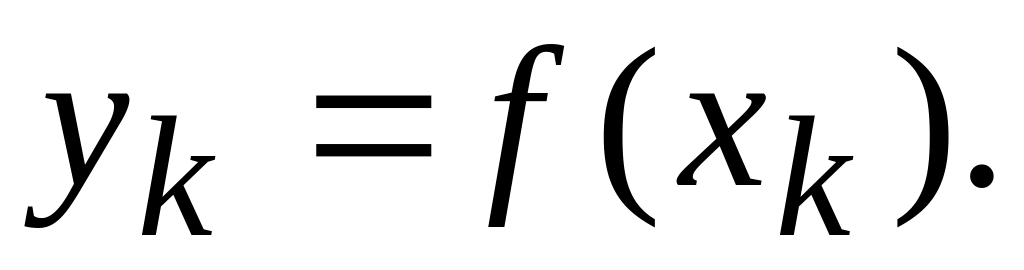
Таку
задачу в MS Excel
можна
вирішити з використанням Диспетчера
сценариев.
При цьому припускається, що
– функція багатьох змінних, тобто
![]() .
Можна також одночасно аналізувати
значення декількох функцій (кількість
функцій не повинна перевищувати 32).
.
Можна також одночасно аналізувати
значення декількох функцій (кількість
функцій не повинна перевищувати 32).
Розглянемо задачі.
а) Знайти
точку
![]() таку, що
таку, що
![]() для всіх
.
Це означає, що в точці
значення залежної змінної
для всіх
.
Це означає, що в точці
значення залежної змінної
![]() є максимальним, тобто
–
розв’язок
задачі
максимізації:
є максимальним, тобто
–
розв’язок
задачі
максимізації:
![]() .
.
б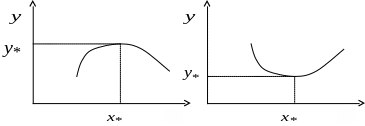 ) Знайти
точку
) Знайти
точку
![]() таку, що
таку, що
![]() для всіх
.
Це означає, що в точці
значення залежної змінної
є мінімальним, тобто
– розв’язок задачі мінімізації:
для всіх
.
Це означає, що в точці
значення залежної змінної
є мінімальним, тобто
– розв’язок задачі мінімізації:
![]() .
.
На малюнках зображено знаходження точок максимуму та мінімуму.
в) Знайти
точку
![]() таку,
що
,
де
–
деяке задане число. Ця задача є
узагальненням задачі 1, оскільки
припускається, що
–функція багатьох змінних, тобто
таку,
що
,
де
–
деяке задане число. Ця задача є
узагальненням задачі 1, оскільки
припускається, що
–функція багатьох змінних, тобто
![]() .
.
Для всіх
трьох випадків а) –
в) можуть існувати додаткові обмеження
на незалежну змінну
,
тобто вимога того, що
![]() ,
де
,
де
![]() –
деяка множина. У цьому випадку задачі
3а), 3б) називаються задачами умовної
оптимізації і записуються так:
–
деяка множина. У цьому випадку задачі
3а), 3б) називаються задачами умовної
оптимізації і записуються так:
![]() .
.
Для задач оптимізації функція називається цільовою функцією, множина – допустимою множиною, – допустимою точкою, – оптимальною точкою.
Множина
задається системою рівностей та
нерівностей
![]() ,
де
,
де
![]() та
та
![]() –
деякі функції.
–
деякі функції.
Множина
може включати прості обмеження на
компоненти незалежної змінної, наприклад,
![]() або
або
![]() ,
де
,
де
![]() –
деякі числа.
–
деякі числа.
Якщо
функції
![]() є лінійними, то задачі 3а), 3б) називаються
задачами лінійного програмування. У
протилежному випадку вони називаються
задачами нелінійної оптимізації.
є лінійними, то задачі 3а), 3б) називаються
задачами лінійного програмування. У
протилежному випадку вони називаються
задачами нелінійної оптимізації.
Якщо існує обмеження на цілочисленість незалежної змінної , то задачі 3а), 3б) називаються задачами цілочисленого математичного програмування.
Для розв’язання оптимізаційних задач можна застосувати засіб MS Excel Поиск решения. У MS Excel щодо застосування процедури Поиск решения існують такі вимоги на вимірність задачі:
вимірність простору незалежної змінної не може перевищувати 200, тобто
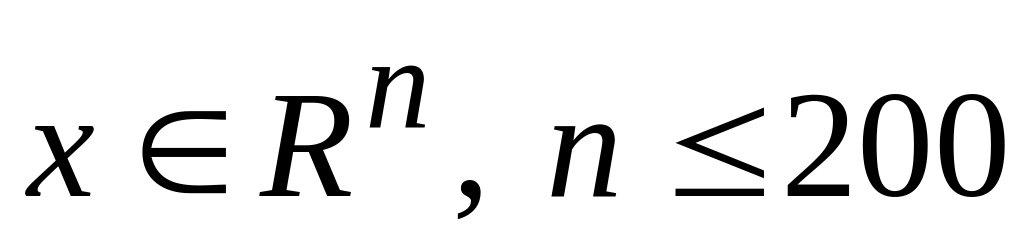 ;
;кількість функціональних обмежень, що визначають множину , не може перевищувати 100, тобто
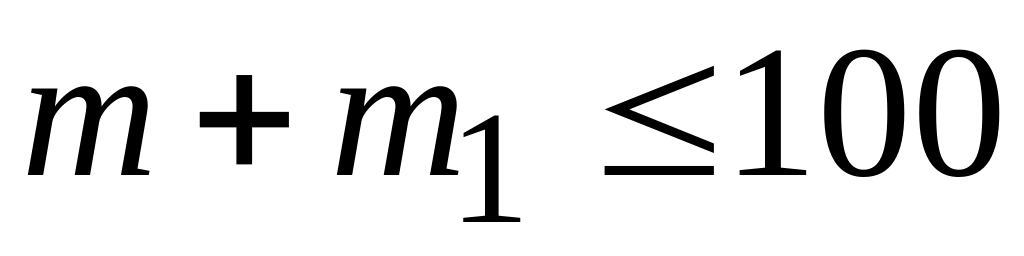 ;
;може існувати по два простих обмеження для кожної компоненти незалежної змінної .
Інтерпретація задач у термінах залежних та впливових клітин та засоби MS Excel для їх розв’язання
