4. Линейные дифференциальные уравнения - го порядка.

Линейное дифференциальное уравнение - го порядка с постоянными коэффициентами имеет вид:

, (20)

где , - вещественные числа, - заданная функция.

Уравнение (20) называется однородным (сокращенно ЛОДУ), если правая часть , в противном случае уравнение (20) называется неоднородным (сокращенно ЛНДУ).

Уравнение

(21)

называется ЛОДУ, соответствующим данному ЛНДУ (20).

Общее решение уравнения (20) может быть представлено в виде суммы , где - общее решение соответствующего ЛОДУ, а - любое частное решение ЛНДУ.

Алгебраическое уравнение вида

(22)

называется характеристическим уравнением ЛОДУ (21). Левая часть уравнения (22) представляет собой полином - ой степени относительно . Корни характеристического уравнения называются характеристическими числами ЛОДУ. Число , для которого , называется простым корнем уравнения (22). Число , для которого , где , называется корнем кратности уравнения (22).

Рассмотрим сначала ЛОДУ 2-го порядка:

(23)

Тогда характеристическое уравнение (22) имеет вид:

(24)

В этом случае общее решение уравнения (23) в зависимости от вида корней характеристического уравнения (24) имеет следующий вид:

1) если - вещественны и различны ( ), то

2) если - вещественны и , то

3) если - комплексно сопряженные числа, то

.

В общем случае ЛОДУ - го порядка вид общего решения также определяется видом корней характеристического уравнения. Если уравнение (22) имеет действительных корней кратностей и пар комплексно сопряженных корней кратностей , , то общее решение ЛОДУ (21) имеет вид:

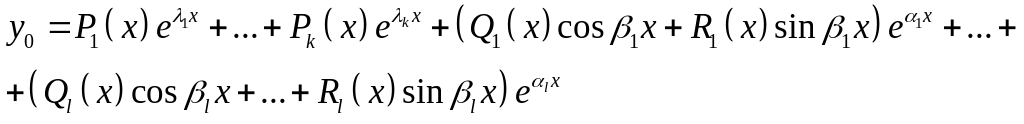
где - многочлен степени , а - многочлены степени , коэффициентами которых являются произвольные постоянные .

Частное решение ЛНДУ (20) в случае, когда правая часть уравнения имеет специальный вид:

, (25)

где и - многочлены степени и соответственно, ищется в виде:

, (26)

где и - многочлены степени с неопределенными коэффициентами, а - кратность чисел как корней характеристического уравнения (22).

Задание. Найти решение уравнения , удовлетворяющее условиям: .

Решение. Характеристическое уравнение данного дифференциального уравнения имеет вид:

Его корни - комплексно сопряженные числа. Следовательно, общее решение соответствующего ЛОДУ имеет вид:

.

Найдем теперь частное решение ЛНДУ. Правая часть уравнения имеет специальный вид (25): . Следовательно, . Тогда - простые корни характеристического уравнения, то есть . Таким образом, частное решение данного ЛНДУ будем искать в виде (26):

.

Подставляем и в исходное ЛНДУ, получаем:

.

Приравнивая коэффициенты при косинусах и синусах, находим:

.

Следовательно,

- частное решение ЛНДУ.

Тогда общее решение исходного линейного неоднородного дифференциального уравнения имеет вид:

.

Осталось найти решение задачи Коши: . Подставляя начальные данные в формулы для и , находим:

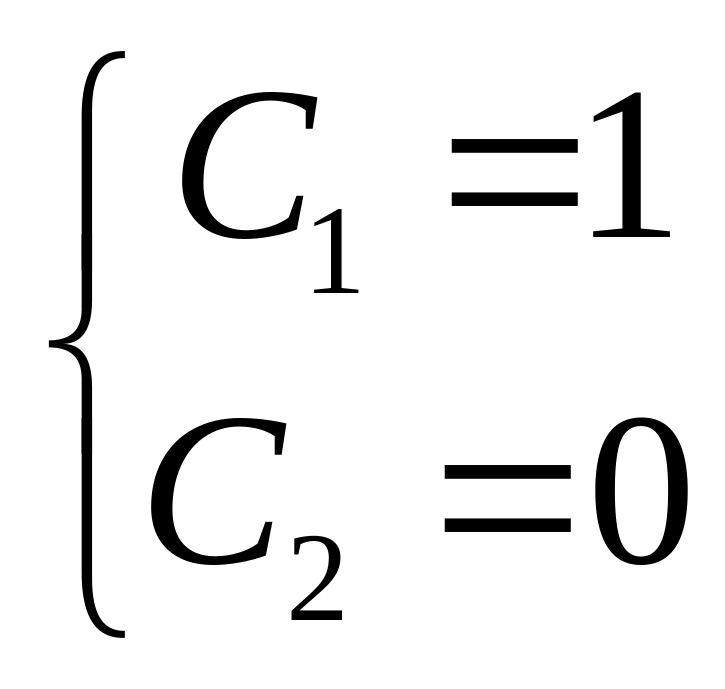
Следовательно, решением поставленной задачи Коши будет функция

.

В общем случае для нахождения решения ЛНДУ (20) можно воспользоваться методом вариации произвольных постоянных. Рассмотрим этот метод сначала на примере.

Задание. Решить уравнение: .

Решение. Найдем сначала решение соответствующего ЛОДУ. Характеристическое уравнение имеет вид:

.

Оно имеет один корень кратности 2. Следовательно, общее решение ЛОДУ имеет вид:

.

Функции и - линейно независимые решения ЛОДУ. Общее решение исходного ЛНДУ будем искать в виде:

, (27)

где - неизвестные функции, которые находятся из системы:

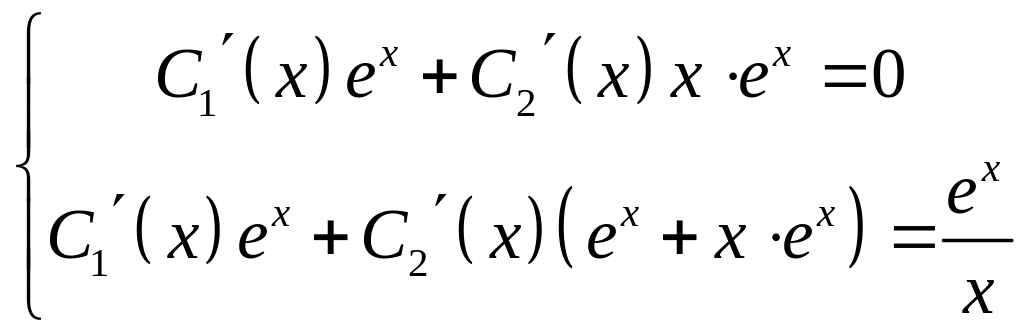. (28)

Система (28) – линейная алгебраическая система с неизвестными , определитель которой равен

.

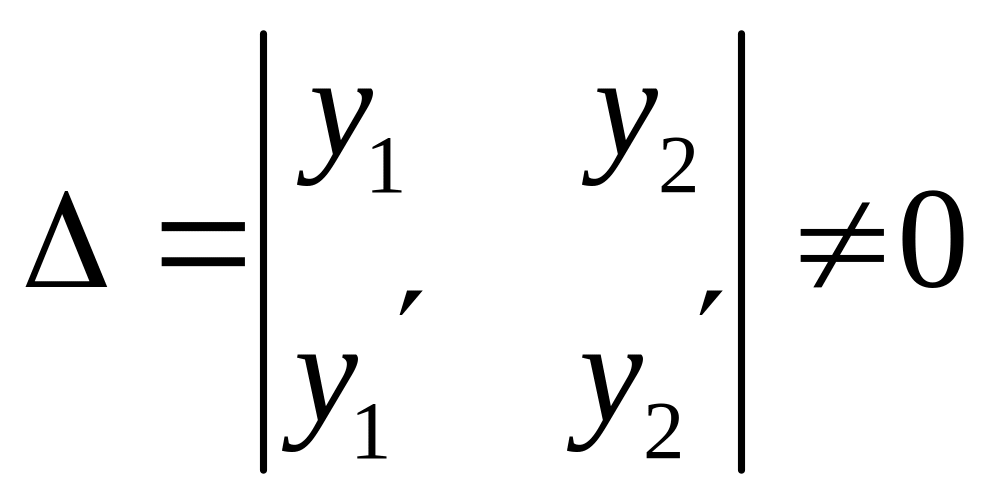Решив систему (28), получим:

.

Интегрируя последние равенства, находим:

.

Подставим найденные функции в формулу (27). Таким образом, общее решение исходного уравнения имеет вид:

.

В общем случае метод вариации произвольных постоянных может применяться к ЛНДУ с произвольными коэффициентами вида:

, (29)

где - непрерывные функции. Соответствующее ЛОДУ имеет вид:

. (30)

Функции называются линейно зависимыми на промежутке , если существуют постоянные , не все равные нулю, такие, что:

при .

В противном случае данные функции называются линейно независимыми на промежутке .

Совокупность линейно независимых решений ЛОДУ (30) называется фундаментальной системой решений данного ЛОДУ. Для того, чтобы решений ЛОДУ были линейно независимы на промежутке , необходимо и достаточно, чтобы определитель

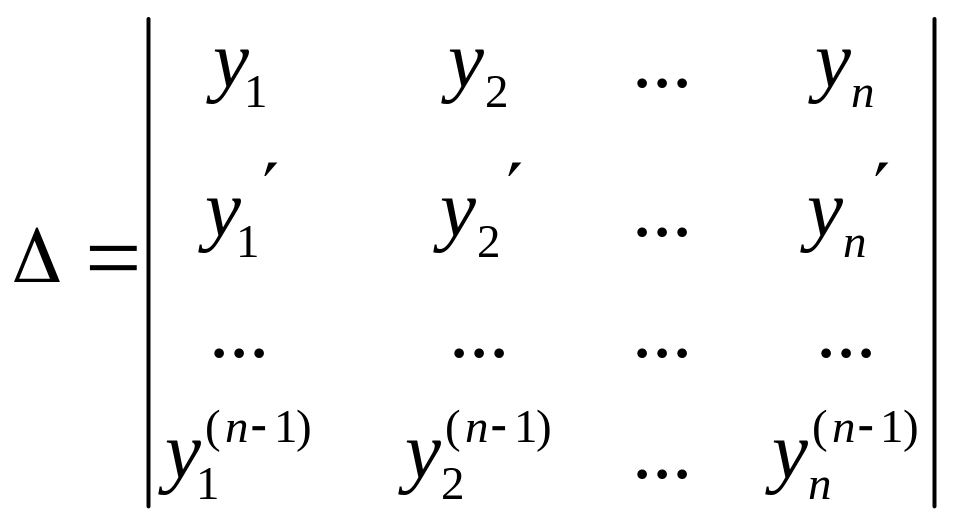
был отличен от 0 хоть в одной точке промежутка .

Пусть функции образуют фундаментальную систему ЛОДУ (30). Тогда общее решение этого ЛОДУ может быть записано в виде:

,

где - произвольные постоянные. Тогда общее решение ЛНДУ (29) может быть получено в виде:

, (31)

где - неизвестные функции, которые находятся из системы:

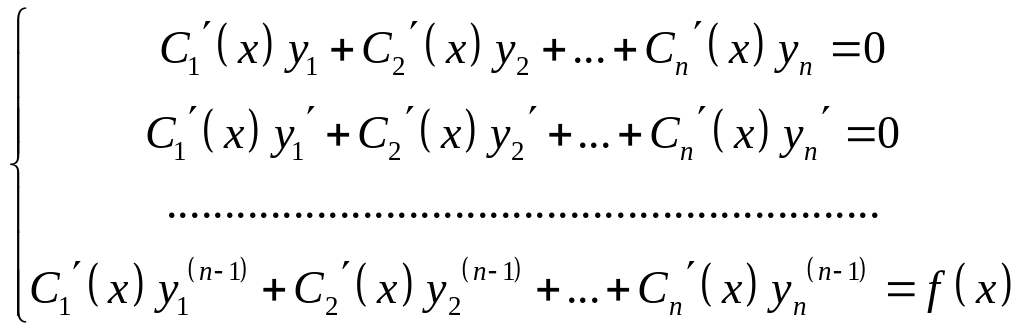(32)

Система (32) – линейная алгебраическая система с неизвестными , определитель которой отличен от 0. Следовательно, система (32) имеет единственное решение. Решив систему (32), находим , следовательно, и (см. предыдущий пример). Подставляя найденные функции в формулу (31), получаем общее решение ЛНДУ (29).