
- •Высшая математика
- •Введение
- •Глава I. Неопределенные и определенные интегралы
- •1.Неопределенный интеграл
- •Непосредственное интегрирование.
- •Интегралы вида .
- •Интегралы вида
- •Основные методы вычисления определенных интегралов
- •Формула Ньютона – Лейбница.
- •2.Замена переменной в определенном интеграле.
- •Интегрирование по частям в определенном интеграле.
- •3. Несобственные интегралы
- •4. Приложения определенных интегралов
- •Глава 2. Дифференциальные уравнения
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Дифференциальные уравнения первого порядка Дифференциальные уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка. Уравнение Бернулли
- •3. Дифференциальные уравнения, допускающие понижение порядка Уравнение вида .
- •Уравнение вида .
- •4. Линейные дифференциальные уравнения - го порядка.
- •5. Системы дифференциальных уравнений
- •Глава 3. Дифференциальное исчисление функций многих переменных
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Предел и непрерывность функции
- •Частные производные. Дифференциал функции
- •Производная в данном направлении. Градиент
- •Экстремумы функции нескольких переменных
- •Оглавление
- •Глава I. Неопределенные и определенные интегралы………….…3
- •3. Несобственные интегралы ……………………………………………….15
- •4. Приложения определенных интегралов ………………………………...17
- •Глава II. Дифференциальные уравнения ……………………………...18
- •Глава III. Дифференциальное исчисление функций многих переменных ……………………………………………………………………31
Непосредственное интегрирование.
Отыскание неопределенного интеграла с помощью свойств неопределенных интегралов, таблицы основных интегралов и тождественных преобразований выражений называют непосредственным интегрированием.
Метод подстановки (замены переменной).
Пусть требуется
вычислить интеграл
,
где функция
определена на некотором промежутке
.
Сделаем замену переменной в подынтегральном
выражении, положив
![]() ,
где
,
где
![]() -
новая переменная,
-
новая переменная,
![]() -
функция, определенная и непрерывно
дифференцируемая на некотором промежутке
-
функция, определенная и непрерывно
дифференцируемая на некотором промежутке
![]() .
Тогда получим:
.
Тогда получим:
![]() ,
(1)
,
(1)
причем после
вычисления интеграла правой части (1)
возвращаются к старой переменной
![]() обратной подстановкой
обратной подстановкой
![]() .
.
Заметим, что функцию выбирают таким образом, чтобы интеграл в правой части равенства (1) оказался проще исходного и мог быть вычислен.
3.Метод интегрирования по частям.
Если функции
![]() и
и
![]() -
дифференцируемые, то справедлива
формула:
-
дифференцируемые, то справедлива
формула:
![]() (2)
(2)
Заметим, что функции
и
![]() выбирают таким образом, чтобы интеграл
в правой части формулы (2) оказался проще
исходного. Иногда формулу интегрирования
по частям (2) приходится применять
несколько раз.
выбирают таким образом, чтобы интеграл
в правой части формулы (2) оказался проще
исходного. Иногда формулу интегрирования
по частям (2) приходится применять
несколько раз.
Интегрирование рациональных функций
Дроби вида
![]() и
и
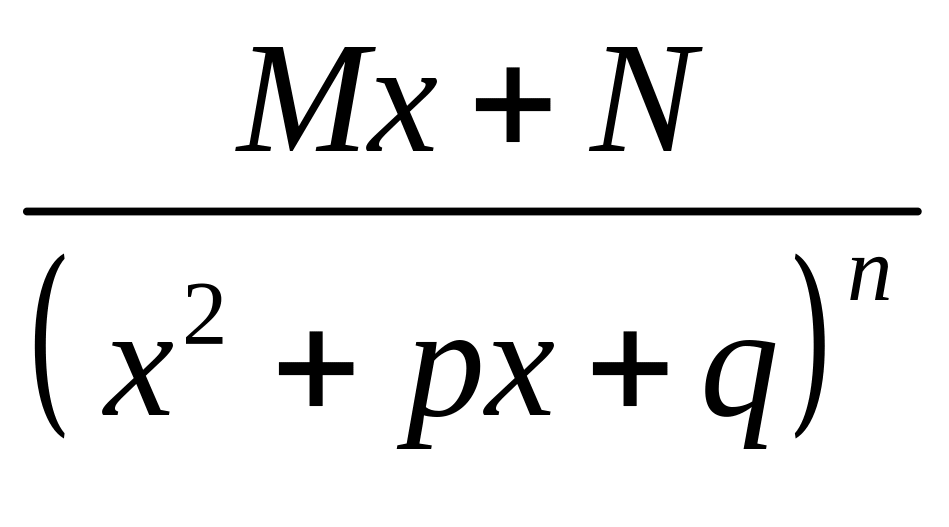 ,
где
,
где
![]() и
и
![]() ,
называют простейшими
дробями соответственно 1 и 2 типов.
Интегралы от простейших дробей вычисляются
изложенными выше методами.
,
называют простейшими
дробями соответственно 1 и 2 типов.
Интегралы от простейших дробей вычисляются
изложенными выше методами.
Интегрирование
рациональных функций вида
![]() сводится к интегрированию простейших
дробей. Возможны два случая:
сводится к интегрированию простейших
дробей. Возможны два случая:
Пусть
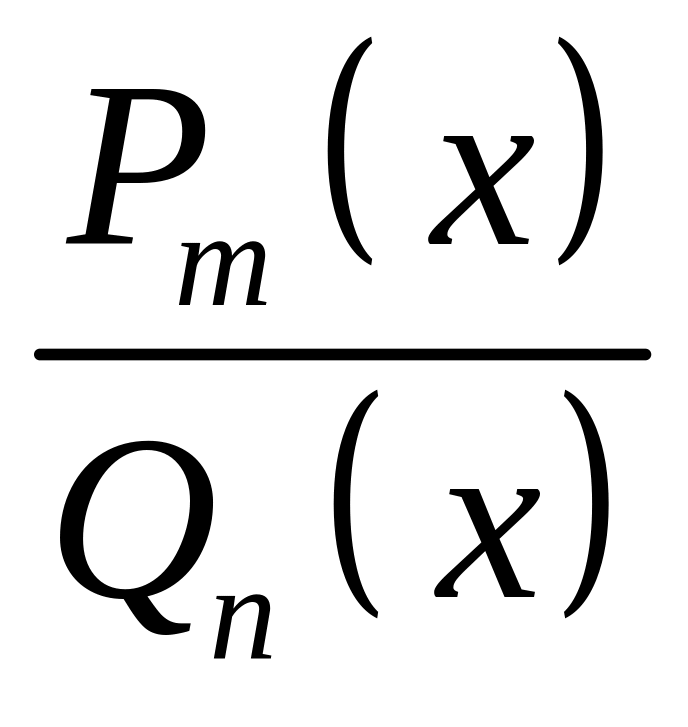 -
правильная
-
правильная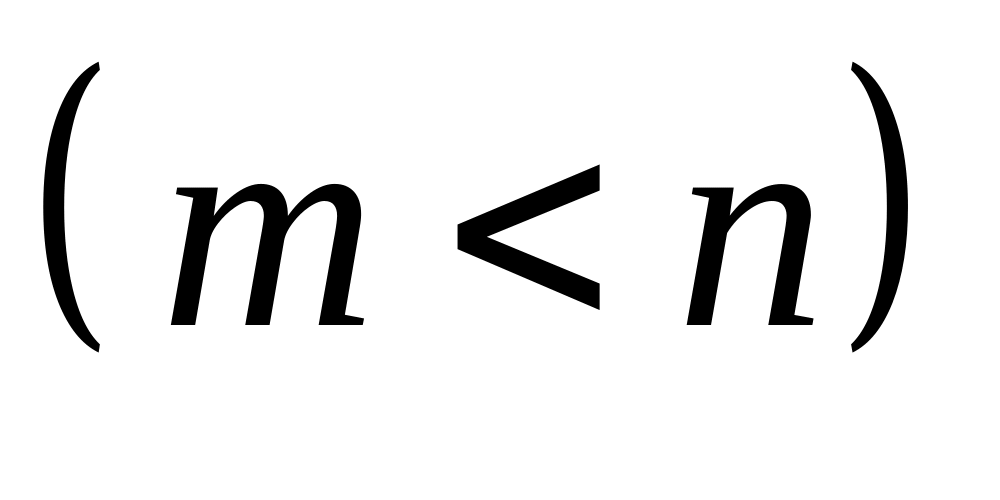 рациональная
функция,
причем
рациональная
функция,
причем
![]() ,
,
и
![]() .
Тогда дробь
представима в виде суммы простейших
дробей 1 и 2 типов:
.
Тогда дробь
представима в виде суммы простейших
дробей 1 и 2 типов:
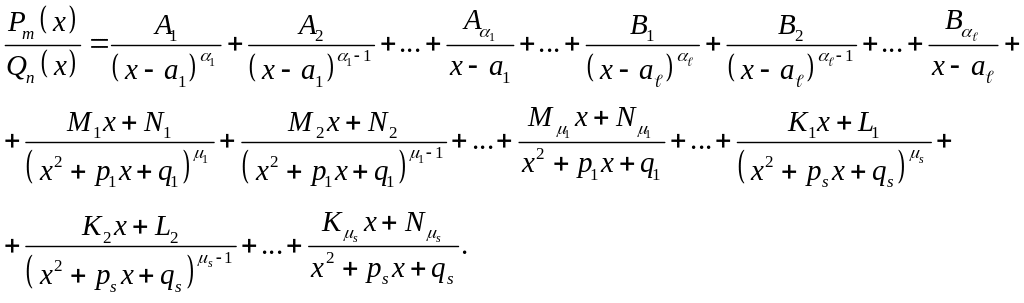
Если исходная дробь - неправильная
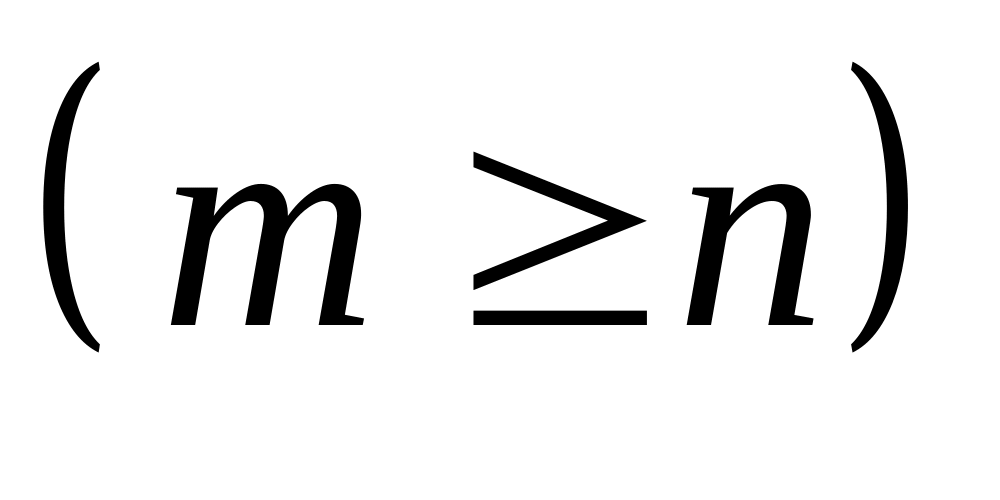 ,
то ее можно представить в виде суммы
многочлена и правильной дроби:
,
то ее можно представить в виде суммы
многочлена и правильной дроби:
![]() .
.
Здесь
![]() - многочлен, дробь
- многочлен, дробь
![]() - правильная (
- правильная (![]() ).
Выделение целой части
дроби
производится делением многочлена
).
Выделение целой части
дроби
производится делением многочлена
![]() на многочлен
на многочлен
![]() (по правилу деления многочленов).
(по правилу деления многочленов).
Таким образом, интегрирование любой рациональной функции сводится к интегрированию многочлена и нескольких простейших дробей.
Интегрирование тригонометрических функций
Интегралы вида .
Рассмотрим интеграл
вида
,
где
![]() -рациональная
функция своих аргументов. С помощью
подстановки
-рациональная
функция своих аргументов. С помощью
подстановки
![]() данный интеграл сводится к интегралу
от рациональной функции переменной
.
Справедливы формулы:
данный интеграл сводится к интегралу
от рациональной функции переменной
.
Справедливы формулы:
![]() .
.
Заметим, что
подстановка
![]() является универсальной, так как дает
возможность проинтегрировать любую
функцию вида
.
Однако на практике иногда эта подстановка
приводит к очень громоздким вычислениям.
Поэтому в некоторых частных случаях
удобнее использовать другие подстановки:
является универсальной, так как дает
возможность проинтегрировать любую
функцию вида
.
Однако на практике иногда эта подстановка
приводит к очень громоздким вычислениям.
Поэтому в некоторых частных случаях
удобнее использовать другие подстановки:
а) Пусть интеграл
имеет вид
![]() или
или
![]() .
Тогда соответственно применяется замена
.
Тогда соответственно применяется замена
![]() или
или
![]() ,
которая приводит рассматриваемый
интеграл к интегралу от рациональной
функции нового аргумента
.
,
которая приводит рассматриваемый
интеграл к интегралу от рациональной
функции нового аргумента
.
б) Если
подынтегральная функция имеет вид
,
но
![]() и
и
![]() содержатся только в четных степенях,
то удобнее воспользоваться подстановкой
содержатся только в четных степенях,
то удобнее воспользоваться подстановкой
![]() ,
в результате которой получим интеграл
от рациональной функции переменной
.
,
в результате которой получим интеграл
от рациональной функции переменной
.
в) Пусть
![]() .
Тогда возможны 3 случая:
.
Тогда возможны 3 случая:
1) Пусть среди
чисел
![]() и
и
![]() есть хотя бы одно нечетное число.
Допустим, для определенности, что
-
нечетное, т.е.
есть хотя бы одно нечетное число.
Допустим, для определенности, что
-
нечетное, т.е.
![]() .
Тогда, представив
.
Тогда, представив
![]() и положив
,
приходим к интегралу, который легко
вычисляется.
и положив
,
приходим к интегралу, который легко
вычисляется.
2) Пусть числа
и
- четные и неотрицательные. Тогда с
помощью формул
![]() и
и
![]() можно понизить степени синуса и косинуса
под знаком интеграла:
можно понизить степени синуса и косинуса
под знаком интеграла:
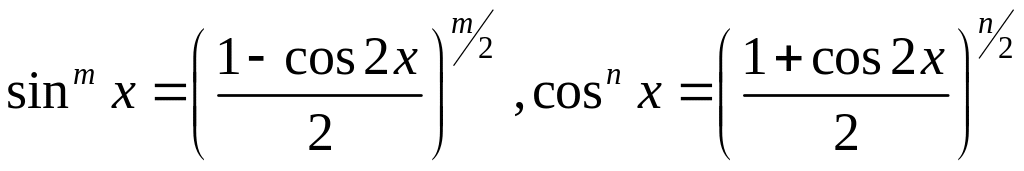 ;
;
3) Пусть оба
показателя степени
и
четные, причем хотя бы один из них
отрицателен. В этом случае следует
сделать замену
или
![]() ,
в результате которой придем к интегралу,
который легко вычисляется.
,
в результате которой придем к интегралу,
который легко вычисляется.
2.
Интегралы вида
![]() или
или
![]() .
.
Для вычисления данных интегралов используют подстановки или , которые приводят рассматриваемые интегралы к интегралам от рациональных функций нового аргумента .
