Глава 2. Дифференциальные уравнения

Теоретические вопросы

1. Основные понятия.

2. Уравнения с разделяющимися переменными.

3. Однородные уравнения.

4. Линейные уравнения. Уравнение Бернулли.

5. Уравнения, допускающие понижение порядка.

6. Линейные однородные уравнения с постоянными коэффициентами.

7. Линейные неоднородные уравнения с постоянными коэффициентами.

8. Метод вариации произвольных постоянных.

9. Системы дифференциальных уравнений.

Литература

1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.

2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.: Высш. шк., 1998. Ч. 1,2.

1. Основные понятия

Дифференциальным уравнением называется уравнение, связывающее независимую переменную , искомую функцию и её производные

(1)

Порядок наивысшей производной, входящей в данное уравнение, называется порядком дифференциального уравнения.

Функция называется решением дифференциального уравнения (1) на промежутке , если уравнение (1) при подстановке в него функции вместе со своими производными обращается в тождество:

.

Общим решением дифференциального уравнения (1) называется функция , (2)

зависящая от переменой и произвольных постоянных и удовлетворяющая следующим условиям:

1. при любых значениях произвольных постоянных 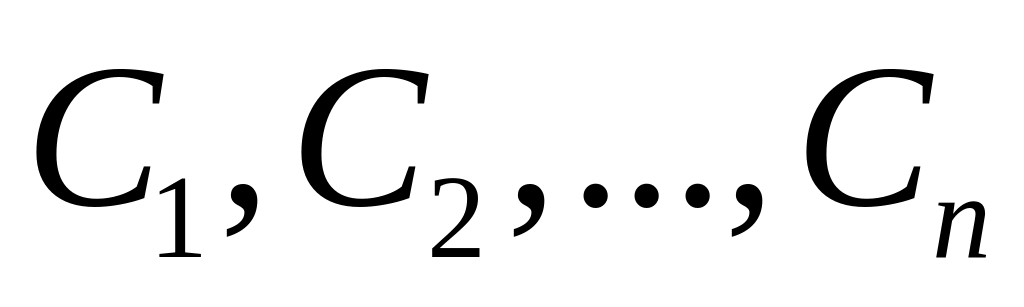функция (2) является решением уравнения (1);

2. любое решение уравнения (1) может быть получено из функции (2) при соответствующих значениях постоянных .

Уравнение , определяющее общее решение уравнения (1) как неявную функцию, называется общим интегралом дифференциального уравнения (1).

Задача нахождения решения уравнения (1), удовлетворяющего начальным условиям:

,

где - заданные числа называется задачей Коши.

2. Дифференциальные уравнения первого порядка Дифференциальные уравнения с разделяющимися переменными

Пусть в уравнении

правая часть может быть представлена в виде произведения двух функций, каждая из которых зависит только от одной переменной: . Тогда уравнение можно записать в виде

. (3)

Уравнение вида (3) называется дифференциальным уравнением с разделяющимися переменными.

Разделив это уравнение на и умножив на , придем к уравнению

. (4)

Интегрируя левую часть (4) по , а правую часть - по , приходим к общему интегралу дифференциального уравнения (3).

Однородные уравнения

Однородным дифференциальным уравнением первого порядка называется уравнение, которое может быть приведено к виду

. (5)

С помощью подстановки , где - новая неизвестная функция, однородное уравнение (5) может быть преобразовано в уравнение с разделяющимися переменными вида:

. (6)

Решив уравнение (6), найдем неизвестную функцию , а, следовательно, и решение уравнения (5): .