3. Дифференциальные уравнения, допускающие понижение порядка Уравнение вида .

Общее решение уравнения вида

(13)

получается путем - кратного интегрирования правой части исходного уравнения:

.

Уравнение вида .

Данное уравнение не содержит явно искомую функцию и её производные до -го порядка включительно. С помощью замены , где - новая неизвестная функция, порядок уравнения может быть понижен на единиц. Действительно, в силу замены: . Следовательно, после подстановки значений производных в исходное уравнение получим уравнение -го порядка:

.

Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:

.

Тогда искомую функцию находим из уравнения

,

которое является уравнением вида (13).

Уравнение вида .

Данное уравнение не содержит явно независимую переменную . С помощью замены , где - новая неизвестная функция, порядок уравнения может быть понижен на единицу. Действительно, в силу замены: , и т.д. Следовательно, после подстановки значений производных в исходное уравнение -го порядка

.

Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:

.

Тогда искомую функцию находим из уравнения

,

которое является уравнением с разделяющимися переменными.

Задание 1. Найти решение уравнения: .

Решение. Общее решение данного уравнения может быть получено в результате 2- кратного интегрирования правой части уравнения. Имеем:

.

И далее

.

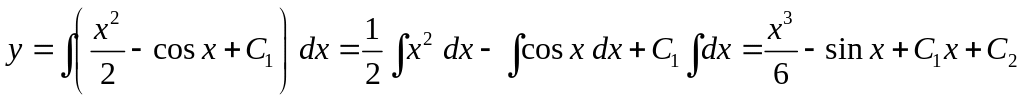Задание 2. Найти решение уравнения: .

Решение. Данное уравнение не содержит явно искомой функции . Следовательно, сделаем замену , где - новая неизвестная функция. Тогда . Подставим полученные значения и в исходное уравнение:

(14)

Уравнение (14) является однородным. Для нахождения его общего решения сделаем замену:

,

или , где - новая неизвестная функция. Тогда: . Подставим значения и в уравнение (14):

,

или

. (15)

Уравнение (15) является уравнением с разделяющимися переменными. Разделив переменные в предположении, что , из (15) имеем:

.

Интегрируя

,

получаем, что .

После преобразования последнего соотношения и обратной замены имеем:

. (16)

Если теперь предположим, что в (15) , то . Следовательно,

,

или

. (17)

Равенство (17) получается из (16) при .

Таким образом, мы получили общее решение уравнения (14):

.

Следовательно, чтобы найти искомую функцию нам надо проинтегрировать функцию :

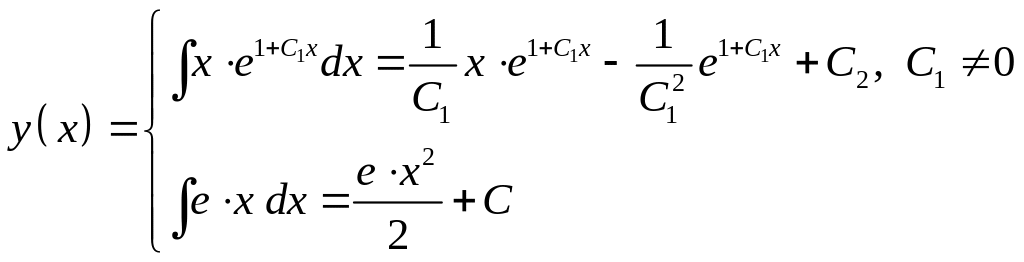
Задание 3. Решить уравнение: .

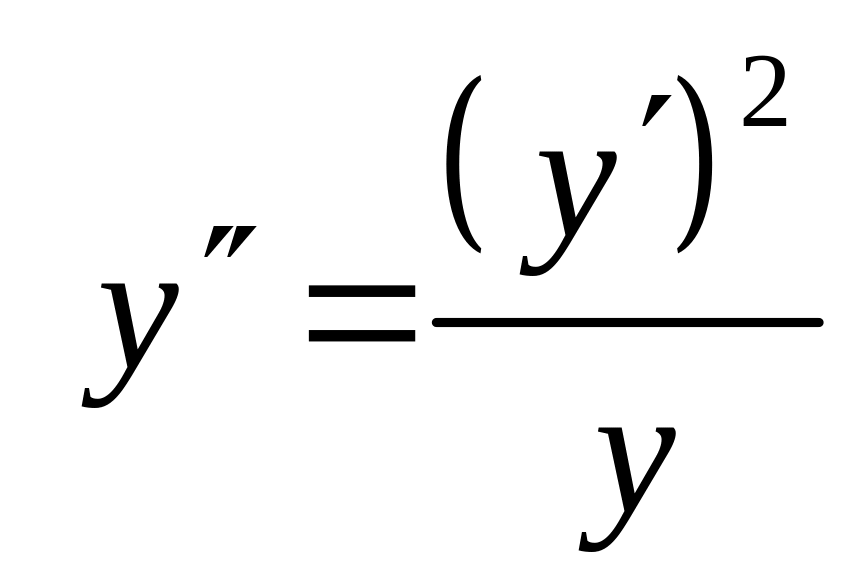Решение. Данное уравнение не содержит явно независимой переменной . Следовательно, замена позволяет понизить порядок исходного уравнения. Действительно, из замены получаем: . Подставляя значения и в данное уравнение, имеем:

. (18)

Полученное уравнение является уравнением с разделяющимися переменными. Если в уравнении (18) , то , т.е. .

Если , то после деления на получаем:

,

или

. ( 19)

Интегрируя (19), находим общее решение уравнения (18) в случае :

,

или

.

Тогда искомая функция исходного уравнения ищется как решение уравнения:

,

которое является уравнением с разделяющимися переменными. Имеем:

.

Интегрируя последнее уравнение, находим:

,

или

, где .

Заметим, что в общее решение входят полученные ранее решения .