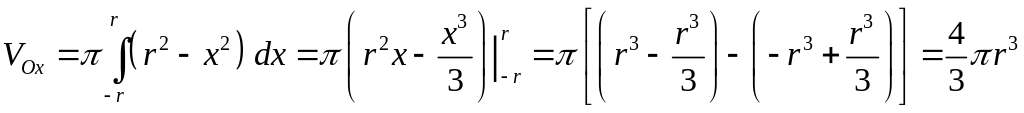- •Высшая математика
- •Введение
- •Глава I. Неопределенные и определенные интегралы
- •1.Неопределенный интеграл
- •Непосредственное интегрирование.
- •Интегралы вида .
- •Интегралы вида
- •Основные методы вычисления определенных интегралов
- •Формула Ньютона – Лейбница.
- •2.Замена переменной в определенном интеграле.
- •Интегрирование по частям в определенном интеграле.
- •3. Несобственные интегралы
- •4. Приложения определенных интегралов
- •Глава 2. Дифференциальные уравнения
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Дифференциальные уравнения первого порядка Дифференциальные уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка. Уравнение Бернулли
- •3. Дифференциальные уравнения, допускающие понижение порядка Уравнение вида .
- •Уравнение вида .
- •4. Линейные дифференциальные уравнения - го порядка.
- •5. Системы дифференциальных уравнений
- •Глава 3. Дифференциальное исчисление функций многих переменных
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Предел и непрерывность функции
- •Частные производные. Дифференциал функции
- •Производная в данном направлении. Градиент
- •Экстремумы функции нескольких переменных
- •Оглавление
- •Глава I. Неопределенные и определенные интегралы………….…3
- •3. Несобственные интегралы ……………………………………………….15
- •4. Приложения определенных интегралов ………………………………...17
- •Глава II. Дифференциальные уравнения ……………………………...18
- •Глава III. Дифференциальное исчисление функций многих переменных ……………………………………………………………………31
4. Приложения определенных интегралов
Площадь плоской фигуры
Пусть плоская
фигура ограничена кривыми
![]() и
и
![]() ,
при условии, что функции
,
при условии, что функции
![]() - непрерывны и
- непрерывны и
![]() ,
и вертикальными прямыми
,
и вертикальными прямыми
![]() и
.
Тогда площадь
данной
фигуры
вычисляется по формуле:
и
.
Тогда площадь
данной
фигуры
вычисляется по формуле:
![]() .
(16)
.
(16)
Если фигура
ограничена кривой, которая задана
параметрическими уравнениями
![]() ,
,
![]() ,
прямыми
,
прямыми
![]() и осью
и осью
![]() ,
то площадь данной фигуры вычисляется
по формуле:
,
то площадь данной фигуры вычисляется
по формуле:
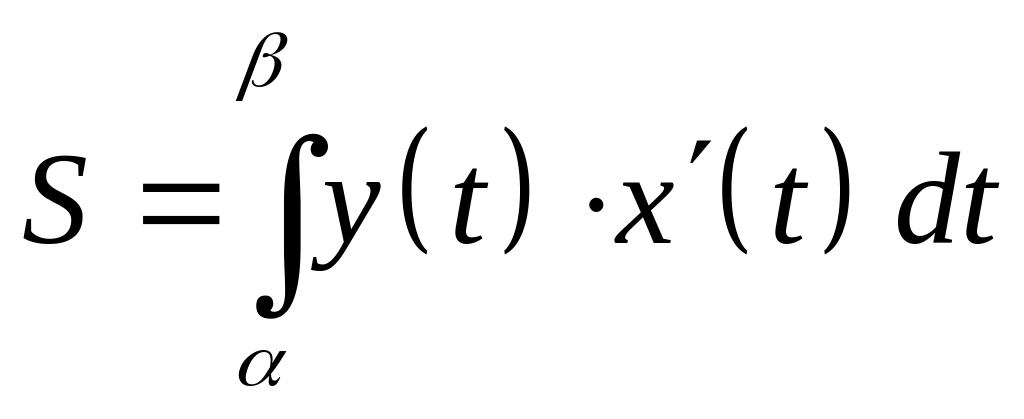 ,
(17)
,
(17)
где
![]() .
.
Если фигура
ограничена кривой, которая задана
уравнением в полярных координатах
![]() ,
и двумя лучами
,
и двумя лучами
![]() ,
то площадь
данной фигуры вычисляется по формуле:
,
то площадь
данной фигуры вычисляется по формуле:
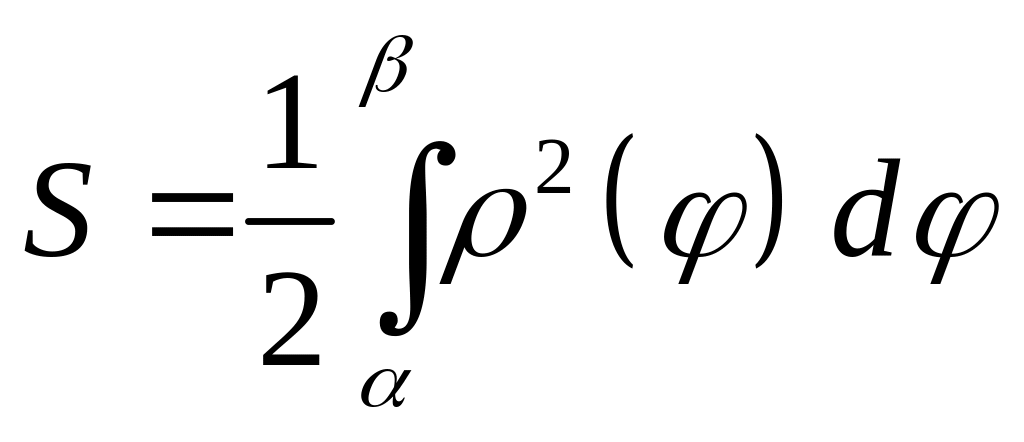 .
(18)
.
(18)
Длина дуги кривой
Если гладкая кривая
задана уравнением
,
то длина её дуги от точки
![]() до точки
до точки
![]() вычисляется по формуле:
вычисляется по формуле:
![]() .
(19)
.
(19)
Если гладкая кривая
задана параметрическими уравнениями
![]() ,
то
,
то
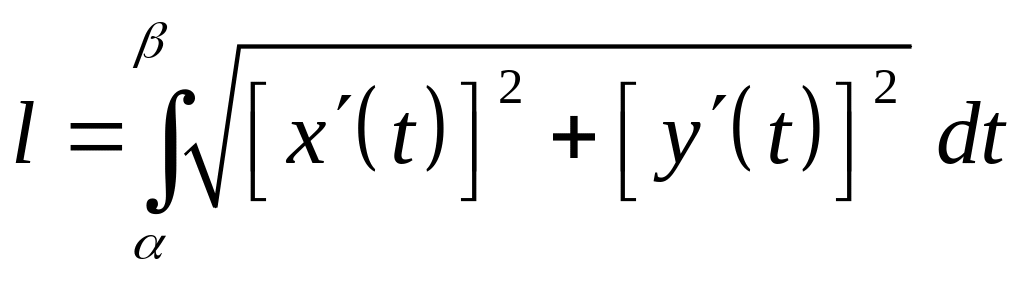 .
(20)
.
(20)
Если задана гладкая
пространственная кривая параметрическими
уравнениями
![]() ,
то справедлива формула аналогичная
(20):
,
то справедлива формула аналогичная
(20):
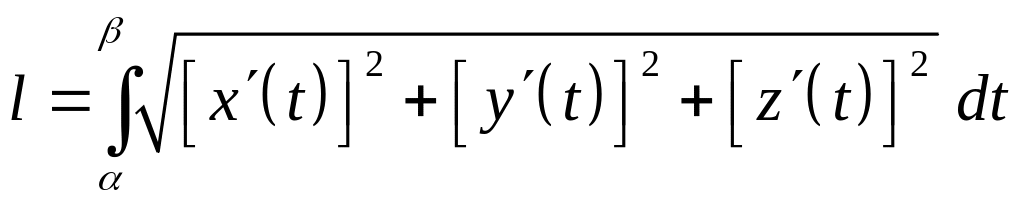 .
(21)
.
(21)
Если гладкая кривая
задана уравнением в полярных координатах
![]() ,
то
,
то
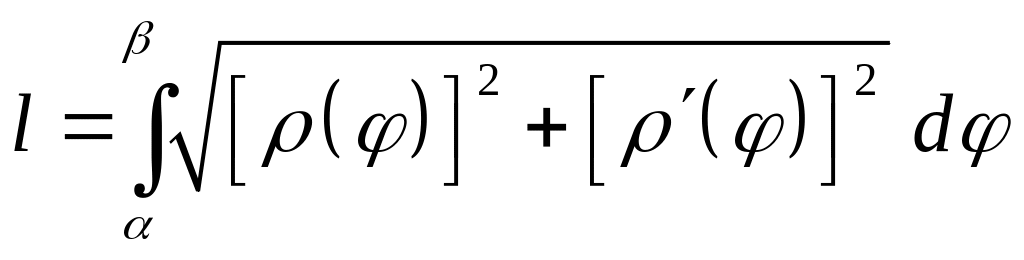 .
(22)
.
(22)
Площадь поверхности вращения
Площадь поверхности,
образованной вращением дуги кривой
![]() ,
,
![]() вокруг оси
,
вычисляется по формуле:
вокруг оси
,
вычисляется по формуле:
![]() .
(23)
.
(23)
Если кривая задается
параметрическими уравнениями
,
![]() ,
то:
,
то:
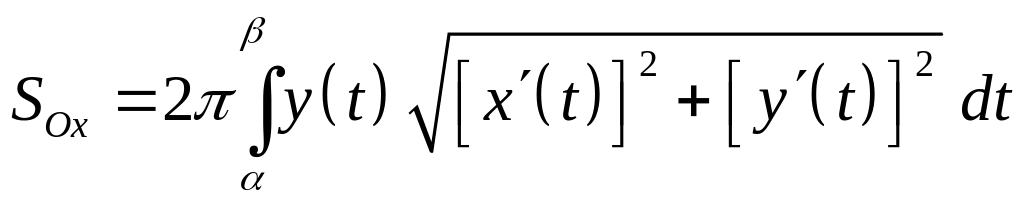 .
(24)
.
(24)
Объём тела
Если площадь
![]() сечения тела плоскостью, перпендикулярной
оси
,
является непрерывной функцией на отрезке
,
то объём тела вычисляется по формуле:
сечения тела плоскостью, перпендикулярной
оси
,
является непрерывной функцией на отрезке
,
то объём тела вычисляется по формуле:
![]() .
(25)
.
(25)
Объем тела,
образованного
вращением вокруг оси
фигуры, ограниченной кривыми
![]() ,
,
![]() (
(![]() )
и прямыми
,
вычисляется по формуле:
)
и прямыми
,
вычисляется по формуле:
![]() .
(26)
.
(26)
Задание 1.
Вычислить
площадь фигуры, ограниченной линиями
![]() и
и
![]() .
Сделать чертеж.
.
Сделать чертеж.
Решение. Найдем точки пересечения кривых:
![]() ,
,
откуда
![]() .
Тогда по формуле вычисления площади
плоской фигуры (16) имеем:
.
Тогда по формуле вычисления площади
плоской фигуры (16) имеем:
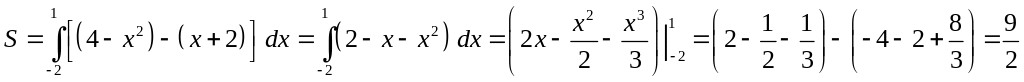
Сделаем чертеж.
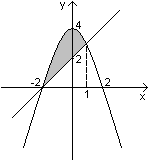
Задание 2.
Вычислить
длину дуги окружности
![]() .
.
Решение.
Кривая задана в параметрическом виде,
следовательно, вычислим длину дуги по
формуле (20). Имеем:
![]() и тогда
и тогда
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Задание 3.
Вычислить
площадь поверхности сферы, образованной
вращением окружности
![]() вокруг оси
.
вокруг оси
.
Решение.
Разрешим уравнение окружности относительно
![]() .
Пусть для определенности
.
Пусть для определенности
![]() .
Имеем:
.
Имеем:
![]() ;
;
![]() ;
;
![]() .
.
Тогда
![]() .
.
Задание 4.
Вычислить
объем шара,
образованного вращением вокруг оси
фигуры, ограниченной окружностью
![]() .
.
Решение.
Из уравнения окружности имеем:
![]() .
Воспользуемся теперь формулой (26),
положив
.
Воспользуемся теперь формулой (26),
положив
![]() ,
,
![]() .
Тогда получим:
.
Тогда получим: