Основные методы вычисления определенных интегралов
Формула Ньютона – Лейбница.
Если - первообразная непрерывной функции на отрезке , то справедлива формула Ньютона – Лейбница:
.
(7)
2.Замена переменной в определенном интеграле.
Пусть требуется
вычислить интеграл
,
где функция
непрерывна на отрезке
.
Полагая
,
где
непрерывно дифференцируемая функция
на отрезке
,
причем
,
получим:
.
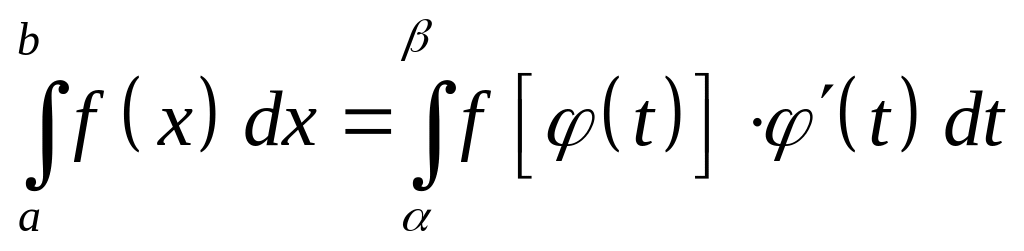(8)
Интегрирование по частям в определенном интеграле.
Если и - непрерывно дифференцируемые функции на отрезке , то справедлива формула интегрирования по частям:
.
(9)
Задание 1.
Вычислить
интеграл:
.
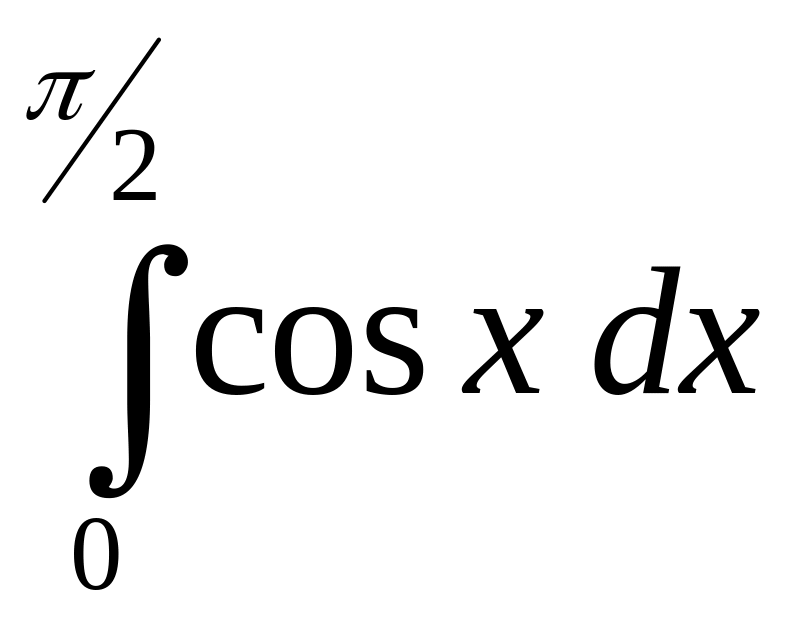Решение.
Так как первообразной подынтегральной
функции
является функция
,
то по формуле Ньютона-Лейбница получаем:
.
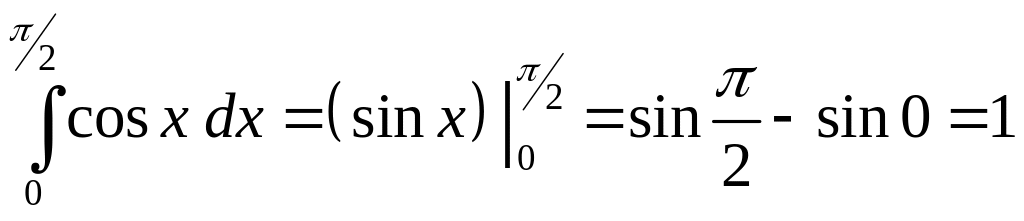Задание 2.
Вычислить интеграл:
.
Решение.
Сделаем в данном интеграле замену
переменной. Положим
,
тогда
.
Найдем новые пределы интегрирования:
если
,
то
и, следовательно,
;
если
,
то
,
и, следовательно,
.
Тогда имеем:
.
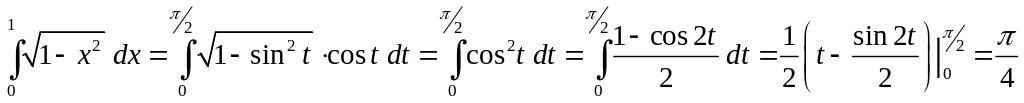Задание 3.
Вычислить
интеграл:
.
Решение.
Воспользуемся формулой интегрирования
по частям в определенном интеграле (9).
Положим:
.
Тогда
.
Следовательно,
.
3. Несобственные интегралы
Несобственные интегралы по бесконечному промежутку
Пусть функция
непрерывна на промежутке
.
Несобственным
интегралом от функции
по промежутку
называют предел интеграла
при
и обозначают
.
Следовательно, по определению:
.
(10)
Если предел в правой части равенства (10) существует и конечен, то говорят, что несобственный интеграл сходится, в противном случае говорят, что несобственный интеграл расходится.
Аналогично определяются несобственные интегралы и для других бесконечных промежутков:
(11)
и
.
(12)
Заметим, что
несобственный интеграл от функции
по промежутку
сходится, если сходятся оба несобственных
интеграла стоящих в правой части
равенства (12), т.е. существуют оба предела.
Несобственные интегралы от неограниченных функций
Пусть функция
непрерывна на отрезке
,
а при
функция обращается в бесконечность:
.
Несобственным интегралом
от функции
на отрезке
в данном случае называют предел интеграла
при
и обозначают
.
Следовательно, по определению имеем:
.
(13)
Если предел в правой части равенства (13) существует и конечен, то говорят, что несобственный интеграл сходится, в противном случае говорят, что несобственный интеграл расходится.
Аналогично определяются несобственные интегралы от функции на отрезке в других случаях:
1) в случае
:
.
(14)
2) в случае
,
где
:
.
(15)
Заметим, что несобственный интеграл от функции на отрезке в случае , где , сходится, если сходятся оба несобственных интеграла правой части равенства (15), т.е. существуют оба предела.
Задание 1.
Вычислить несобственный интеграл или
установить его расходимость:
.
Решение.
Данный интеграл является несобственным
по бесконечному промежутку
.
По определению имеем:
.
Следовательно, данный несобственный интеграл сходится и равен 1.
Задание 2.
Вычислить
несобственный интеграл или установить
его расходимость:
.
Решение.
Данный интеграл является несобственным
интегралом от функции
на отрезке
в случае
.
По определению имеем:
.
Следовательно, данный несобственный интеграл расходится.