
- •Высшая математика
- •Введение
- •Глава I. Неопределенные и определенные интегралы
- •1.Неопределенный интеграл
- •Непосредственное интегрирование.
- •Интегралы вида .
- •Интегралы вида
- •Основные методы вычисления определенных интегралов
- •Формула Ньютона – Лейбница.
- •2.Замена переменной в определенном интеграле.
- •Интегрирование по частям в определенном интеграле.
- •3. Несобственные интегралы
- •4. Приложения определенных интегралов
- •Глава 2. Дифференциальные уравнения
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Дифференциальные уравнения первого порядка Дифференциальные уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка. Уравнение Бернулли
- •3. Дифференциальные уравнения, допускающие понижение порядка Уравнение вида .
- •Уравнение вида .
- •4. Линейные дифференциальные уравнения - го порядка.
- •5. Системы дифференциальных уравнений
- •Глава 3. Дифференциальное исчисление функций многих переменных
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Предел и непрерывность функции
- •Частные производные. Дифференциал функции
- •Производная в данном направлении. Градиент
- •Экстремумы функции нескольких переменных
- •Оглавление
- •Глава I. Неопределенные и определенные интегралы………….…3
- •3. Несобственные интегралы ……………………………………………….15
- •4. Приложения определенных интегралов ………………………………...17
- •Глава II. Дифференциальные уравнения ……………………………...18
- •Глава III. Дифференциальное исчисление функций многих переменных ……………………………………………………………………31
Интегралы вида
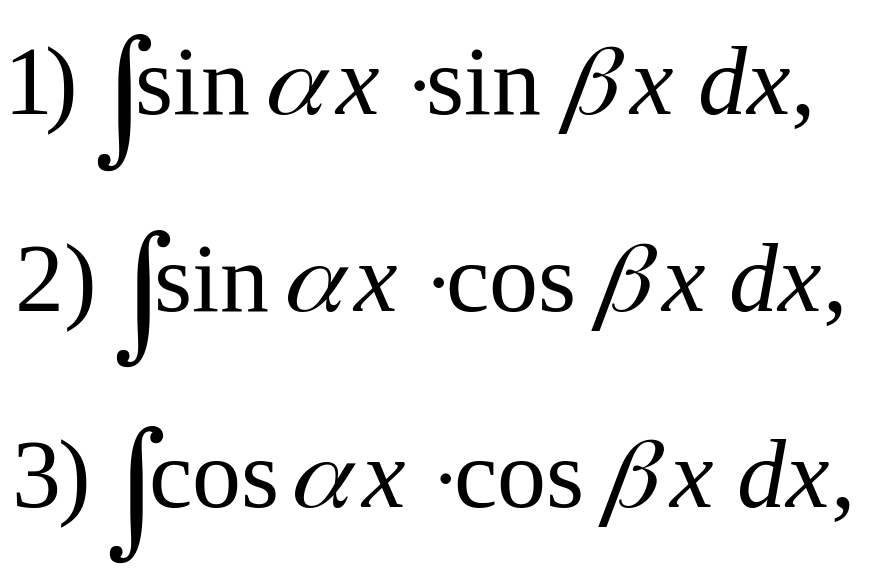
где![]() Для
вычисления данных интегралов применяются
тригонометрические формулы:
Для
вычисления данных интегралов применяются
тригонометрические формулы:
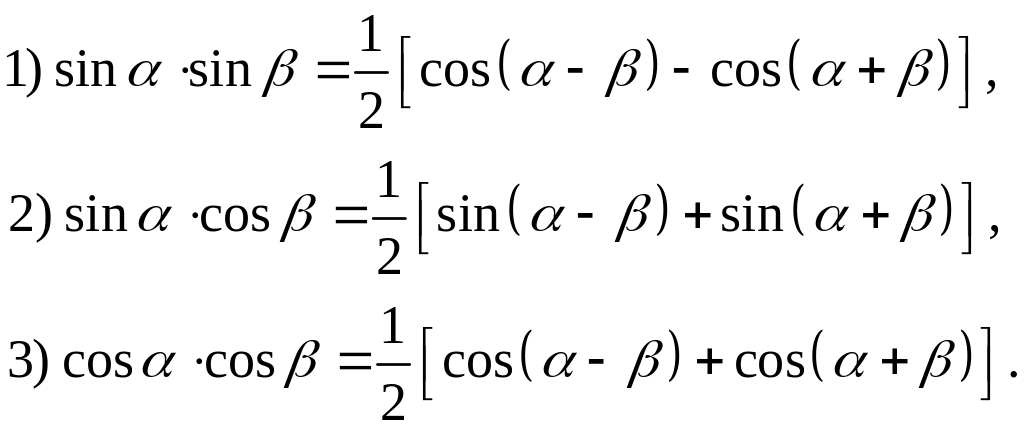
Интегрирование иррациональных функций
Рассмотрим интеграл вида
 ,
где
,
где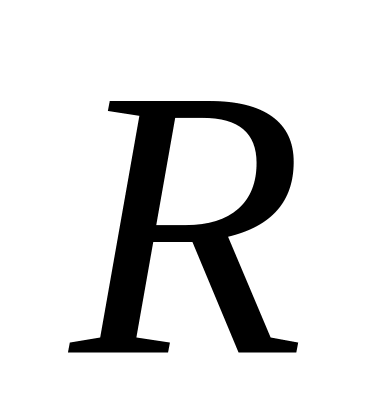 -рациональная
функция своих аргументов;
-рациональная
функция своих аргументов;
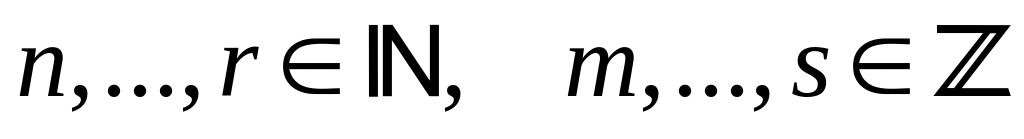 .
.
Замена
![]() ,
где
,
где
![]() ,
(
,
(![]() -
наименьшее общее кратное), приводит
данный интеграл к интегралу от рациональной
функции нового аргумента
.
-
наименьшее общее кратное), приводит
данный интеграл к интегралу от рациональной
функции нового аргумента
.
Рассмотрим интеграл вида
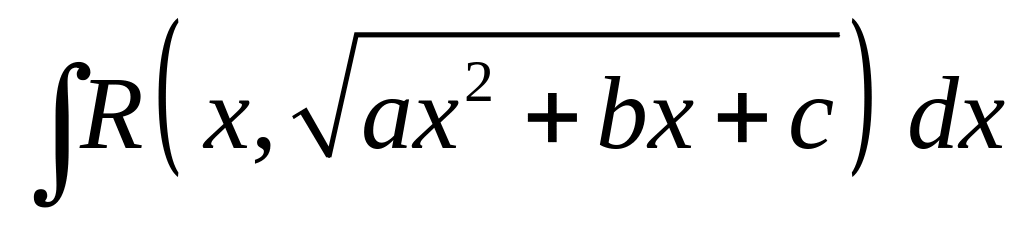 .
Для вычисления данного интеграла в
квадратичном трехчлене выделяют полный
квадрат:
.
Для вычисления данного интеграла в
квадратичном трехчлене выделяют полный
квадрат:
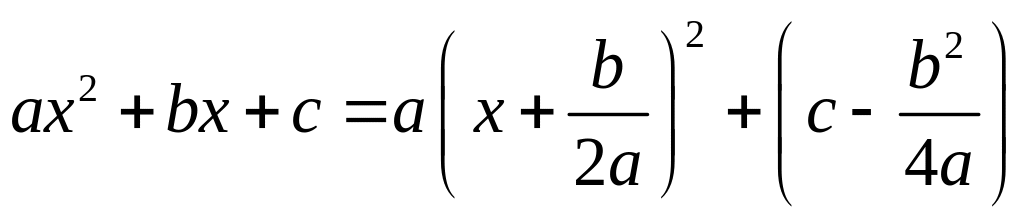 .
Далее заменой
.
Далее заменой
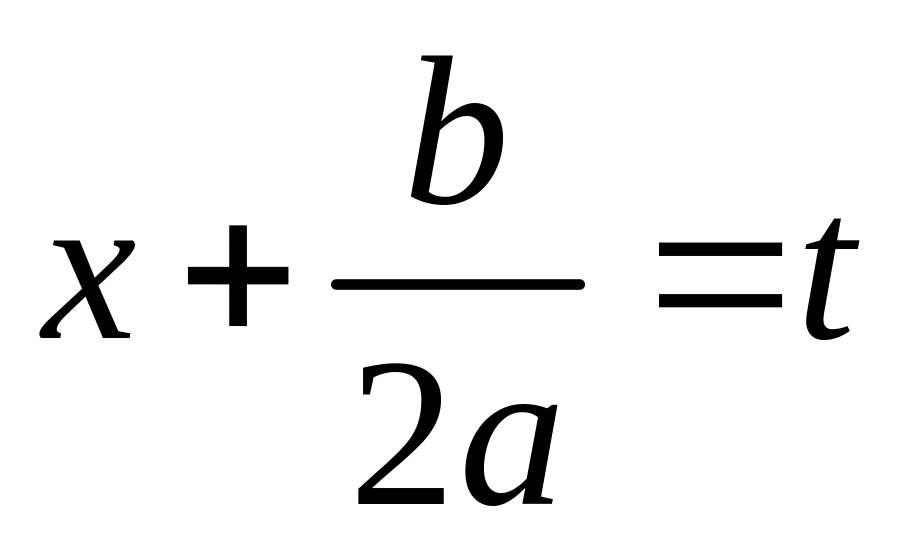 исходный интеграл приводится к одному
из следующих интегралов:
исходный интеграл приводится к одному
из следующих интегралов:
![]() ,
если
,
если
![]() где
где
![]()
![]() ,
если
,
если
![]() где
где
![]()
![]() ,
если
,
если
![]() где
где
![]()
Последние интегралы с помощью соответствующих подстановок:
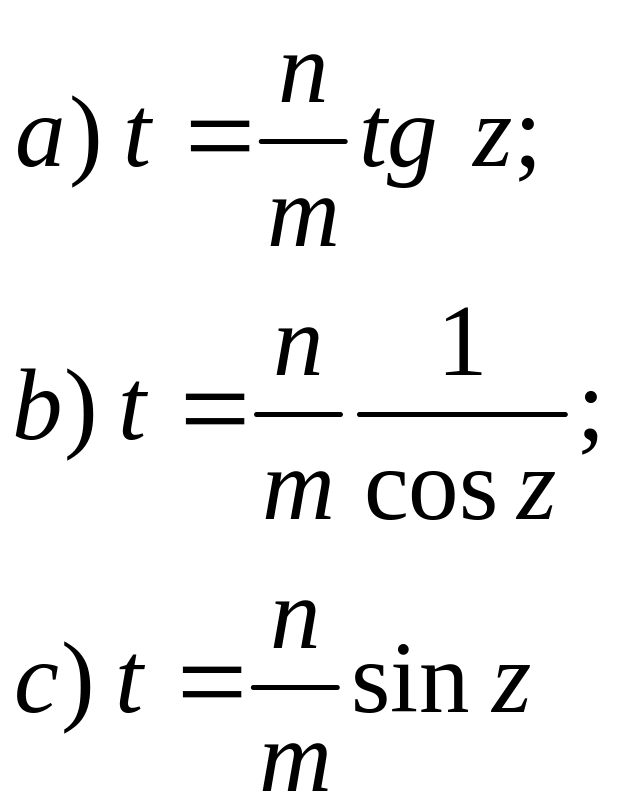
приводятся к интегралам вида .
Задание 1.
Вычислить
интеграл:
![]() .
.
Решение. Данный интеграл можно вычислить непосредственным интегрированием. Действительно,
![]() .
.
Задание 2.
Вычислить интеграл:
![]() .
.
Решение.
Данный интеграл не является табличным.
Его можно вычислить методом замены
переменной. Положим:
![]() Тогда
Тогда
![]() ,
т.е.
,
т.е.
![]() .
Следовательно,
.
Следовательно,
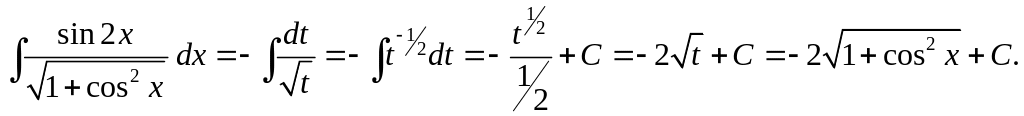
Задание 3.
Вычислить интеграл:![]() .
.
Решение.
Данный интеграл не является табличным.
Методом замены переменной мы также не
достигнем нужного нам результата. Его
можно вычислить методом интегрирования
по частям. Для этого положим
![]() .
Тогда
.
Тогда
![]() .
Следовательно, по
формуле
интегрирования по частям (2) имеем:
.
Следовательно, по
формуле
интегрирования по частям (2) имеем:
![]() .
.
Задание 4.
Найти интеграл:
![]() .
.
Решение.
Заметим, что подынтегральная функция
![]() данного интеграла является правильной
рациональной функцией. Разложим её на
сумму простейших дробей:
данного интеграла является правильной
рациональной функцией. Разложим её на
сумму простейших дробей:
![]() ,
(3)
,
(3)
где
![]() -
неопределенные коэффициенты.
-
неопределенные коэффициенты.
Д![]() ля
нахождения значений коэффициентов
правую часть равенства (3) приводим к
общему знаменателю:
ля
нахождения значений коэффициентов
правую часть равенства (3) приводим к
общему знаменателю:
(4)
Из равенства дробей (3) и (4) получаем:
![]() .
.
Два многочлена равны, если равны коэффициенты при одинаковых степенях . Следовательно, имеем:
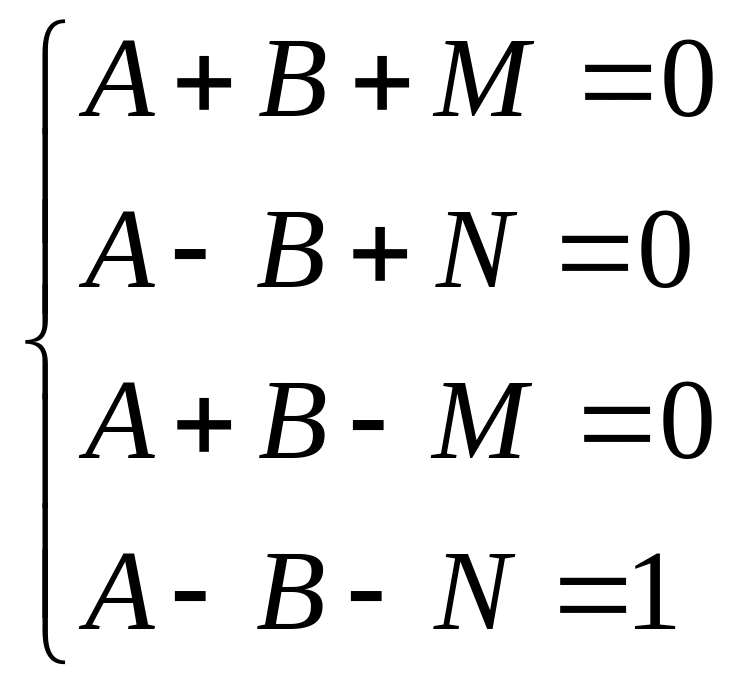 (5)
(5)
Решив систему алгебраических уравнений (5), получим:
![]() .
.
Таким образом, разложение дроби на сумму простейших дробей имеет вид:
![]() .
.
Следовательно, исходный интеграл равен:
![]()
![]() .
.
Задание 5.
Найти интеграл:
![]() .
.
Решение. Данный интеграл является интегралом от рациональной функции аргументов и . Полагая , имеем
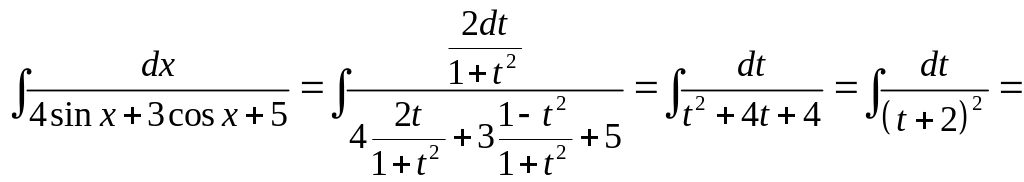
![]()
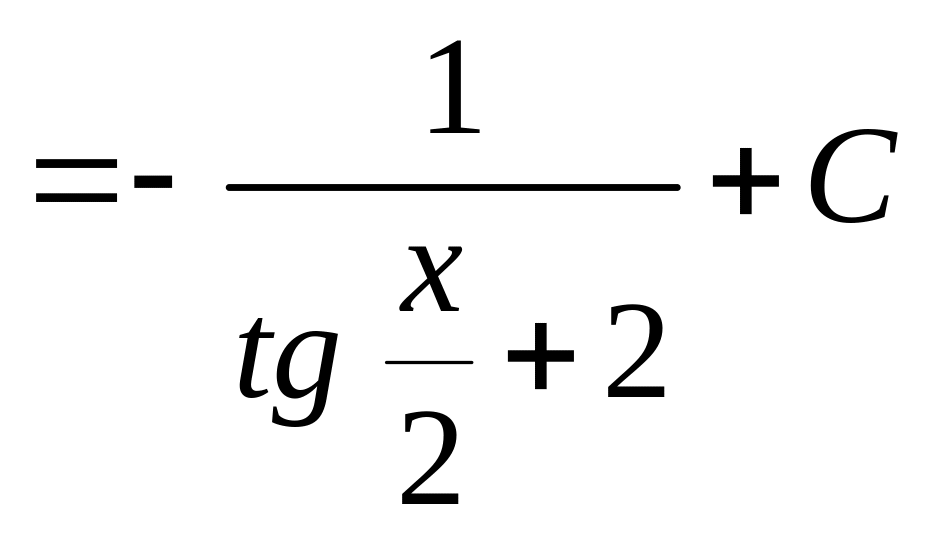 .
.
Задание 6.
Найти интеграл:
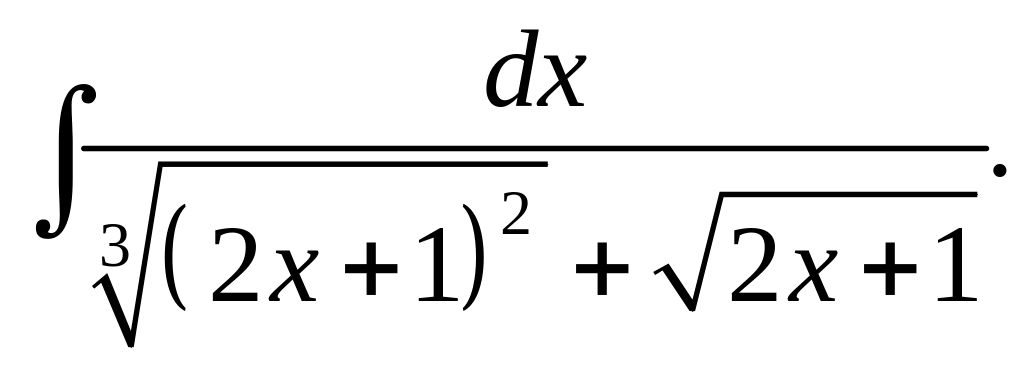
Решение.
Рассматриваемый интеграл является
интегралом от иррациональной функции.
Подстановка
![]() приведёт данный интеграл к интегралу
от рациональной функции аргумента
.
Действительно имеем:
приведёт данный интеграл к интегралу
от рациональной функции аргумента
.
Действительно имеем:
![]() и
и
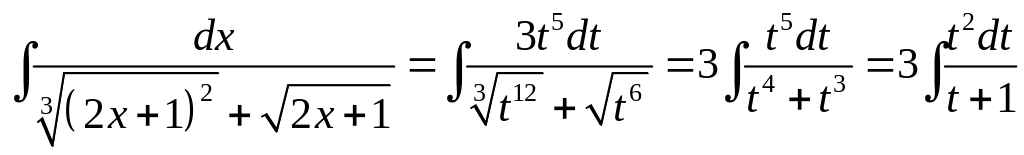 .
.
Подынтегральная
функция
![]() полученного интеграла является
неправильной рациональной функцией.
Чтобы вычислить интеграл, необходимо
выделить целую часть дроби
и представить эту дробь в виде суммы
многочлена и правильной рациональной
функции (выполнив деление многочленов).
В результате получим:
полученного интеграла является
неправильной рациональной функцией.
Чтобы вычислить интеграл, необходимо
выделить целую часть дроби
и представить эту дробь в виде суммы
многочлена и правильной рациональной
функции (выполнив деление многочленов).
В результате получим:
![]() .
.
Следовательно, имеем:
![]() .
.
Таким образом,
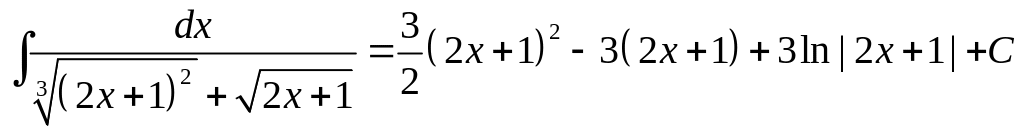 .
.
2. Определенный интеграл
Определение определенного интеграла
Пусть функция
![]() определена на отрезке
определена на отрезке
![]() .
Разобьем отрезок
произвольным образом на
частей (элементарных
отрезков):
.
Разобьем отрезок
произвольным образом на
частей (элементарных
отрезков):
![]() .
.
Составим сумму
![]() ,
где
,
где
![]() (точки
пунктуации),
(точки
пунктуации),
![]() (длины
элементарных отрезков),
(длины
элементарных отрезков),
![]() .
Эта сумма называется интегральной
суммой Римана.
Обозначим
.
Эта сумма называется интегральной
суммой Римана.
Обозначим
![]() .
.
Если существует
предел интегральной суммы Римана при
условии, что
![]() ,
причем этот предел не зависит ни от
способа разбиения отрезка
на элементарные отрезки, ни от способа
выбора точек пунктуации
,
причем этот предел не зависит ни от
способа разбиения отрезка
на элементарные отрезки, ни от способа
выбора точек пунктуации
![]() ,
то функция
называется интегрируемой
на отрезке
,
а сам предел называется определенным
интегралом от
функции
на отрезке
и обозначается
,
то функция
называется интегрируемой
на отрезке
,
а сам предел называется определенным
интегралом от
функции
на отрезке
и обозначается
![]() .
Следовательно, по определению имеем:
.
Следовательно, по определению имеем:
![]() .
(6)
.
(6)
Основные свойства определенного интеграла
1)
![]() ,
где
,
где
![]()
2)
![]()
3)
![]()
4)
![]()
