5. Системы дифференциальных уравнений

Рассмотрим линейную систему с постоянными коэффициентами второго порядка:

(33)

Здесь - постоянные числа, - неизвестные функции.

Решением системы (33) называется совокупность непрерывно дифференцируемых функций , обращающих уравнения системы (33) в тождества.

Общим решением системы (33) называется совокупность непрерывно дифференцируемых функций , где - произвольные постоянные, удовлетворяющих двум условиям:

1. при любых значениях постоянных и 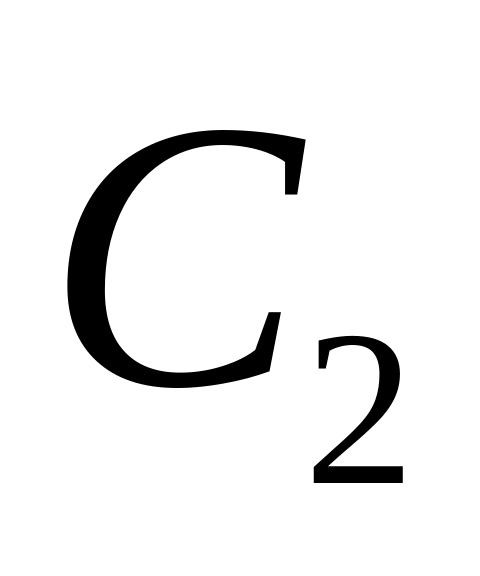функции 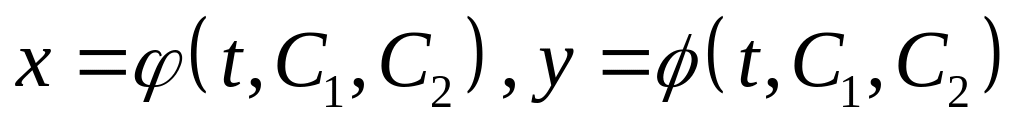являются решениями системы (33);

2. любое решение системы (33) может быть получено из функций при соответствующих значениях постоянных и .

Рассмотрим один из методов решения систем дифференциальных уравнений – метод исключения.

Продифференцируем одно из уравнений системы (33) по (например, первое уравнение). Получим:

. (34)

Подставим в уравнение (34) значение из второго уравнения системы (33): (35)

Далее, из первого уравнения системы (33) находим значение

. (36)

и подставим его в уравнение (35). В результате получим уравнение:

. (37)

Уравнение (37) - линейное однородное уравнение 2-го порядка с постоянными коэффициентами с одной неизвестной функцией . Методы интегрирования ЛОДУ рассмотрены в предыдущем пункте. Пусть общее решение ЛОДУ (37) имеет вид:

(38)

где - произвольные постоянные.

Подставляя функции и в формулу (36), находим вторую искомую функцию:

. (39)

Совокупность формул (38) и (39) дает общее решение системы (33):

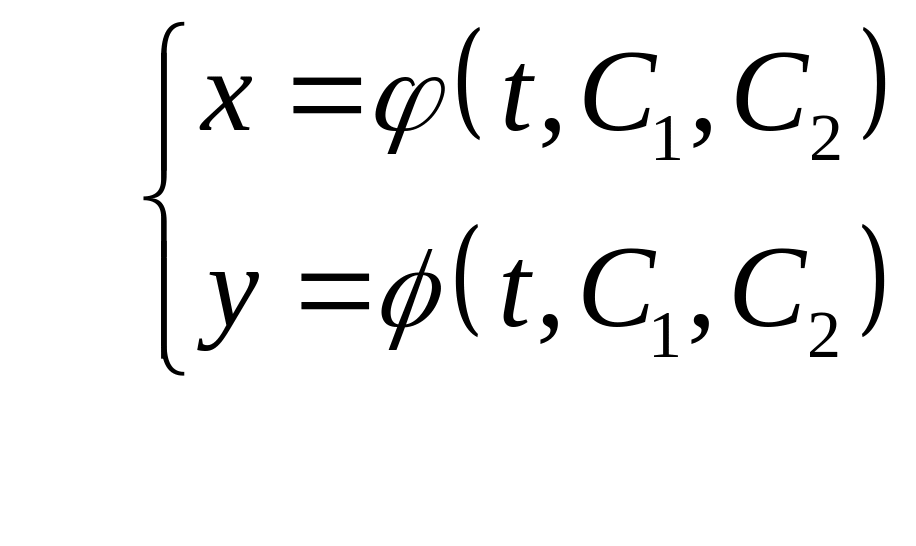
Задание. Решить систему:

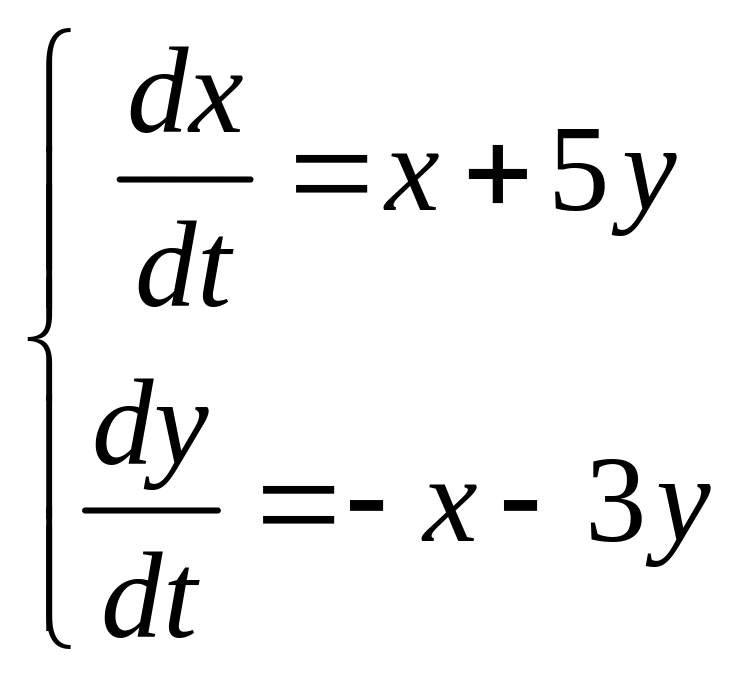
Решение. Для данной системы . Следовательно, чтобы найти функцию , надо решить уравнение (см. (37)):

. (40)

Характеристическое уравнение для ЛОДУ (40) имеет вид:

Его корни . Следовательно, общее решение уравнения (40) имеет вид:

. (41)

Далее, чтобы найти функцию воспользуемся выражением (36). Имеем:

. (42)

Совокупность формул (41) и (42) дает общее решение исходной системы: