3.10. Математическое описание процессов электромеханического

преобразования энергии в асинхронном двигателе

Схема включения трехфазного асинхронного двигателя с фазным ротором показана на рис. 3.26, а, соответствующая ей двухфазная модель представлена на рис. 3.26, б. Мате­матическое описание процессов электромеханического преоб­разования энергии наиболее удобно получить в синхрон­ных осях х, у, при этом, как было показано в гл. 2, синусоидально изменяющиеся реальные переменные машины преобразуются в постоянные величины, характеризующие про­екции изображающего вектора на синхронно с ним вращаю­щиеся координатные оси х и у. Наиболее компактной за­писью уравнений механической характеристики является ком­плексная форма. В осях х, у эти уравнения мож­но получить с помощью (2.27), положив:

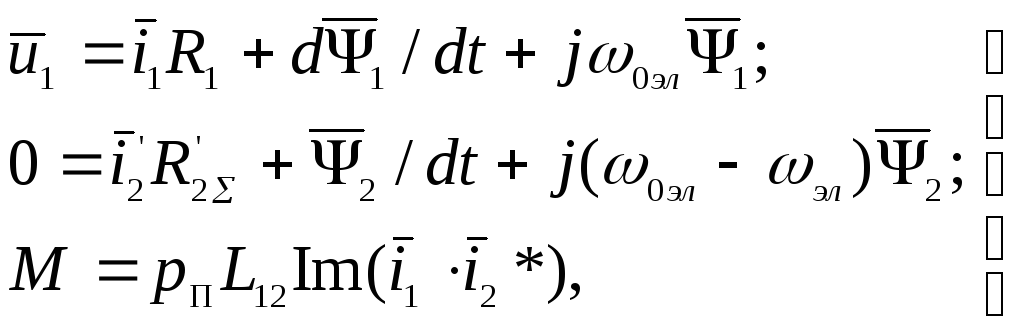(3.64)

где — суммарное активное сопротивление фа­зы двигателя.

Уравнения потокосцеплений:

(3.65)

С помощью (3.65) можно выразить токи через потокосцепления:

; (3.66)

. (3.67)

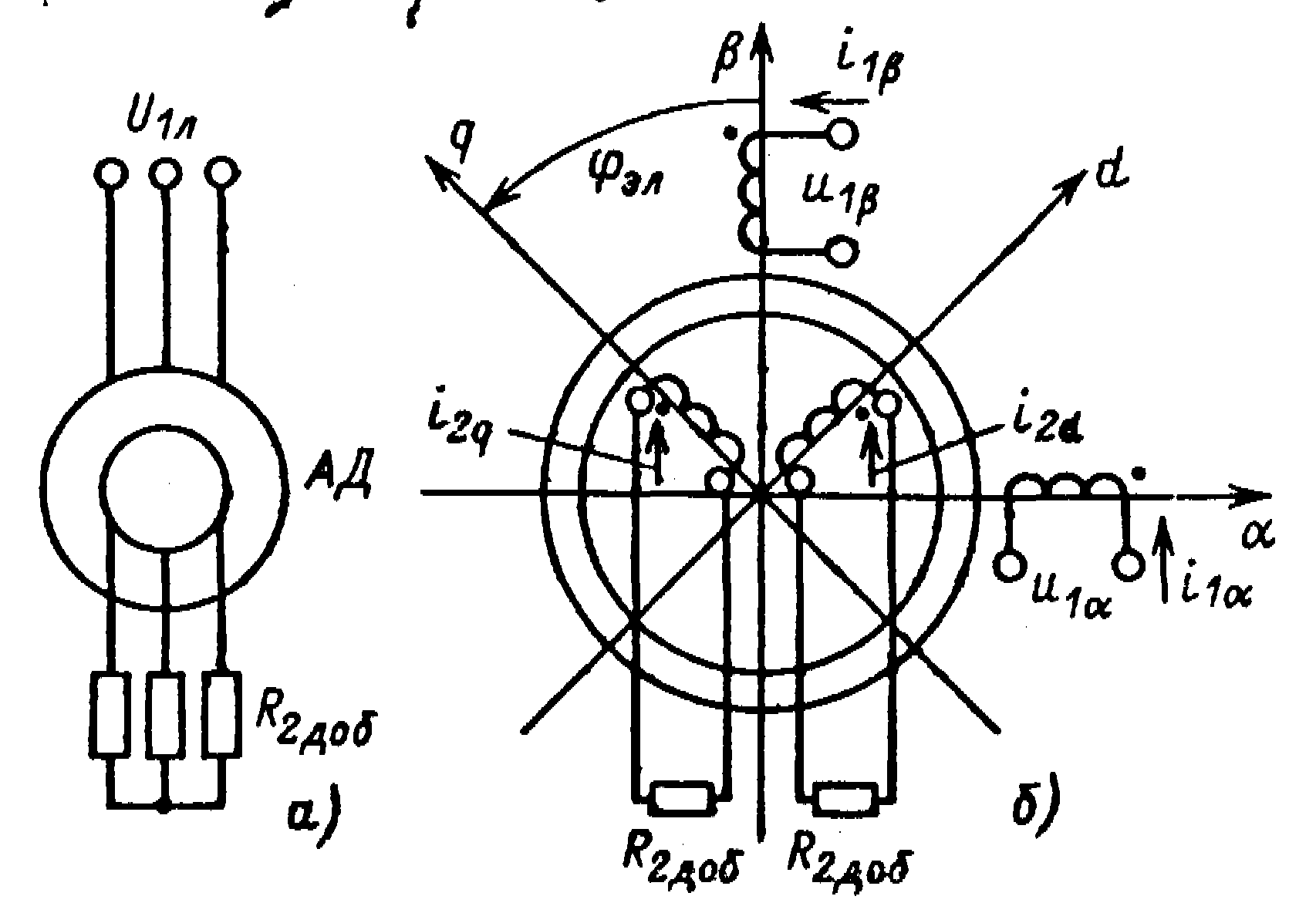
Рис. 3.26. Схемы трехфазного асинхронного двигателя (а) и его двухфазной модели (б)

Подставив (3.66) и (3.67) в (3.64), можно получить урав­нения механической характеристики, выраженные через потокосцепления:

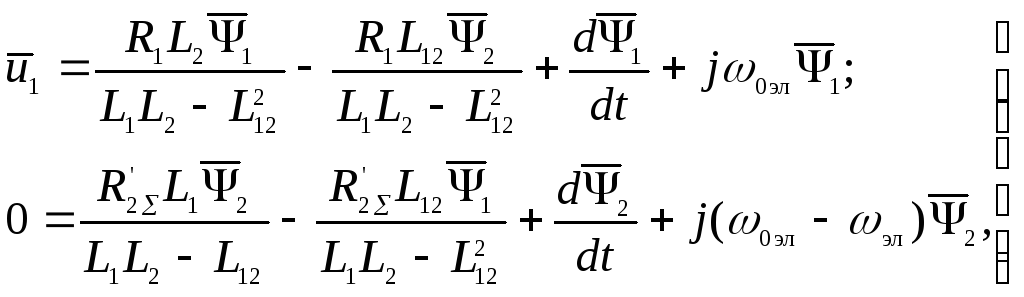
(3.68)

Уравнения (3.64) и (3.68) используются в дальнейшем для анализа динамических свойств асинхронного электроме­ханического преобразователя. Для анализа статических режи­мов преобразования энергии используем выражение намаг­ничивающего тока машины

. (3.69)

С учетом (3.69) уравнения потокосцеплений (3.65) могут быть представлены в виде

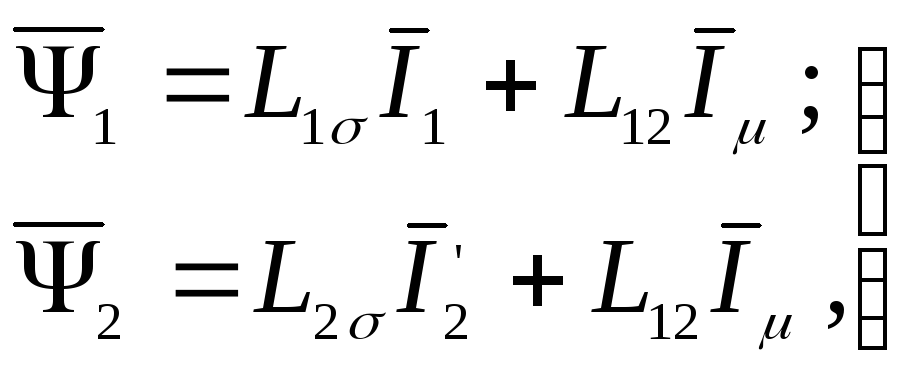(3.70)

где — индуктивности рассеяния статорной и роторной обмоток.

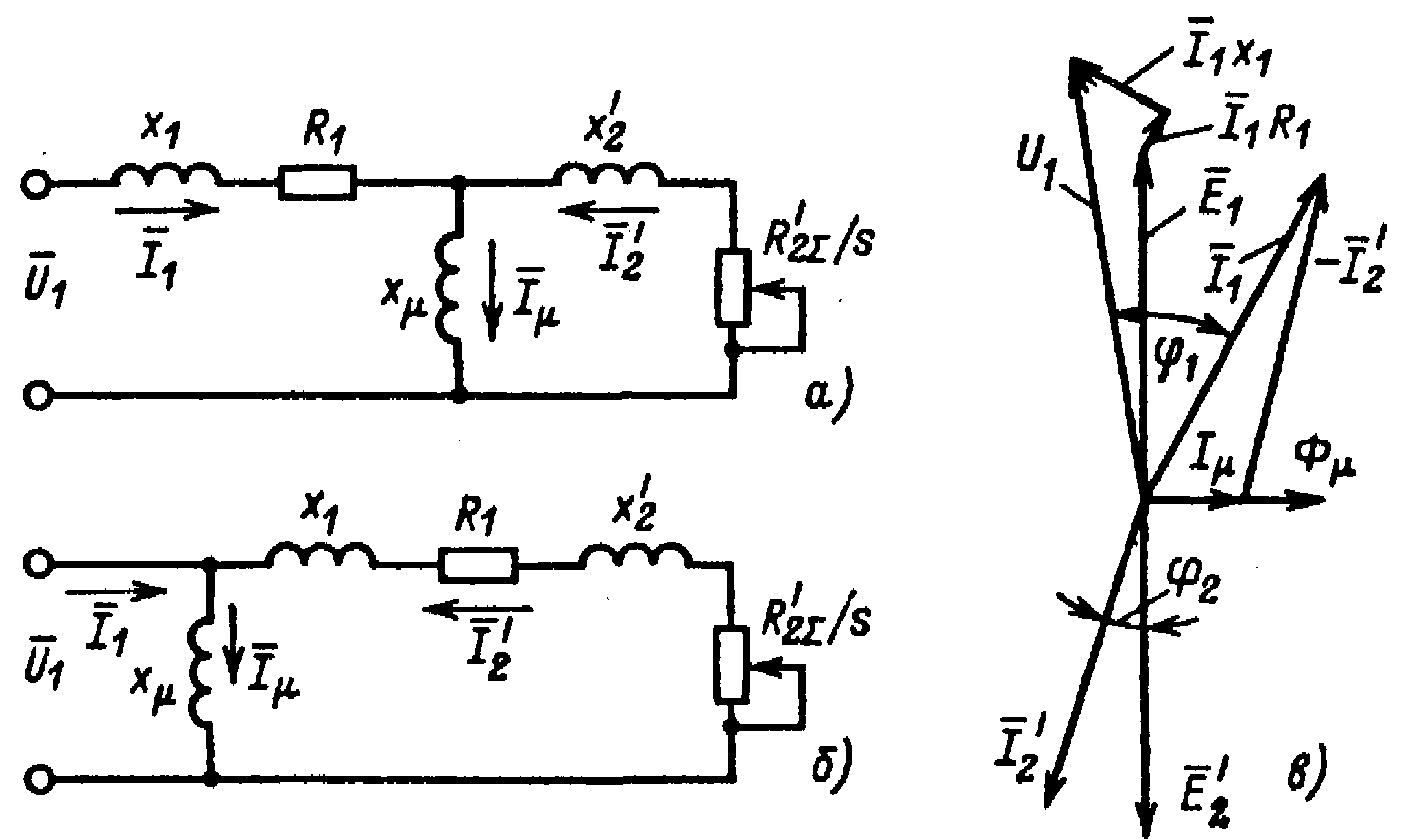
Рис. 3.27. Схемы замещения фазы (а,б) и векторная диаграмма (в) асинхронного двигателя

Приняв для статического режима в (3.64) , запишем первые два уравнения этой системы так:

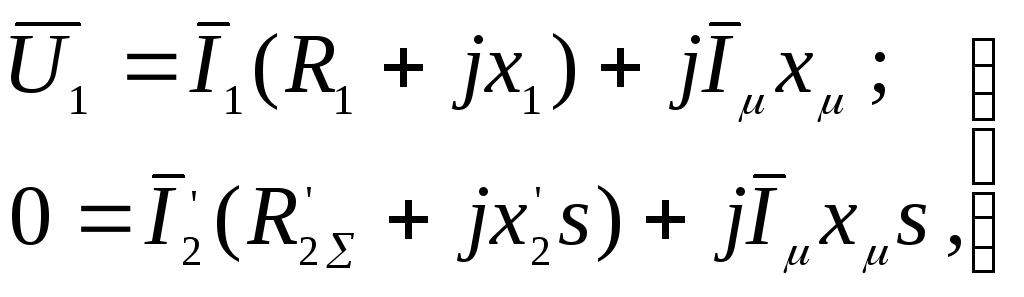(3.71)

где .

В уравнениях (3.71) величина представляет собой ЭДС фазы двигателя

,

поэтому их можно записать так:

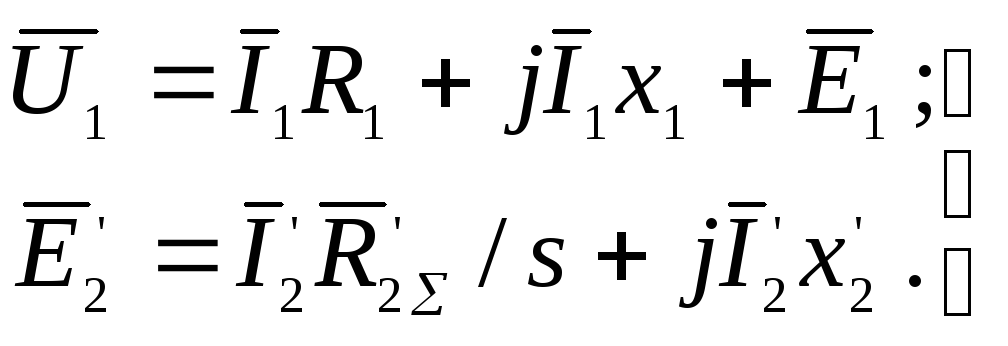(3.72)

Уравнения (3.72) записаны для двухфазной модели дви­гателя. Как было показано в § 2.4, переменные двухфаз­ной модели пропорциональны переменным реального дви­гателя, поэтому они являются также уравнениями электри­ческого равновесия в комплексной форме, записанными для любой фазы реального асинхронного двигателя при его ра­боте в статическом режиме. Им соответствуют схемы за­мещения фазы и векторная диаграмма, представленные на рис. 3.27.

Таким образом, математический аппарат обобщенной ма­шины позволяет достаточно просто, как частный случай по­лучить традиционные уравнения электрического равновесия, схему замещения и векторную диаграмму для статических режимов работы, известные из курса электрических машин.

Без большой погрешности намагничивающую ветвь схемы рис. 3.27, аможно вынести на выводы напряжения сети; соответствующая этому допущению схема замещения фазы асинхронного двигателя представлена на рис. 3.27,б. Ошибка, вносимая этим допущением, невелика потому, что в схеме рис. 3.27,бне учитывается лишь влияние падения напря­жения на сопротивлениях обмотки статора от намагничи­вающего тока на определяемый схемой ток ротора. Сле­дует иметь в виду, что эта схема не дает правильных пред­ставлений о зависимости намагничивающего тока от нагрузки двигателя, так как определяет неизменное значение этого тока .