
- •Введение
- •Общие сведения о метрических задачах. Методы преобразования комплексного чертежа как алгоритм решения задач
- •1.1. Метод замены плоскостей проекций. Четыре основные задачи на преобразование чертежа
- •1.2. Метод плоскопараллельного перемещения
- •1.2.1. Способ вращения вокруг проецирующей прямой
- •1.2.2. Способ вращения вокруг прямой уровня (способ совмещения)
- •1.3. Упражнения и задачи для самостоятельного решения
- •2. Задачи на определение расстояний
- •2.1. Определение расстояния от точки до другой точки
- •2.2. Определение расстояния от точки до прямой
- •2.3. Определение расстояния от точки до плоскости
- •2.4. Определение расстояния от точки до поверхности вращения
- •2.5. Определение расстояния между параллельными прямыми
- •2.6. Определение расстояния между скрещивающимися прямыми
- •2.7. Определение расстояния от прямой до параллельной ей плоскости
- •2.8. Определение расстояния от прямой до поверхности
- •2.9. Определение расстояния от плоскости до параллельной ей плоскости
- •2.10. Определение расстояния от плоскости до пересекающейся с ней поверхности
- •2.11. Упражнения и задачи для самостоятельного решения
- •3. Задачи на определение величины угла
- •3.1. Определение величины угла между пересекающимися прямыми
- •3.2. Определение величины угла между прямой общего положения и плоскостью общего положения
- •3.6. Упражнения и задачи для самостоятельного решения
- •644046, Г. Омск, пр. Маркса, 35
2.3. Определение расстояния от точки до плоскости
Расстояние от точки до плоскости можно определить одним из следующих способов:
1) прямым путем: опустить перпендикуляр из точки на плоскость, найти основание перпендикуляра и определить расстояние между точками – заданной и найденной;
2) вращением привести заданную систему в положение, когда плоскость перпендикулярна какой-либо плоскости проекций;
3) совмещением: провести через точку горизонтально или вертикальнопроецирующую плоскость, перпендикулярную к заданной плоскости, и совмещением вспомогательной плоскости с какой-либо плоскостью проекций найти положение заданной точки и линии пересечения плоскостей;
4) заменой плоскостей проекций: заменить одну из плоскостей проекций новой, которая перпендикулярна заданной плоскости.
Задача 11. Определить расстояние от точки К до плоскости треугольника ABC (рис. 14) методом замены плоскостей проекций.
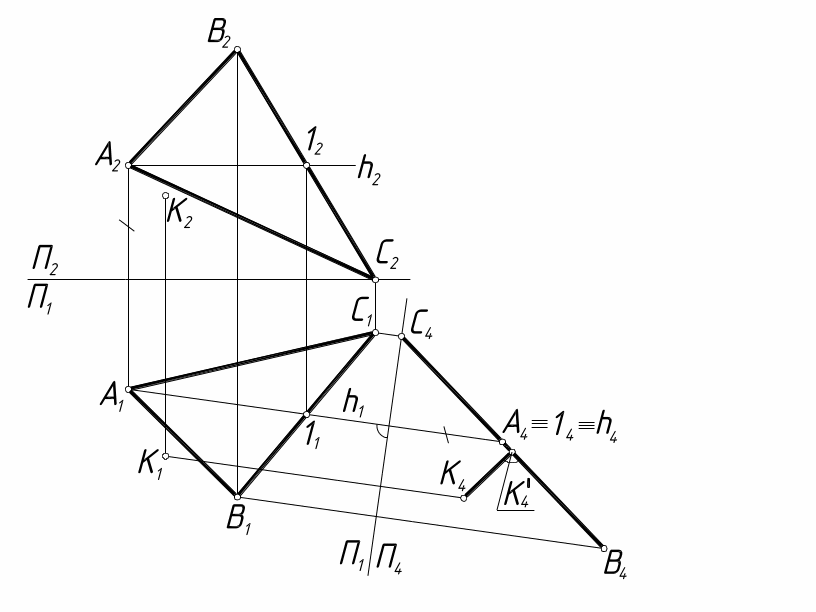
Рис. 14. Определение расстояния от точки до плоскости
Решение. Заменяем плоскость проекций П2 П4. Проводим горизонталь в плоскости треугольника. Новая ось проекций X1 h1. Находим проекции точки К4 и треугольника А4В4С4. Опускаем из точки К4 перпендикуляр на проекцию треугольника А4В4С4. Отрезок К4 К4' является искомым расстоянием.
2.4. Определение расстояния от точки до поверхности вращения
Расстояние от точки до поверхности вращения измеряется величиной отрезка нормали, проведенной из заданной точки. Основание нормали лежит на ближайшей точке меридиана, расположенного в одной плоскости с заданной точкой и осью вращения.
Задача 12. Найти расстояние от точки до поверхности вращения (рис. 15).

а б в
Рис. 15. Определение расстояния от точки до сферы
Решение. Если бы точка А находилась в одной плоскости с меридианом или экватором, тогда достаточно было бы соединить соответствующую проекцию с центром, чтобы определить искомое.
Решим эту задачу вращением вокруг фронтально проецирующей пря- мой – оси i, проходящей через центр сферы. Введем плоскость-посредник – фронтально Σ2 проецирующую плоскость через заданную точку А2 и ось i2. Плоскость Σ пересекает сферу по полуокружности, которая на плоскость П1 проецируется в полуэллипс. Повернем плоскость Σ2 вместе с точкой А2 вокруг оси до горизонта. Теперь сечение плоскостью Σ'2 спроецируется на П1 без искажения и совпадет с проекцией экватора, значит, новая проекция точки А'2 лежит в одной плоскости с экватором. Соединим А'1 с О1 и там, где этот отрезок пересечет экватор, обозначим точку М1.
Отрезок А'1М'1 измеряет расстояние от точки А' до преобразованного сечения сферы. Этот отрезок определяет расстояние от точки А до сферы, а точка М – ближайшая точка сферы к точке А.
2.5. Определение расстояния между параллельными прямыми
Расстояние между параллельными прямыми измеряется отрезком перпендикуляра между ними.
Задача 13. Найти расстояние между параллельными прямыми общего положения методом замены плоскостей проекций.
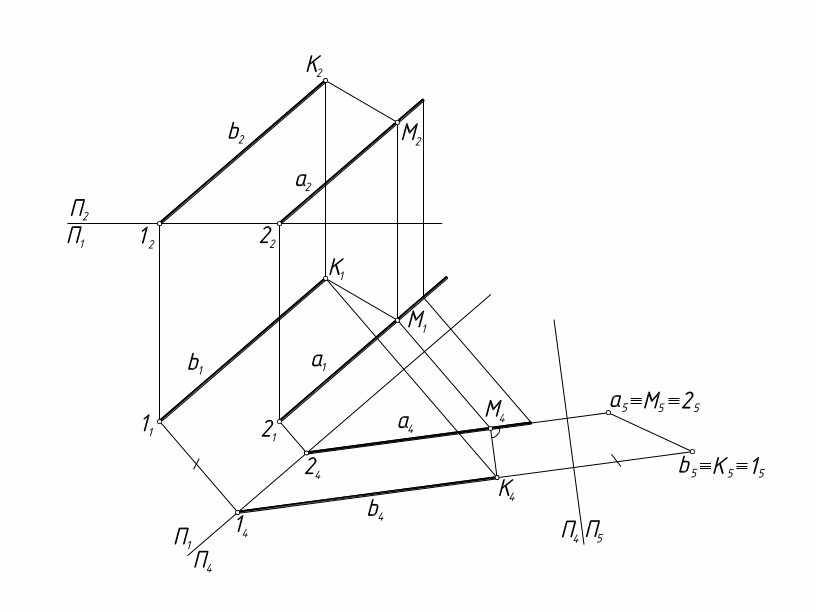
Рис. 16. Определение расстояния между параллельными прямыми
Решение. Сначала построено изображение прямых на плоскости П1 П4. В этой системе плоскостей прямые занимают положение линии уровня: а1(b1)|| П4 (рис. 16).
В системе плоскостей П4 П5 прямые занимают проецирующее по отношению к плоскости П5 положение: П5 а4(b4). Отрезок M5K5 между проекциями прямых определяет истинную величину расстояния между прямыми а и b.
