1.1. Метод замены плоскостей проекций. Четыре основные задачи на преобразование чертежа

Сущность способа замены плоскостей проекций: положение геометрических элементов в пространстве остается неизменным, а система П₁/П₂ дополняется плоскостями, образующими с П₁ или с П₂, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций. Каждая новая система выбирается так, чтобы получить положение, наиболее удобное для выполнения требуемого построения.

Прежде чем рассматривать метрические задачи, необходимо разобрать решение четырех основных задач преобразования чертежа.

Рассмотрим их решение способом замены плоскостей проекций.

Задача 1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.

Решение. Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П₄. От системы плоскостей П₁ П₂ перейти к системе П₁ П₄ или П₂ П₄. На чертеже новая ось проекций должна быть параллельной одной из заданных проекций прямой.

Н

Рис. 1. Первая задача на преобразование комплексного чертежа

а рис. 1 построено изображение прямой l (А В) общего положения в системе плоскостей П₁ П₄, причем П₄ || l₁. Новые линии связи A₁A₄ и В₁В₄ проведены перпендикулярно новой оси – П₁/П₄, параллельной горизонтальной проекции l₁. Новая проекция прямой А₄В₄ дает истинную величину отрезка АВ и позволяет определить угол наклона α прямой к горизонтальной плоскости проекций. Для других плоскостей проекций угол наклона прямой к ним определяется, если перейти к системе П₂ П₄ – угол наклона β к фронтальной плоскости проекций, либо в системе П₃ П₄ – угол наклона γ к профильной плоскости проекций.

Задача 2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.

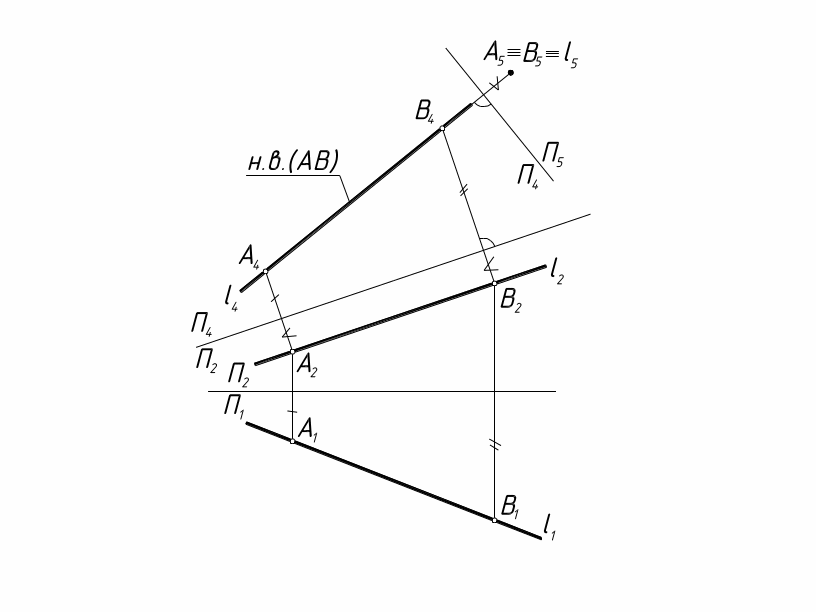
Рис. 2. Вторая задача на преобразование комплексного чертежа

Рис. 3. Преобразование прямой общего положения в проецирующую прямую

Решение. Чтобы на новой плоскости проекций изображение прямой было точкой, новую плоскость проекций располагают перпендикулярно данной

прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П₁ П₄ (рис. 2).

На рис. 3 сначала построено изображение прямой l₄ на плоскости П₂ П₄, расположенной параллельно прямой l₂. В системе плоскостей П₂ П₄ прямая заняла положение линии уровня (А₂А₄ П₂/П_4, П₂/П₄ || l₂). Затем от системы П₂ П₄ осуществлен переход в систему П₄ П₅, – вторая новая плоскость проекций П₅ l₄. Точки А и В прямой находятся на одинаковом расстоянии от плоскости П₄. На плоскости П₅ получаем изображение прямой в виде точ- ки (А₅ = B₅ = l₅).

Задача 3. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение.

Решение. Все линии этого уровня на новой плоскости проекций изобразятся точками. На рис. 4 в плоскости Δ построены горизонталь h (A 1) и новая плоскость проекций П₄ h₁. Графическое решение третьей задачи приводит к построению изображения плоскости в виде прямой линии, угол наклона которой к новой оси проекции П₁/П₄ определяет угол наклона α плоскости Δ (ABC) к горизонтальной плоскости проекций.

Рис. 4. Третья задача на преобразование комплексного чертежа

Задача 4. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня.

Р

Рис. 5. Четвертая задача на преобразование комплексного чертежа

ешение. При выполнении задачи определяют величину плоских фигур. Новую плоскость проекций располагают параллельно заданной плоскости Θ(ABC). Если исходное положение плоскости Θ было горизонтально проецирующим, то новое изображение строят в системе П₁ П₄. На рис. 5 построена новая проекция А₄В₄С₄ горизонтально проецирующей плоскости Θ(ABC) на плоскости П₄ П₁, это и есть натуральная величина Δ (ABC).

Если в исходном положении плоскость занимает общее положение, а нужно получить изображение ее как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно задачу 3, а затем –задачу 4.

Рис. 6. Преобразование плоскости общего положения в плоскость уровня

При первой замене плоскость становится проецирующей, а при второй – плоскостью уровня (рис. 6).

Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Итак, рассматривая метрические задачи, необходимо отметить, что любая из них может быть решена, если использовать решение одной из четырех основных задач на преобразования чертежа.