1.6 Вычисление пределов показательно-степенной функции.

Показательно степенной функцией называется функция вида . Чаще всего при вычислении пределов от показательно степенной функции получаются неопределенности . Так как о поведении такой функции в общем случае ничего сказать нельзя (а предел описывает поведение функции вблизи заданной точки), то при вычислении предела от такой функции рекомендуется ее представить иначе, при помощи основного логарифмического тожества: . Мы будем использовать частный случай этой формулы , здесь -это константа, приближенно равная 2,71, а и называется натуральным логарифмом. Используя такое представление, получим (последнее равенство справедливо в силу свойства логарифмов ), а это уже показательная функция. Теперь достаточно знать к чему стремится ее показатель, и будем знать, к чему стремится сама функция. При этом могут возникнуть следующие ситуации:

1) если конечен, то в силу непрерывности показательной функции предел с самой функции можно переносить на ее аргумент. Тогда ;

2) если , то получим ситуацию, которую символически можно записать так: . Учитывая поведение показательной функции, при условии, что ее показатель стремится к +∞, получим ;

3) если , то символически этот случай можно записать следующим образом: . Учитывая поведение показательной функции, получим .

Пример 1.13. Вычислить .

Решение. При дробь 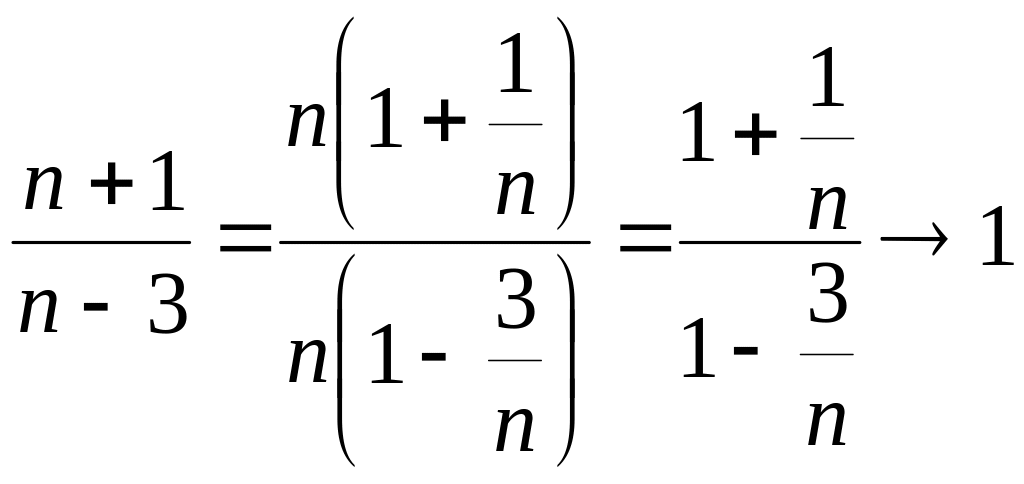, так как . Тогда мы имеем неопределенность и показательно степенную функцию по условию. Прежде всего представим ее в виде степенной на основании основного логарифмического тождества, получим

Вычислим предел от показателя отдельно. Заметим, что в числителе и знаменателе дроби, стоящей в аргументе логарифма стоят многочлены первой степени, а, значит такая дробь неправильная (неправильной рациональной дробью называется дробь, у которой числитель и знаменатель -- многочлены, причем старшая степень числителя не меньше старшей степени знаменателя). Из неправильной рациональной дроби можно выделить целую часть: (здесь мы использовали свойство почленного деления дроби ). Тогда . Заметим, что , тогда аргумент логарифма представлен в виде: единица плюс бесконечно малая функция, а тогда логарифм имеет эквивалентную функцию , то есть . В нашем пределе мы имеем право переходить к эквивалентным, так как имеем дело с произведением. Тогда получим .

Окончательно .

Пример 1.14. Вычислить

Решение. Как и в предыдущем примере, мы имеем дело с показательно-степенной функцией и неопределенностью . Перейдем снова к показательной функции, применив основное логарифмическое тождество:

Вычислим предел от показателя отдельно. Выясним: можно ли заменить логарифм эквивалентной функцией. Это возможно тогда, когда аргумент логарифма может быть представлен в виде единица плюс бесконечно малая функция. . Так как при , то аргумент логарифма представлен в нужном виде , и, значит . Тогда

.

Окончательно .