Некоторые свойства бесконечно больших и бесконечно малых функций.

1. Алгебраическая сумма конечного числа бесконечно малых функций при является бесконечно малой функцией при .

2. Произведение бесконечно малой при функции на функцию ограниченную в некоторой проколотой окрестности точки , является бесконечно малой функцией при .

3. Сумма бесконечно больших одного итого же знака при функций есть бесконечно большая того же знака при функция.

4. Произведение бесконечно большой при функции и функции, имеющей предел, отличный от нуля при есть бесконечно большая при функция.

Теорема 1.1 о связи между бесконечно большими и бесконечно малыми функциями. Если функция является бесконечно малой при и в некоторой проколотой окрестности точки , то функция является бесконечно большой при . И, наоборот, если функция является бесконечно большой при и в некоторой проколотой окрестности точки , то функция является бесконечно малой при .

Теорема 1.2 об арифметических операциях с пределами. Пусть -точка сгущения множества Х. Если существует конечные пределы , то , , если .

Итак, согласно этой теореме, если пределы двух функций конечны, то автоматически можно посчитать предел алгебраической суммы, произведения и частного (если предел знаменателя отличен от нуля). Рассмотрим те ситуации, которые исключены из условия этой теоремы.

1) Сумма.

А) Если одно из слагаемых имеет конечный предел ( ), другое – бесконечный ( ), тогда по свойству бесконечно больших функций предел их алгебраической суммы равен бесконечности. При помощи символов это можно записать следующим образом: .

Б) Если оба слагаемых имеют бесконечные пределы, то важно знать какого знака эти пределы. Если обе функции имеют бесконечные пределы одинаковых знаков ( или ), то по свойству бесконечно больших функций предел их суммы будет равен бесконечности того же знака. . Если обе функции являются бесконечно большими разных знаков ( ), то ничего определенного о пределе их суммы сказать нельзя (величина предела зависит от конкретного примера), ∞-∞ - неопределенность.

2) Произведение.

А) Если один из множителей имеет конечный предел, отличный от нуля, а другой множитель стремится к бесконечности ( ), то по свойству бесконечно больших функций предел произведения равен бесконечности: .

Б) Если оба множителя стремятся к бесконечности ( ), то по свойству бесконечно больших функций предел произведения равен бесконечности, при чем со знаком плюс (минус), если эти функции являются бесконечно большими одного знака (разного знака): .

В) Если же предел одного множителя равен нулю, у другого бесконечности ( ), то ничего определенного о пределе их произведения сказать нельзя: -неопределенность.

3) Частное.

А) Если , то предел их частного по теореме о связи между бесконечно малыми и бесконечно большими функциями будет равен бесконечности: , так как .

Б) Если , то предел их частного по теореме о связи между бесконечно малыми и бесконечно большими функциями будет равен нулю: .

Действительно,

С) Если наоборот , то предел их частного равен бесконечности: .

Д) Если же обе функции стремятся к нулю или бесконечности ( или ), то ничего определенного о пределе их частного сказать нельзя: - неопределенности.

Из всех выше проведенных рассуждений вытекают следующие ситуации (записанные в символьном виде), исключенные из теоремы об арифметических операциях с пределами, в которых можно дать ответ сразу:

(1) (4) (6)

(2) (5) (7)

(3) (8)

и неопределенности: .

Основная задача в этом разделе научиться раскрывать эти неопределенности. Рассмотрим ряд различных пределов и установим алгоритмы действий при той или иной неопределенности.

1.2 Раскрытие неопределенности вида .

Для раскрытия такой неопределенности необходимо в числителе и знаменателе дроби вынести за скобки то слагаемое, которое растет быстрее других (в частности, для многочленов это означает вынести слагаемое в наибольшей степени в числителе и знаменателе).

Пример 1.1. Вычислить предел числовой последовательности .

Решение. Мы уже знаем, что числовая последовательность—это частный случай функции, поэтому при вычислении таких пределов мы можем применять теорему об арифметических операциях с пределами и все рассуждения об исключительных ситуациях, проведенных нами выше. Исходя из этого, чтобы вычислить предел дроби, необходимо установить к чему стремятся ее числитель и знаменатель. Так как , то, очевидно, что и . При достаточно больших (уже при будет гораздо больше и, следовательно, . Так же по свойствам бесконечно больших функций . Получили, что числитель и знаменатель дроби стремятся к бесконечности, а, значит, мы имеем дело с неопределенностью вида . Тогда, следуя рекомендации, приведенной выше, нужно в числителе и знаменателе вынести за скобку неизвестное в наибольшей степени. В числителе –это , в знаменателе . Получим

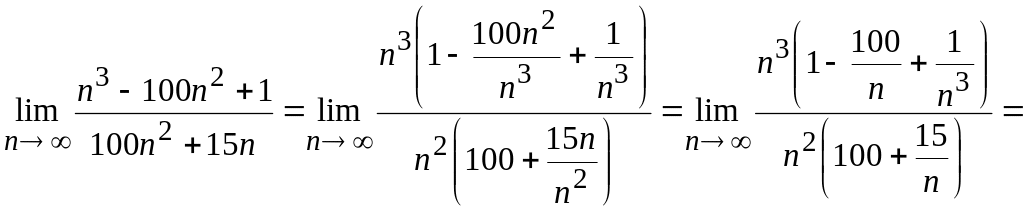
Теперь в числителе и знаменателе стоит произведение, а значит, дробь можно сократить на их общий множитель , получим

Так как , то из соотношения (7) . Тогда по теореме об арифметических операциях с функциями, имеющими конечные пределы , а . Следовательно, числитель полученной дроби представляет собой произведение бесконечно большой функции и функции , имеющей конечный предел, отличный от нуля. Тогда, учитывая соотношение (4) числитель будет стремиться к ∞: , а знаменатель стремится к 100. Тогда вся дробь, учитывая соотношение (8) будет стремиться к бесконечности:

. Итак, окончательно, .

Пример 1.2. Вычислить

Решение. При и . Значит перед нами снова неопределенность . Поэтому нужно снова вынести за скобку в числителе и знаменателе в наибольшей степени. Для того чтобы в числителе установить старшую степень, представим каждое слагаемое в виде степени: . Теперь видно, что старшая степень в числителе , а в знаменателе , выносим их за скобку

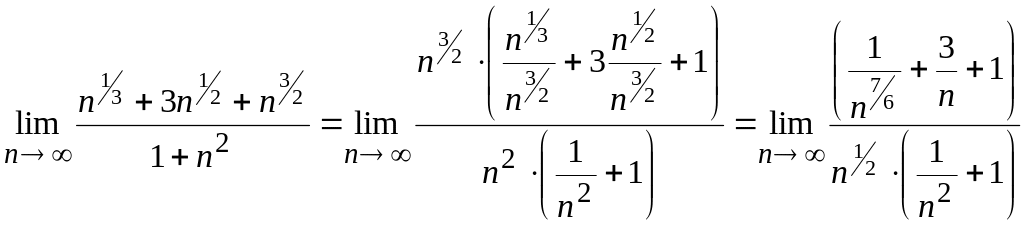
Теперь из соотношения (7) , а значит числитель ; . Тогда согласно (4) знаменатель , а вся дробь, учитывая (7) . Окончательно имеем .

Пример 1.3. Вычислить

Решение. Очевидно, что при числитель и знаменатель дроби стремятся к бесконечности, следовательно, здесь неопределенность . Снова в числителе и знаменателе нужно выносить в наибольшей степени. Так как выражение в знаменателе содержит корень, то вынесем в знаменателе старшую степень сначала под корнем (выносим ), получим

Далее к полученному выражению применим свойство арифметического корня , имеем . Теперь заметим, что в знаменателе два слагаемых, у первого порядок роста определяет , второе слагаемое—это константа 2(не растет), поэтому старшая степень знаменателя , в числителе, очевидно, тоже старшая степень . Следовательно, выносим за скобку в числителе и знаменателе дроби , получим

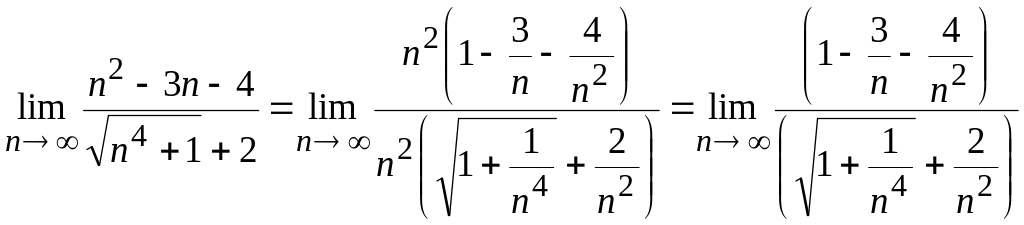
При числитель , и знаменатель , а, значит, вся дробь стремится к 1. Окончательно .