Лекция 4. Скалярное, векторное, смешанное произведение векторов.

Скалярное произведение векторов.

Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается скалярное произведение символом (  ) или .

Скалярное произведение векторов можно выразить формулами:

=I I I I cos( ( ))=I I = I I .

О тсюда скалярное произведение двух векторов равно произведению длины одного вектора на проекцию на него другого.

Пусть вектор перемещения будет неподвижен, а точка приложения вектора силы скользит вдоль вектора , тогда

=I I =I I I I cos=A

есть работа, совершаемая под действием силы вдоль вектора .

Скалярное произведение векторов, заданных своими координатами.

Пусть ={x₁, y₁, z₁} и ={x₂, y₂ z₂,} тогда = x₁ x₂+y₁ y₂+z₁ z₂ .

Скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат.

Свойства скалярного произведения.

1. Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы ортогональны: =0 = .

2. Скалярное произведение коммутативно: = .

3. Скалярное произведение ассоциативно относительно скалярного множителя: ( ) = ( ).

4. Скалярное произведение дистрибутивно: ( + )=( )+( ).

5. Свойство скалярного квадрата: ²=I I² отсюда I I= .

Рассмотрим таблицу скалярного умножения ортов:

( ; )=( ; )=( ; )=1, ( ; )=( ; )=( ; )=( ; )=( ; )=( ; )=0.

Скалярное произведение одноименных ортов равно единице, а разноименных - нулю.

Угол между двумя векторами. Из определения скалярного произведения:

cos= = .

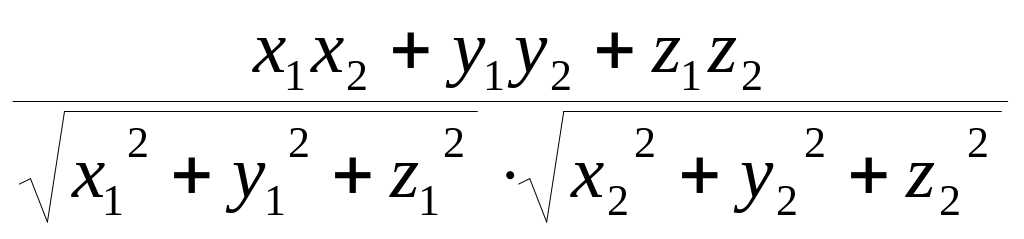Условие ортогональности двух векторов:

x₁ x₂+y₁ y₂+z₁ z₂=0.

Условие коллинеарности двух векторов: .

Проекция вектора на вектор:

.

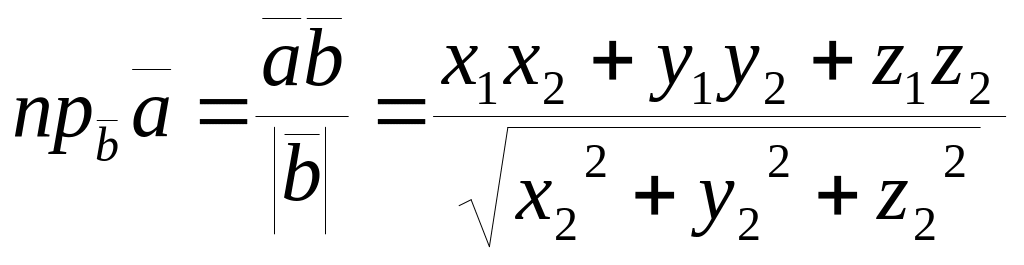Векторное произведение.

Определение. Векторным произведением вектора на вектор называется вектор , или , определяемый следующими тремя условиями:

1. Модуль вектора равен , где - угол между векторами и , т.е.

l l= .

Отсюда следует, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах и как на сторонах.

2. Вектор перпендикулярен к каждому из векторов и (  ;  ), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах и .

3. Вектор направлен так, что если смотреть из его конца, кратчайший поворот от вектора к вектору был бы против часовой стрелки. (векторы , , образуют правую тройку).

Векторное произведение двух векторов, заданных своими проекциями.

Пусть даны векторы =x₁ +y₁ +z₁ и = x₂ +y₂ +z₂ , тогда

= .

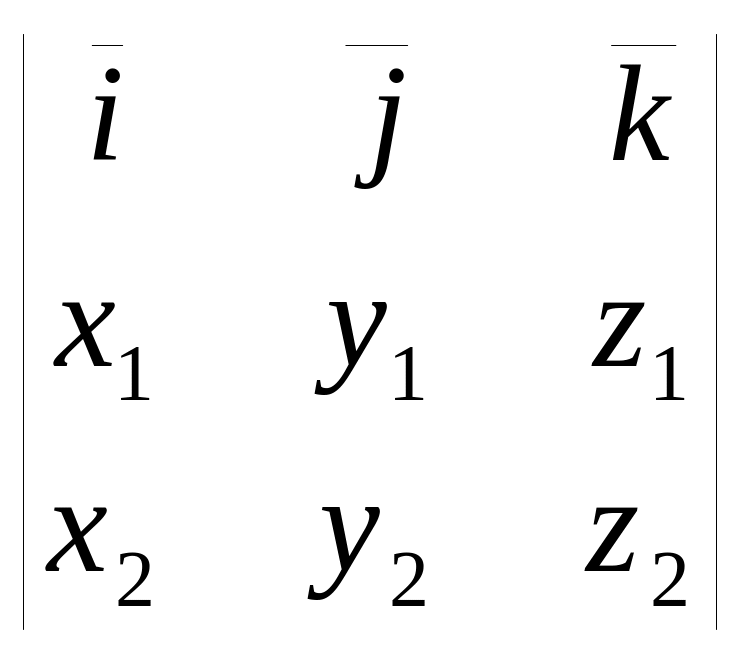Если разложить определитель по элементам первой строки, то

= .

Механический смысл векторного произведения.

П усть в точке А к диску приложена сила . Определить момент силы относительно точки О на диске - =mom₀ .

 и  и (), l l=l lp=l ll lsin(-)=l ll lsin().

О тсюда следует, что =

Свойства векторного произведения векторов.

1. Векторное произведение коллинеарных векторов равно нулю.

ll ( l l0; l l0) =0.

2. Антикоммутативность: = - .

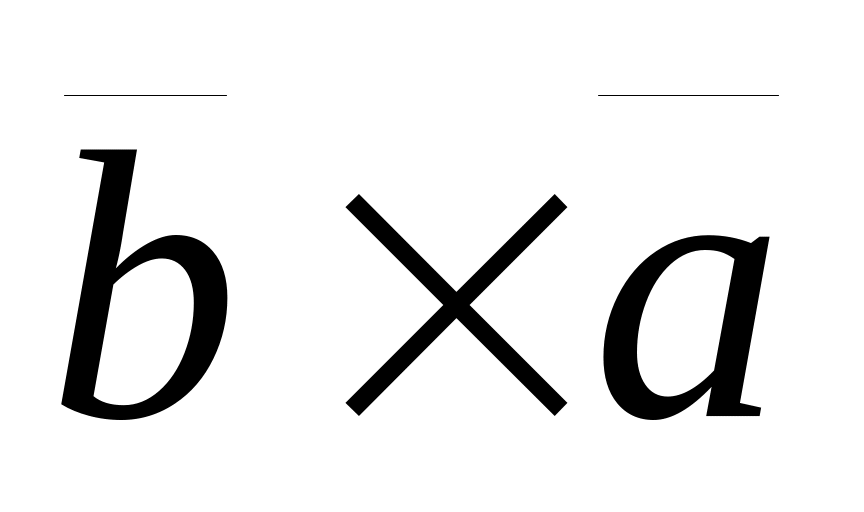3. Ассоциативность относительно скалярного множителя: ( )=( ).

4. Дистрибутивность: = + .

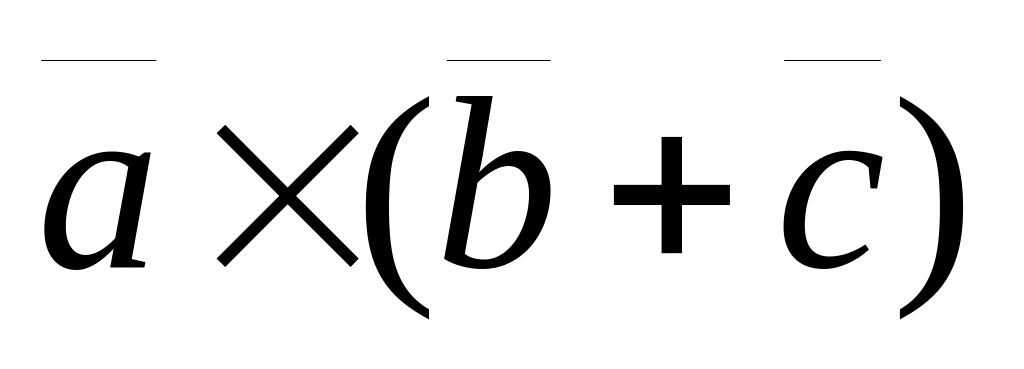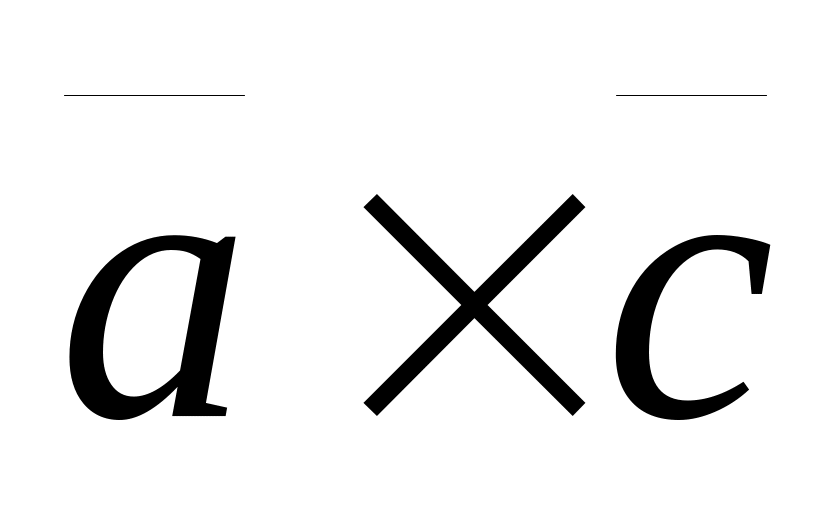Таблица векторного умножения ортонормированного базиса , , .

 =  =  =0,  = ,  = ,  = ,  = - ,  = - ,  = - .

Д ля запоминания можно воспользоваться круговым правилом: