П онятие о проекциях.

Пусть дан вектор и ось OL, - угол между вектором и положительным направлением оси OL. и -основания перпендикуляров, опущенных из точек А и В соответственно.

Определение. Проекцией вектора на ось называется длина отрезка оси A^lB^l, взятая со знаком плюс, если вектор образует острый угол с направлением оси, и со знаком минус в противоположном случае.

Теорема. Проекция вектора на ось OL равна произведению длины вектора на косинус угла между вектором и осью: =I I cos.

Следствие. При умножении вектора на некоторое число  его проекция умножается на это же число: =  .

Теорема о проекции суммы. Проекция суммы некоторого числа векторов на ось(L) равна сумме проекций слагаемых векторов: = + + , = + + .

Декартова система координат.

Точка- начало координат О(0,0,0). Ортонормированный базис образуют взаимно перпендикулярные векторы , , единичной длины, т.е. l l=l l=l l=1 и ( ^ )=( ^ )=( ^ )= . Прямые, проходящие через начало координат в направлении векторов , , называются осями координат. Векторы , , соответствуют положительному направлению осей координат: OX, OY, OZ - оси абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями OXY, OXZ, OYZ.

Определение. Прямоугольной системой координат называется совокупность точки (О) и ортонормированного базиса.

Определение. Радиус-вектором произвольной точки М по отношению к точке О, называется вектор . Точке М можно сопоставить упорядоченную тройку чисел (x,y,z)- компоненты ее радиус-вектора: М(x, y, z) и = ={x,y,z}.

О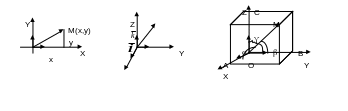 пределение. Компоненты радиус-вектора точки М по отношению к началу координат называют координатами точки М в рассматриваемой системе координат.

M(x,y,z)

O j

X

рис. 1 рис. 2

Координаты вектора совпадают с проекцией вектора на соответствующие оси координат (рис.1):

x= , y= , z= , =x +y +z , ={x,y,z} (рис. 1).

Из рис. 2 имеем: = = = x +y +z , OA=x, OB=y, OC=z,

l l= = .

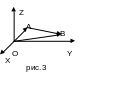
Пусть вектор задан координатами крайних точек = , А(x₁,y₁,z₁)

и В(x₂,y_2,z₂) (рис.3), тогда

Следовательно, чтобы определить координаты вектора по координатам крайних точек, надо из координат конца вычесть соответствующие координаты начала: ={x₂-x₁, y₂-y₁, z₂-z₁ }.

Определение. Пусть , , - углы между вектором и соответственно ортами , , (рис. 2), тогда направляющие косинусы вектора r определяются по правилу:

соs = = , соs= = , соs= = ,

Следовательно, сумма квадратов направляющих косинусов равна 1: cos²+cos²+cos²=1.

Связь компонент, проекций, направляющих косинусов и коэффициентов в разложении по базису.

Пусть вектор ={x, y, z} в пространстве R³; , , -ортонормированный базис в данной системе координат, , , - углы между вектором и соответственно ортами , , , тогда =x +y +z , где x , y , z -составляющие вектора ,

x, y, z- координаты вектора в базисе , , ,

x= =l lCos, y= =l lCos, z= =l lCos.

Деление отрезка в данном отношении.

Пусть А(x₁,y_1,z₁), B(x₂,y₂,z₂). Координаты точки С(x,y,z) на отрезке АВ, которая делит этот отрезок в отношении , т.е. , определяются по формулам:

x= , y= , z= .

Координаты середины отрезка АВ соответствуют значению =1 и определяются как полусумма координат концов отрезка:

x= , y= , z= .

Линейные операции над векторами, заданными своими координатами.

Пусть ={x₁, y₁, z₁} и ={x₂, y₂, z₂}.

1. При умножении вектора на число каждая координата вектора умножается на это число: = , R, тогда ={ x₁, y₁, z₁}.

2. При сложении (вычитании) векторов их одноименные проекции складываются (вычитаются): = + , тогда ={ x₁+x₂, y₁+y₂, z₁+z₂}.