
- •Расчет аналоговых и цифровых фильтров
- •Содержание
- •1. Общая теория
- •1.1. Свойства цифровых фильтров
- •1.2. Представление цифрового фильтра в виде разностного уравнения
- •1.3 Аналоговые фильтры-прототипы
- •1.3.1. Фильтры Баттерворта
- •1.3.2. Фильтры Чебышева
- •1.3.3. Эллиптические фильтры
- •1.3.4. Фильтры Бесселя
- •1.4. Преобразования полосы частот для аналоговых фильтров
- •1.5. Преобразование полосы для цифровых фильтров
- •1.6. Методы дискретизации аналогового фильтра
- •1.6.1. Метод инвариантного преобразования импульсной характеристики
- •1.6.2. Метод билинейного преобразования
- •1.7. Методы синтеза ких-фильтров.
- •1.7.1. Прямоугольное окно
- •1.7.2. Обобщенное окно Хэмминга
- •1.7.3. Окно Блэкмана
- •1.7.4. Окно Кайзера
- •1.8. Методы синтеза бих-фильтров.
- •1.9. Методы реализации цифровых фильтров
- •1.9.1. Прямая форма
- •1.9.2. Прямая каноническая форма
- •1.9.3. Каскадная форма
- •1.9.4. Параллельная форма
- •2. Задание на курсовую работу в таблице 2.1. Представлены варианты на курсовую работу. Вариант выбрается в соответсвии с указанием преподавателя.
- •3. Порядок выполнения задания №1. Расчет аналогового фильтра.
- •Порядок фильтра.
- •Аппроксимация ачх фильтров - общие замечания.
- •Аппроксимация по Баттерворту.
- •Аппроксимация по Чебышеву первого рода.
- •Аппроксимация по Чебышеву второго рода.
- •Аппроксимация по Кауэру. Эллиптический фильтр.
- •Сравнение порядков фильтров при различных способах аппроксимации ачх. Решение уравнения порядка фильтра.
- •Порядок расчет первого задания.
- •4. Порядок выполнения задания №2. Расчет цифрового фильтра методом частотной выборки с использованием окон.
- •Порядок расчет второго задания.
- •5. Порядок выполнения задания №3. Реализация цифрового фильтра в среде Simulink.
- •6. Проектирование цифровых фильтров в среде matlab
- •6.1. Анализ фильтров и выполнение
- •Filtic – cоздание начального состояния для функции filter:
- •Freqs – частотная характеристика аналогового фильтра:
- •Freqspace – формирование последовательности отсчетов частоты:
- •Freqz – частотная характеристика цифрового фильтра.
- •Grpdelay – групповая задержка цифрового фильтра:
- •Impz – импульсный отклик цифрового фильтра:
- •Unwrap – корректировка фазовых углов:
- •Zplane – отображение нулей и полюсов цифрового фильтра:
- •7.2. Проектирование цифровых бих-фильтров besself – проектирование аналогового фильтра Бесселя:
- •Butter – проектирование цифрового и аналогового фильтров Баттерворта:
- •Cheby1 – проектирование цифрового и аналогового фильтров Чебышева – первого типа:
- •Cheby2 – проектирование цифрового и аналогового фильтров Чебышева второго типа:
- •Ellip – проектирование эллиптического цифрового и аналогового фильтров:
- •Yulewalk – проектирование рекурсивного фильтра с использованием метода наименьших квадратов по заданной амплитудно-частотной характеристике:
- •7.3. Выбор порядка бих-фильтра buttord – выбор порядка фильтра Баттерворта:
- •Cheb1ord – выбор порядка для фильтра Чебышева первого порядка:
- •Cheb2ord – выбор порядка для фильтра Чебышева первого порядка:
- •Ellipord – выбор порядка эллиптического фильтра:
- •7.4. Проектирование ких-фильтров fir1 – фильтр fir проектируется с использованием метода окна:
- •Fir2 – проектирование фильтра fir с использованием оконного метода для произвольной формы фильтра:
- •Firls – проектирование ких-фильтра с использованием минимизации ошибок методом наименьших квадратов (мнк):
- •Intfilt – расчет интерполирующего ких-фильтра:
- •Remez – синтез оптимального fir-фильтра с равномерной (чебышевской) аппроксимацией на основе алгоритма Паркса – Мак-Клелана:
- •7.5. Преобразования
- •Dftmtx – матрица дискретного преобразования Фурье (дпф):
- •Impinvar – метод инвариантной импульсной характеристики для перевода аналогового фильтра в цифровой:
- •Список литературы
1.7. Методы синтеза ких-фильтров.
Фильтр, импульсная характеристика которого является последовательностью конечной длины, называют фильтром с конечной импульсной характеристикой, или КИХ-фильтром.
Такой фильтр всегда можно сделать физически реализуемым, введя необходимую задержку импульсной характеристики. Если все элементы импульсной характеристики конечны, то КИХ-фильтр всегда устойчив, так как проверка на устойчивость сводится к суммированию конечного числа ограниченных слагаемых. Более того, КИХ-последовательности можно выбрать так, чтобы фильтры имели строго линейные фазовые характеристики. Поэтому, используя КИХ-последовательности, можно проектировать фильтры с произвольной амплитудной характеристикой.
Известны три класса методов расчета КИХ-фильтров с линейной фазой:
методы взвешивания с помощью окна;
методы частотной выборки;
методы оптимальных (по Чебышеву) фильтров.
В настоящем пособии рассматривается только первый метод как наиболее просто реализуемый.
Частотная характеристика любого цифрового фильтра является периодической функцией частоты, поэтому ее можно представить рядом Фурье:
![]() ,
,
где
![]() .
.
Видно, что коэффициенты Фурье
![]() совпадают с коэффициентами импульсной
характеристики цифрового фильтра.
Используя для проектирования КИХ-фильтров
соотношение (1.1), можно столкнуться с
двумя трудностями. Во-первых, импульсная
характеристика фильтра имеет бесконечную
длину, поскольку суммирование в (1.1)
производится в бесконечных пределах.
Во-вторых, фильтр физически не реализуем,
так как импульсная характеристика
начинается в
совпадают с коэффициентами импульсной
характеристики цифрового фильтра.
Используя для проектирования КИХ-фильтров
соотношение (1.1), можно столкнуться с
двумя трудностями. Во-первых, импульсная
характеристика фильтра имеет бесконечную
длину, поскольку суммирование в (1.1)
производится в бесконечных пределах.
Во-вторых, фильтр физически не реализуем,
так как импульсная характеристика
начинается в
![]() ,
т. е. никакая конечная задержка не сделает
фильтр физически реализуемым.
,
т. е. никакая конечная задержка не сделает
фильтр физически реализуемым.
Один из возможных методов
получения КИХ-фильтра, аппроксимирующего
заданную функцию
![]() ,
заключается в усечении бесконечного
ряда Фурье за
,
заключается в усечении бесконечного
ряда Фурье за
![]() .
Однако простое усечение ряда приводит
к явлению Гиббса, которое проявляется
в виде выбросов и пульсаций определенного
уровня до и после точки разрыва в
аппроксимируемой частотной характеристике.
.
Однако простое усечение ряда приводит
к явлению Гиббса, которое проявляется
в виде выбросов и пульсаций определенного
уровня до и после точки разрыва в
аппроксимируемой частотной характеристике.
Лучшие характеристики дает
метод проектирования КИХ-фильтров,
основанный на использовании весовой
последовательности конечной длины
![]() ,
называемой окном, для модификации
коэффициентов Фурье
в формуле (1.1) с тем, чтобы управлять
сходимостью ряда Фурье.
,
называемой окном, для модификации
коэффициентов Фурье
в формуле (1.1) с тем, чтобы управлять
сходимостью ряда Фурье.
Уменьшение эффекта Гиббса при использовании оконного сглаживания
Простота и высокая вычислительная эффективность метода частотной выборки делает его очень привлекательным для практического использования, однако на выходе получается фильтр с очень высоким уровнем боковых лепестков в полосе заграждения и неравномерностью в полосе пропускания, что привело к необходимости доработки метода частотной выборки для практического применения.
Отметим, что такие боковые лепестки возникают ввиду резкого перехода от частоты пропускания к частоте подавления и возникают из-за интерполяции дискретизированного комплексного коэффициента передачи фильтра.
Рассмотрим основные виды окон, используемых при синтезе КИХ-фильтров.
1.7.1. Прямоугольное окно
N-точечное прямоугольное окно соответствует простому усечению ряда Фурье. Оно описывается весовой функцией:
![]()
Частотная характеристика прямоугольного окна описывается соотношением
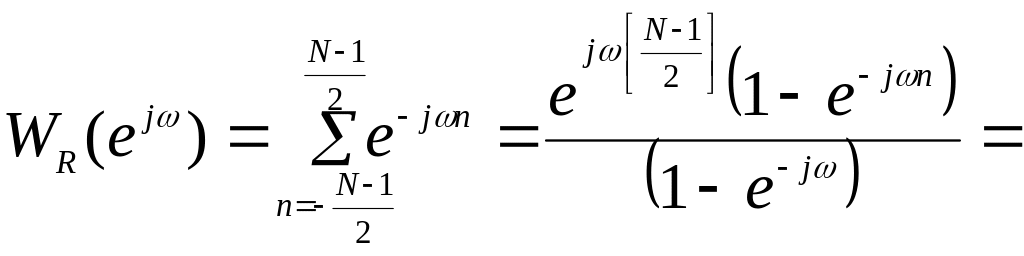
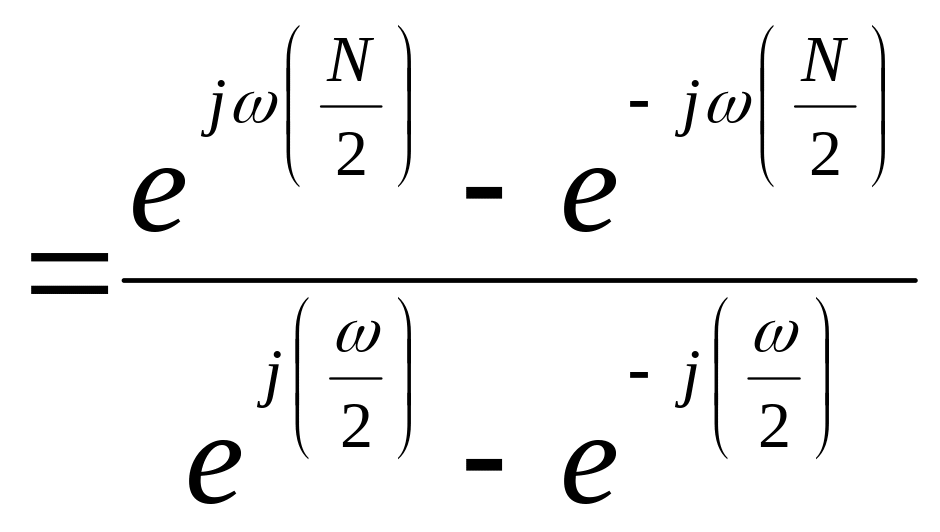 .
.
Таким образом,
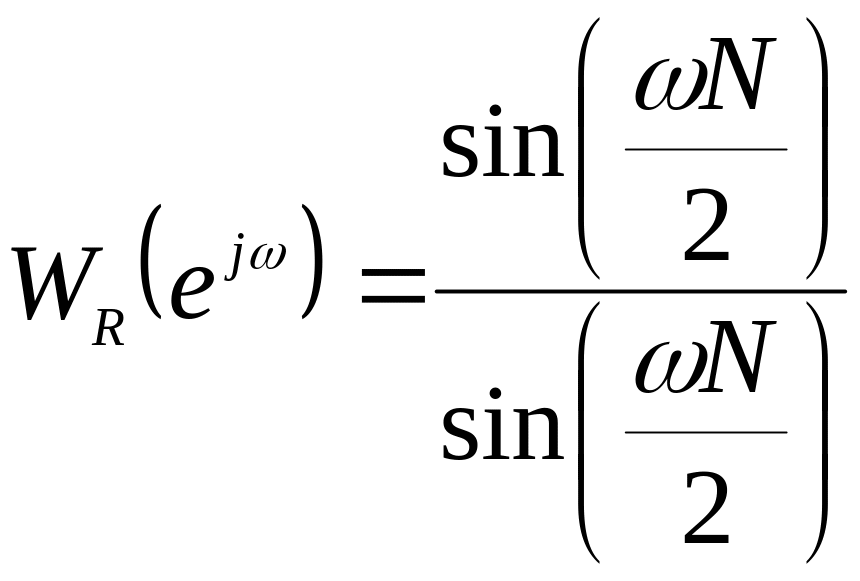 .
.
