1.1. Свойства цифровых фильтров

1. Цифровой фильтр называется стационарным, если его параметры не изменяются во времени, т. е. предварительно невозбужденный фильтр, в котором = = 0 при всех < 0, называют стационарным тогда и только тогда, когда для всех возможных воздействий.

2. Цифровой фильтр называют линейным тогда и только тогда, когда для всех и – произвольных постоянных и для всех допустимых воздействий и .

3. Цифровой фильтр называют физически реализуемым, если величина отклика при зависит только от значений входной последовательности с номерами . Это означает, что импульсная характеристика равна нулю при .

4. Цифровой фильтр называется устойчивым тогда и только тогда, когда реакция на ограниченное воздействие ограничена, т. е. если из при всех следует при всех . Необходимым и достаточным условием устойчивости фильтра является следующее требование к его импульсной характеристике:

1.2. Представление цифрового фильтра в виде разностного уравнения

Цифровой фильтр в общем виде представляется следующим образом как разностное уравнение:

(1.2)

где и – вещественные или комплексные коэффициенты.

Цифровые фильтры принято делить на два класса: нерекурсивные (НФ) и рекурсивные (РФ). Если в (1.2) все коэффициенты = 0, что соответствует отсутствию обратной связи, то фильтр является нерекурсивным и описывается уравнением

. (1.3)

Если в (1.3) хотя бы один из коэффициентов , то фильтр является рекурсивным и представляет собой устройство с обратной связью.

Для анализа систем, описываемых разностными уравнениями, широко применяется -преобразование. Прямое -преобразование последовательности определяется формулой

. (1.5)

В разностных уравнениях существенной операцией является единичная задержка, описываемая оператором , или (т. е. для последовательности -преобразование будет иметь вид

Передаточной (системной) функцией цифрового фильтра называется отношение -преобразований выходного и входного сигналов фильтра. Для рекурсивного и нерекурсивного фильтров из (1.3) и (1.4), используя (1.5), получаем:

Комплексная частотная характеристика цифрового фильтра, представленного в виде разностного уравнения (1.2), может быть получена подстановкой в выражение для передаточной функции значения . Для рекурсивного фильтра общего вида частотная характеристика будет иметь вид

Аналогично, для нерекурсивного фильтра имеем:

1.3 Аналоговые фильтры-прототипы

Приведем расчетные формулы для нескольких стандартных типов аналоговых фильтров. Допустим, нужно рассчитать аналоговый фильтр нижних частот с частотой среза рад/с. В качестве аппроксимируемой функции будет использоваться квадрат амплитудной характеристики (исключением является фильтр Бесселя).

Будем считать, что передаточная функция аналогового фильтра является рациональной функцией переменной s следующего вида:

1.3.1. Фильтры Баттерворта

Фильтры Баттерворта нижних частот характеризуются тем, что имеют максимально гладкую амплитудную характеристику в начале координат в s-плоскости. Квадрат амплитудной характеристики нормированного (т. е. имеющего частоту среза 1 рад/с) фильтра Баттерворта равен

где – порядок фильтра. Аналитически продолжая функцию на всю -плоскость, получим:

Все полюсы этой функции находятся на единичной окружности на одинаковом расстоянии друг от друга в -плоскости. Выразим передаточную функцию через полюсы, располагающиеся в левой полуплоскости s:

где , – константа нормирования.

Можно сформулировать несколько свойств фильтров Баттерворта нижних частот:

• Фильтры Баттерворта имеют только полюсы (все нули передаточных функций этих фильтров расположены на бесконечности).

• На частоте 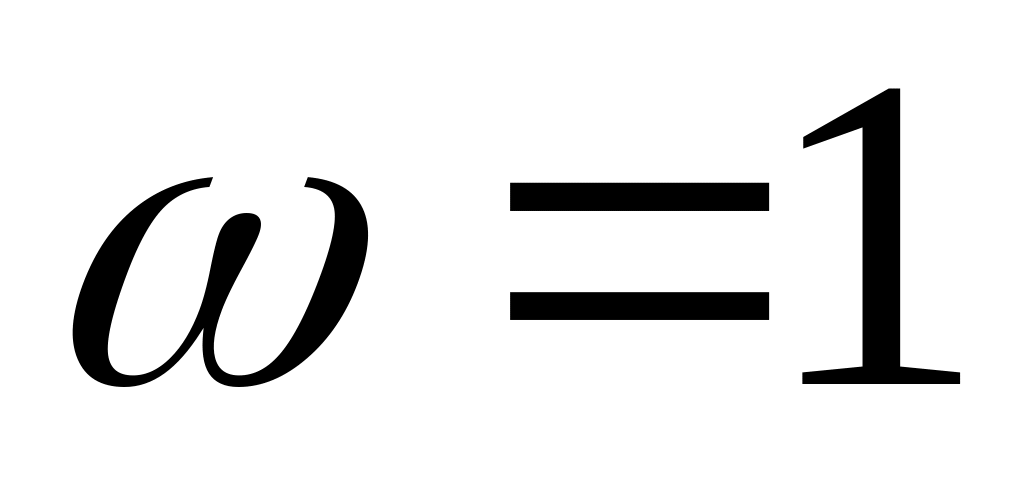рад/с коэффициент передачи фильтра равен (т. е. на частоте среза их амплитудная характеристика снижается на 3 дБ).

• Порядок фильтра n полностью определяет весь фильтр.