Методы математической статистики Параметрическое описание поведения случайной величины
При параметрическом описании поведение случайной величины определяется значениями специальных характеристик - параметров или моментов случайной величины.
Основной характеристикой является первый начальный момент, который называется МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ СЛУЧАЙНОЙ ВЕЛИЧИНЫ (МО):
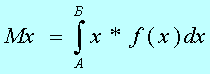
где: Mx - значение математического ожидания случайной величины x; A,B - пределы интегрирования (A - минус бесконечность, B - плюс бесконечность); f(x) - функция плотности вероятности случайной величины x. Для дискретной случайной величины интеграл превращается в сумму. Математическое ожидание характеризует центр, относительно которого группируются значения случайной величины.
Другими параметрами случайной величины являются ЦЕНТРАЛЬНЫЕ МОМЕНТЫ. Центральным моментом порядка k называется математическое ожидание отклонения значений случайной величины от центра в степени k:
Rk(x) = M[(x-Mx)k],
Доказано, что если функция плотности распределения случайной величины имеет одну вершину (функция унимодальна), то для полного описания поведения этой случайной величины достаточно указать МО и центральные моменты второго, третьего и четвертого порядка. Последние три характеристики имеют специальные названия. Второй центральный момент называется ДИСПЕРСИЕЙ: Dx = M[(x-Mx)2]. Дисперсия характеризует разброс значений случайной величины относительно МО. Обратите внимание, дисперсия всегда больше нуля. Третий центральный момент называется АСИММЕТРИЕЙ: Ax = M[(x-Mx)3]. Асимметрия характеризует "косость" графика функции плотности вероятности случайной величины. При Ax = 0 абсцисса вершины графика функции f(x) совпадает с МО (график симметричен). Если Ax < 0, то вершина этого графика расположена левее МО, при Ax > 0 вершина расположена правее МО. Четвертый центральный момент называется ЭКСЦЕССОМ: Ex = M[(x-Mx)4]. Этот момент характеризует "островершинность" графика f(x) и его значение всегда больше нуля. Наиболее распространенным в природе, а следовательно и наиболее часто применяемом для описания вероятностных процессов, является нормальный закон распределения. Для полного параметрического описания поведения случайной величины при нормальном законе распределения достаточно задания только двух параметров: математического ожидания и дисперсии. Асимметрия и эксцесс при нормальном законе распределения определяются через эти два параметра.
Методы математической статистики Свойства математического ожидания. Свойства дисперсии.
Напомним, что МО является интегральной характеристикой, поэтому свойства этого параметра определяются свойствами интеграла:
Математическое ожидание любой случайной величины независимо от вида распределения, которому она подчиняется и обладает следующими свойствами.
1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ РАВНО ЭТОЙ ВЕЛИЧИНЕ. Пусть а - неслучайная величина. Тогда М(a)=a 2. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СУММЫ НЕСЛУЧАЙНОЙ И СЛУЧАЙНОЙ ВЕЛИЧИН РАВНО СУММЕ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ И МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ СЛУЧАЙНОЙ ВЕЛЧИНЫ. Пусть а - неслучайная величина. Тогда М(a+x)=a+M(x). 3. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ПРОИЗВЕДЕНИЯ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ НА СЛУЧАЙНУЮ РАВНО ПРОИЗВЕДЕНИЮ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ НА МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ. Пусть а - неслучайная величина. Тогда М(a*x)=a*M(x). 4. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН РАВНО СУММЕ МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ ЭТИХ ВЕЛИЧИН. Пусть x и у - случайные величины. Тогда М(x+y)=M(x)+M(y). Обобщением перечисленных свойств является следующее: если a,b - неслучайные величины, x и y - случайные величины, то M(a*x+b*y)=a*M(x)+b*M(y). Хотя свойства рассмотрены для непрерывных случайных величин, они очевидно справедливы для дискретных случайных величин.