
- •1. Аксиоматика 3
- •2. Множества 4
- •3. Аналитическая геометрия 14
- •4. Векторная алгебра 25
- •5. Матрицы и определители 30
- •Аксиоматика
- •Аксиоматический метод построения математики
- •Математический язык
- •Множества
- •Понятие множества
- •Пустое множество
- •Числовые множества
- •Подмножества
- •Пересечение множеств
- •Объединение множеств
- •Вычитание множеств
- •Аналитическая геометрия
- •Система координат на плоскости и в пространстве
- •Расстояние между двумя точками на плоскости
- •Уравнение линии. Уравнение прямой с угловым коэффициентом
- •Уравнение – уравнение прямой с угловым коэффициентом k
- •Общее уравнение прямой
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой, проходящей через данную точку
- •Уравнение прямой, проходящей через две данные (различные) точки и
- •Полярные координаты
- •Угол между прямыми
- •Уравнение окружности
- •Эллипс. Каноническое уравнение эллипса
- •Гипербола. Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение параболы
- •У равнение сферы
- •Векторная алгебра
- •Понятие вектора
- •Коллинеарные векторы
- •Операции над векторами
- •Угол между векторами
- •Проекция вектора на ось
- •Скалярное произведение двух векторов
- •Координаты вектора
- •Разложение векторов
- •Действия над векторами, заданным координатами в пространстве
- •Матрицы и определители
- •Матрицы
- •Определители
- •Определители третьего порядка
- •Миноры и алгебраические дополнения матрицы
- •Обратная матрица
- •Системы линейных уравнений
- •Формулы Крамера
- •Матричный способ решения систем линейных уравнений
- •Метод Гаусса
- •Функции
- •Понятие функции
- •Способы задания функции
- •Обзор элементарных функций и их графиков
- •Пределы
- •Предел последовательности
- •Предел функции
- •Непрерывность функции
- •Производная
- •Определение производной
- •Правила дифференцирования
- •Производные высших порядков
- •Применение производной для исследования функции
- •Неопределенный интеграл
- •Способы интегрирования
- •О пределенный интеграл
- •Дифференциальные уравнения
- •Основные понятия:
- •Признаки сходимости ряда:
- •Ряды по степени разности
- •Теория вероятностей
- •Основные понятия теории вероятностей
- •Классическое определение вероятности
- •Геометрические вероятности
- •Алгебра событий
- •Теорема сложения вероятностей двух несовместимых событий
- •Теорема умножения вероятностей.
- •Теорема сложения вероятностей совместимых событий
- •Формула полной вероятности
- •Теорема умножения вероятностей независимых событий:
- •Дискретные случайные величины
- •Закон распределения дискретных случайных величин
- •Функция распределения случайной величины
- •Нормальное распределение
- •Числовые характеристики случайных величин
- •Свойства математического ожидания (мо) дискретной случайной величины:
- •Дисперсия дискретной случайной величины
- •Среднее квадратичное отклонение (стандартное)
- •Системы двух случайных величин и их числовые характеристики
- •Литература
Расстояние между двумя точками на плоскости
Д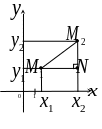 ано:
ано:
![]() и
и
![]() .
.
Найти
![]() .
.
Рассмотрим
![]() .
По теореме Пифагора:
.
По теореме Пифагора:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
Уравнение линии. Уравнение прямой с угловым коэффициентом
О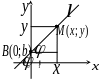 пределение:
уравнением линии на плоскости в
прямоугольной системе координат
пределение:
уравнением линии на плоскости в
прямоугольной системе координат
![]() называется уравнение
называется уравнение
![]() ,
которому удовлетворяют координаты
каждой точки данной линии и не
удовлетворяют координаты любой точки
плоскости, не лежащей на этой линии.
,
которому удовлетворяют координаты
каждой точки данной линии и не
удовлетворяют координаты любой точки
плоскости, не лежащей на этой линии.
Замечание: геометрическим образом заданного уравнения не всегда является линия:
![]() – точка
– точка
![]() ;
;
![]() – нет такой точки.
– нет такой точки.
Уравнение – уравнение прямой с угловым коэффициентом k
Дана
прямая
![]() ,
которая пересекает оси координат и не
параллельна ни одной из них. Пусть угол
наклона к положительному направлению
оси Ox равен
,
которая пересекает оси координат и не
параллельна ни одной из них. Пусть угол
наклона к положительному направлению
оси Ox равен
![]() .
Угол
отсчитывается от Ox против часовой
стрелки
.
Угол
отсчитывается от Ox против часовой
стрелки
![]() (
(![]() )
– угол наклона прямой
к положительному направлению оси Ox.
Точка пересечения с Oy –
)
– угол наклона прямой
к положительному направлению оси Ox.
Точка пересечения с Oy –
![]() .
.
Пусть
![]() – произвольная точка
.
Рассмотрим
– произвольная точка
.
Рассмотрим
![]() .
Он прямоугольный и имеет острый угол
;
.
Он прямоугольный и имеет острый угол
;
![]() ;
;
![]() .
Найдем
.
Найдем
![]() (отношение противолежащего катета к
прилежащему).
(отношение противолежащего катета к
прилежащему).
![]() .
Обозначим
через
.
Обозначим
через
![]() .
Имеем:
.
Имеем:
![]() или
или
![]() ,
,
![]() – уравнение
прямой с угловым коэффициентом
.
– уравнение
прямой с угловым коэффициентом
.
Ч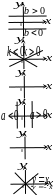 астные
случаи:
астные
случаи:
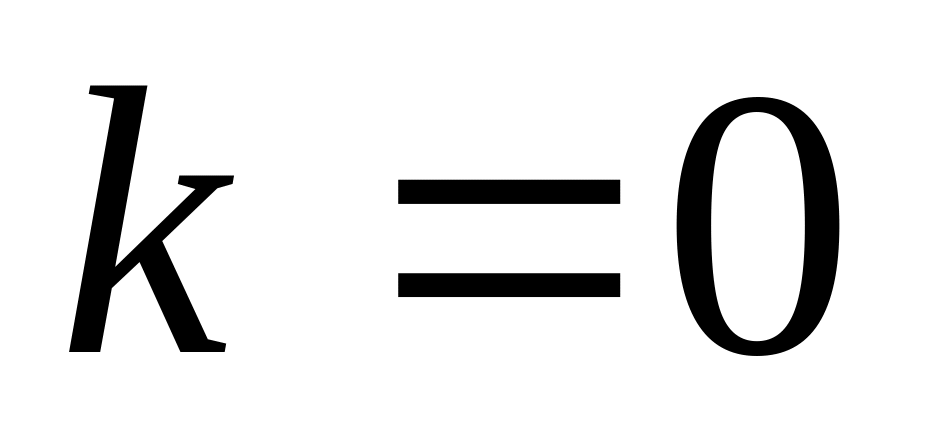 ,
,
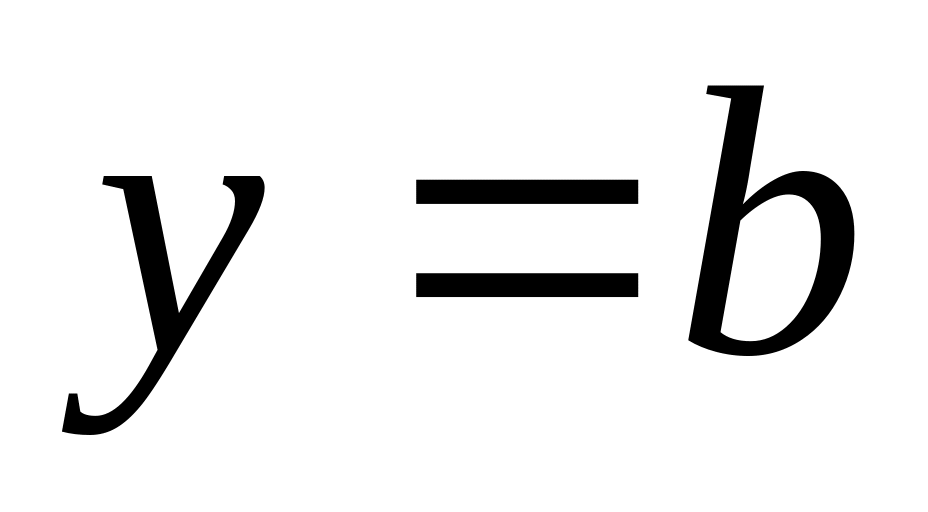 –
уравнение прямой, параллельной оси
Ох и отстоящей от нее на
–
уравнение прямой, параллельной оси
Ох и отстоящей от нее на
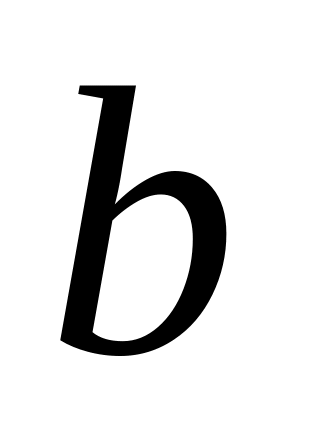 ;
;
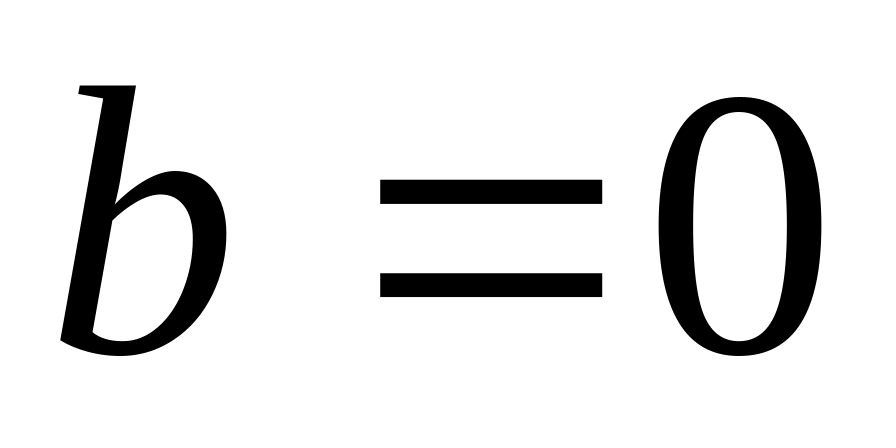 ,
,
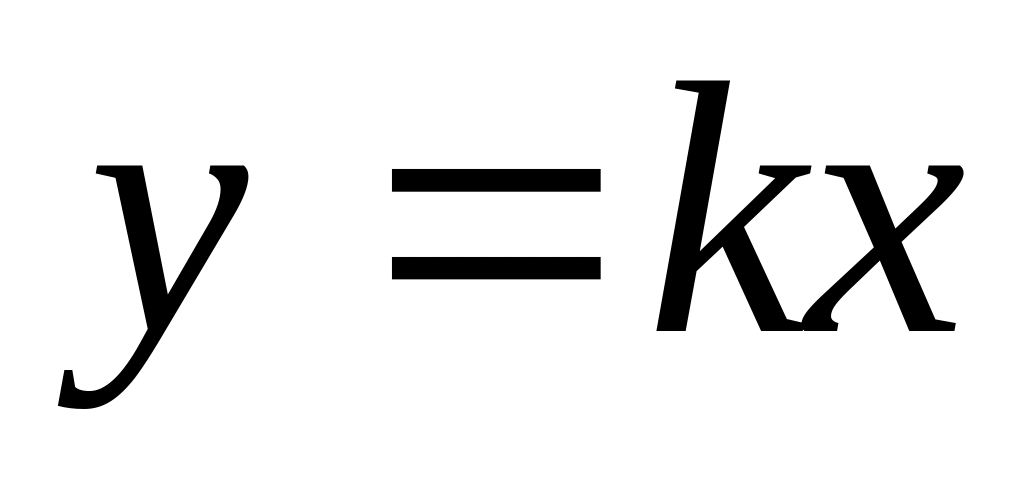 – прямая проходит через начало
координат;
– прямая проходит через начало
координат;
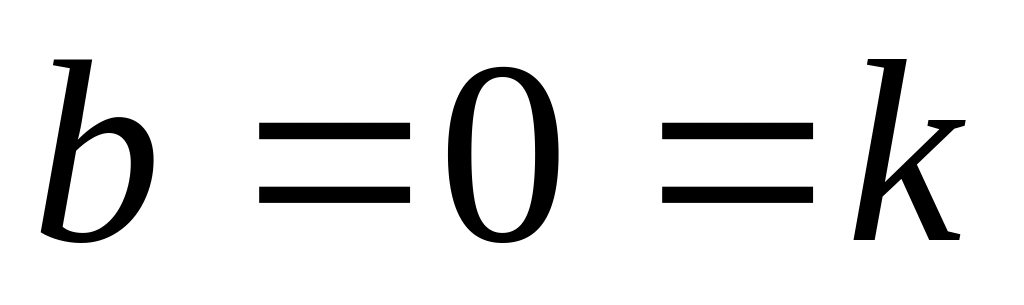 ,
,
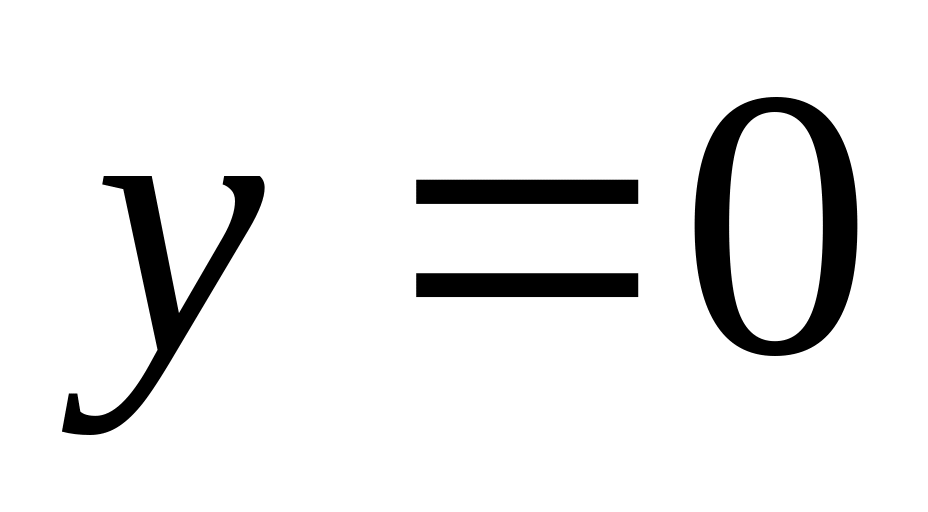 – уравнение оси Ox;
– уравнение оси Ox;
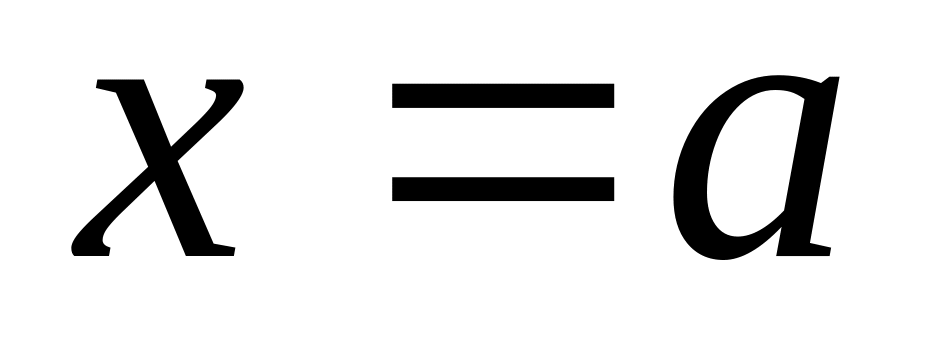 – уравнение
прямой, параллельной оси Oy
и отстоящей от нее на
;
– уравнение
прямой, параллельной оси Oy
и отстоящей от нее на
;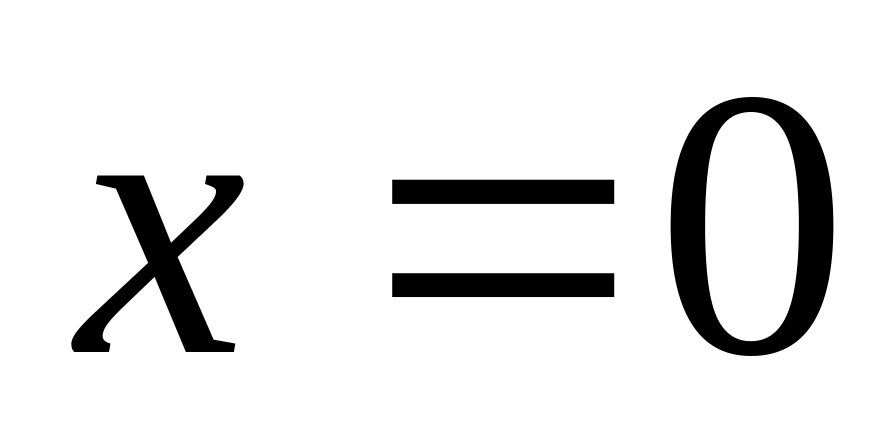 – уравнение
оси Oy;
– уравнение
оси Oy;
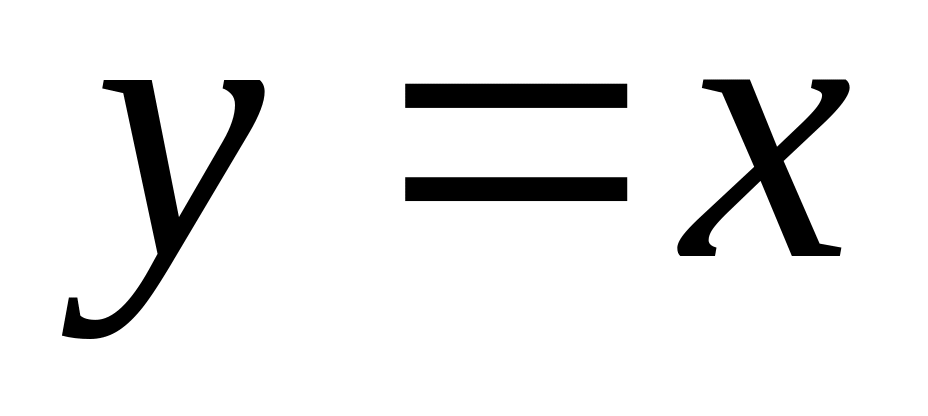 – уравнение
биссектрисы I
и III
координатных углов;
– уравнение
биссектрисы I
и III
координатных углов;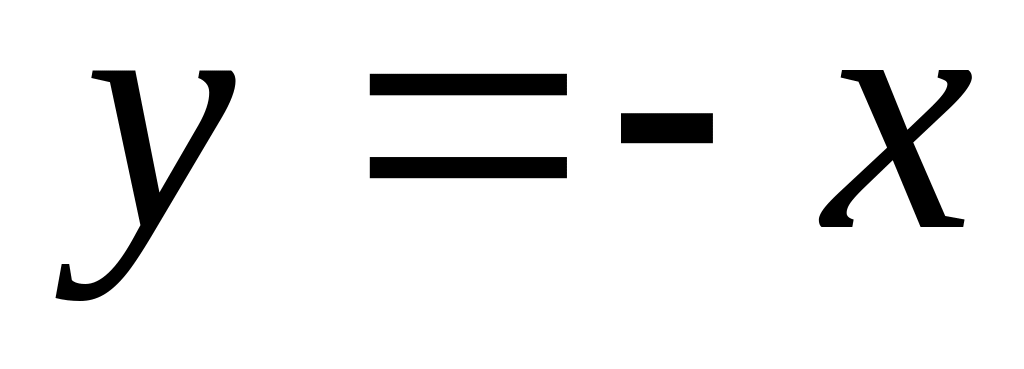 – уравнение
биссектрисы II
и IV
координатных углов.
– уравнение
биссектрисы II
и IV
координатных углов.
Общее уравнение прямой
Любую
прямую на плоскости можно задать
уравнением:
![]() ,
где
,
,
где
,
![]() и
и
![]() – коэффициенты, одновременно не равные
нулю.
– коэффициенты, одновременно не равные
нулю.
Справедливо утверждение: каждая прямая на плоскости с прямоугольной системой координат определяется уравнением первой степени, и, наоборот, каждое уравнение первой степени определяет некоторую прямую на плоскости.
Рассмотрим каждое из условий:
Пусть дана прямая , в которой
 ,
,
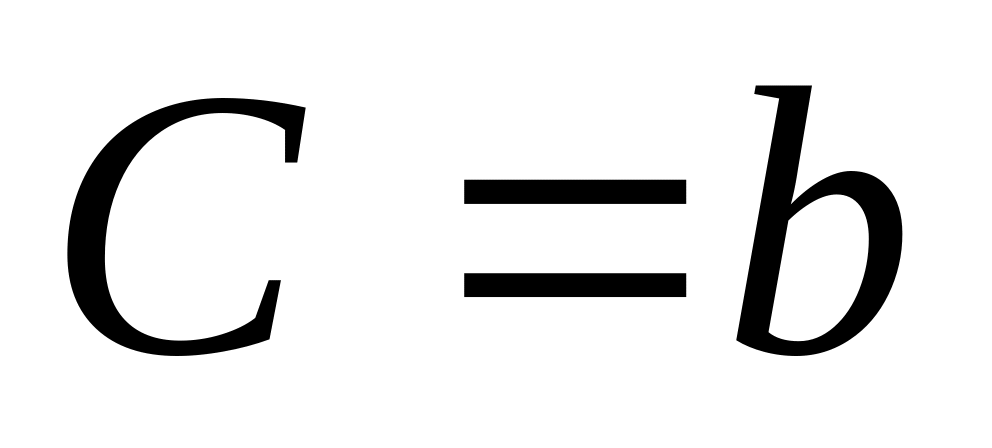 ,
,
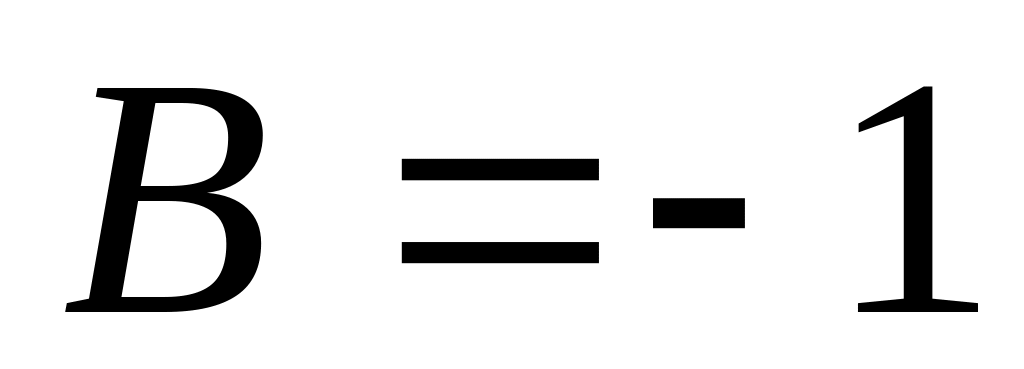 (
(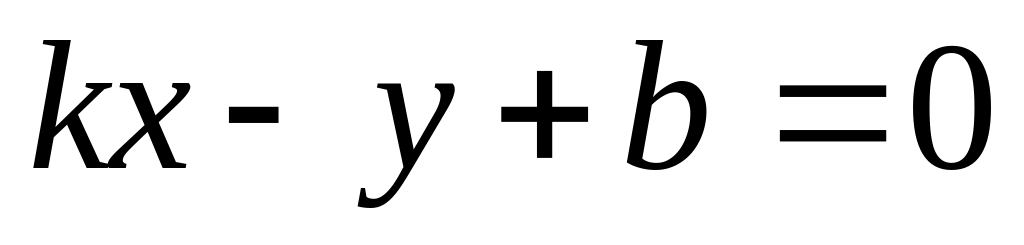 ).
Если
).
Если
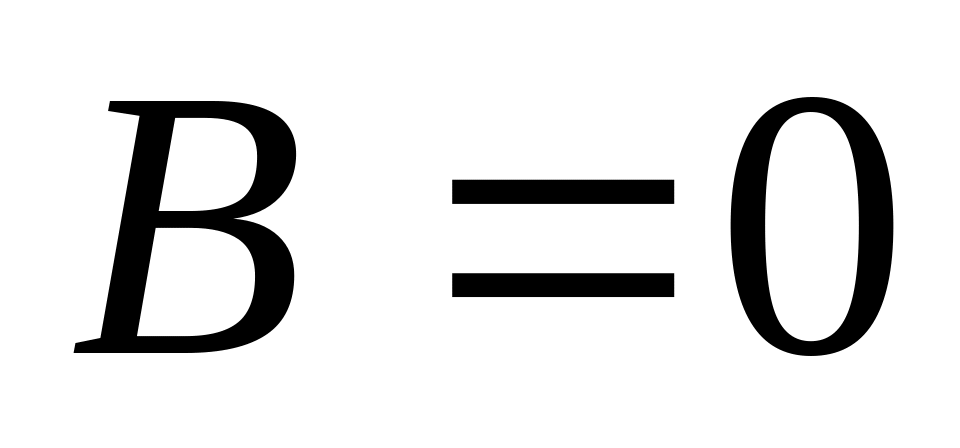 ,
,
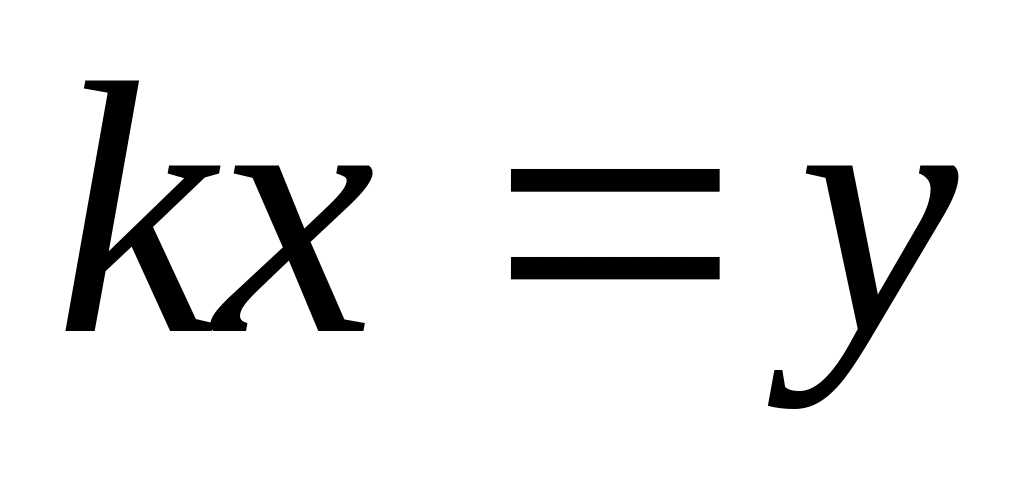 – тоже прямая. Итак, любая прямая –
уравнение первой степени.
– тоже прямая. Итак, любая прямая –
уравнение первой степени.Покажем, что произвольному уравнению первой степени ( , и одновременно не равны 0) соответствует прямая на плоскости.
если
![]() ,
то
,
то
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() .
Значит
– прямая линия. Если
,
.
Значит
– прямая линия. Если
,
![]() ,
то
,
то
![]() – уравнение прямой, параллельной оси
Oy.
Уравнение
– общее
уравнение прямой.
– уравнение прямой, параллельной оси
Oy.
Уравнение
– общее
уравнение прямой.
Уравнение прямой в отрезках
П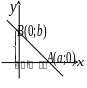 усть
дана прямая
.
Если
усть
дана прямая
.
Если
![]() ,
то, разделив на
,
то, разделив на
![]() .
Имеем:
.
Имеем:
![]() ,
или
,
или
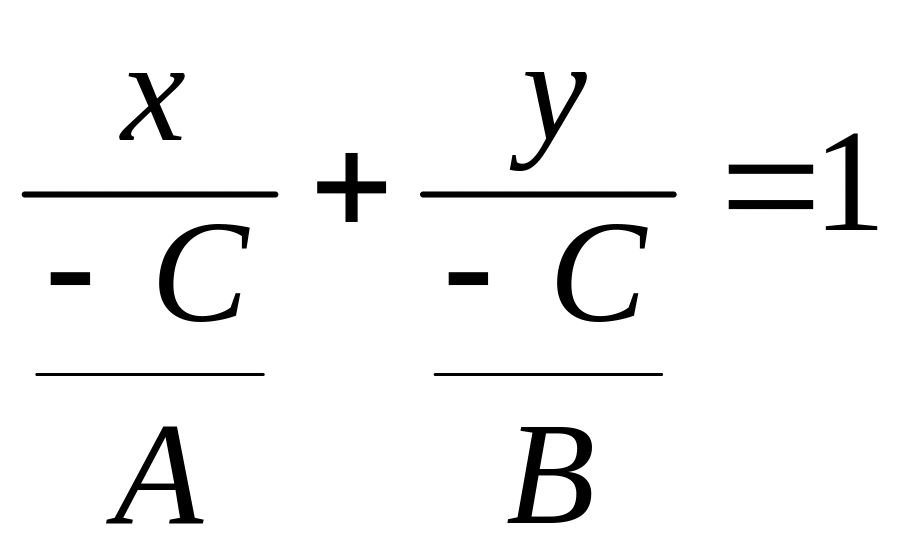 .
Обозначив
.
Обозначив
![]() ,
,
![]() ,
получим
,
получим
![]() – уравнение
прямой в отрезках;
и
– отрезки, которые она отсекает на осях
координат.
– уравнение
прямой в отрезках;
и
– отрезки, которые она отсекает на осях
координат.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть
дана точка
![]() .
Выведем уравнение прямой, проходящей
через нее и имеющей угловой коэффициент
.
Искомое уравнение должно иметь вид
,
но т.к. прямая проходит через
.
Выведем уравнение прямой, проходящей
через нее и имеющей угловой коэффициент
.
Искомое уравнение должно иметь вид
,
но т.к. прямая проходит через
![]() ,
то ее координаты удовлетворяют данному
уравнению:
,
то ее координаты удовлетворяют данному
уравнению:
![]() .
Если мы из первого уравнения вычтем
почленно второе, то
.
Если мы из первого уравнения вычтем
почленно второе, то
![]()
![]() .
Это и есть искомое уравнение:
.
Это и есть искомое уравнение:
![]() ;
;
![]() .
.
