2. Пустое множество

Множество, не имеющее ни одного элемента, называют пустым множеством. Примерами могут служить:

1. множество точек пересечения двух параллельных прямых;

2. множество треугольников, сумма внутренних углов которых отлична от 180°;

3. множество квадратных уравнений, имеющих более двух различных корней;

4. множество решений системы уравнений

5. множество прямоугольных треугольников, у которых сумма квадратов катетов не равна квадрату гипотенузы;

6. множество шестиногих собак.

Фактически во всех этих примерах речь идет об одном и том же множестве: пустое множество единственно – нет разных пустых множеств. Пустое множество обозначается так: Ø.

О некоторых множествах до сих пор неизвестно, пусты они или нет. Например, неизвестно, пусто ли множество цифр, встречающихся лишь конечное число раз в десятичном разложении числа π.

3. Числовые множества

Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, числа, уравнения, точки, углы и т.д. Именно этим объясняется чрезвычайная широта теории множеств и ее приложимость к самым разнообразным областям знания (математика, физика, лингвистика, экономика и т.д.). Для математики особо важную роль играют множества, составленные из "математических" объектов – чисел, геометрических фигур и т.д. Очень часто встречаются числовые множества, т.е. множества, элементами которых являются числа. Примерами числовых множеств являются:

1. множество всех натуральных чисел ( );

2. множество всех положительных рациональных чисел ( );

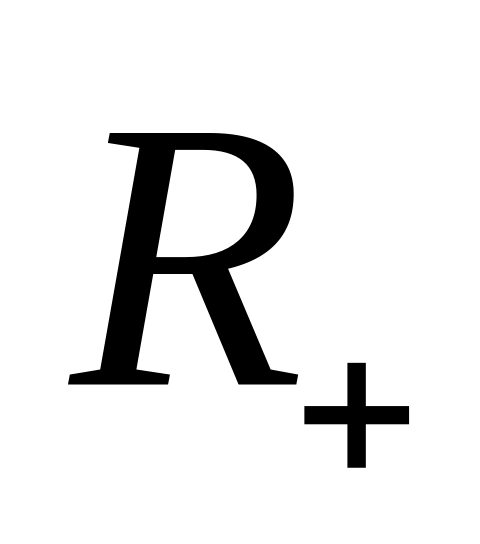3. множество всех рациональных чисел( );

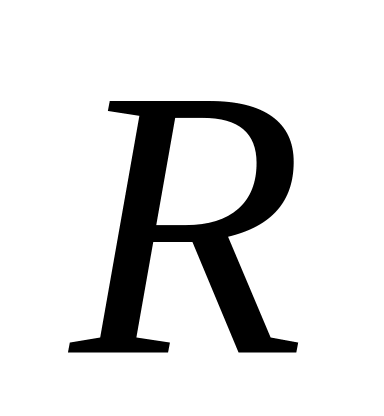4. множество всех целых чисел ( );

5. множество всех чисел, удовлетворяющих неравенству ;

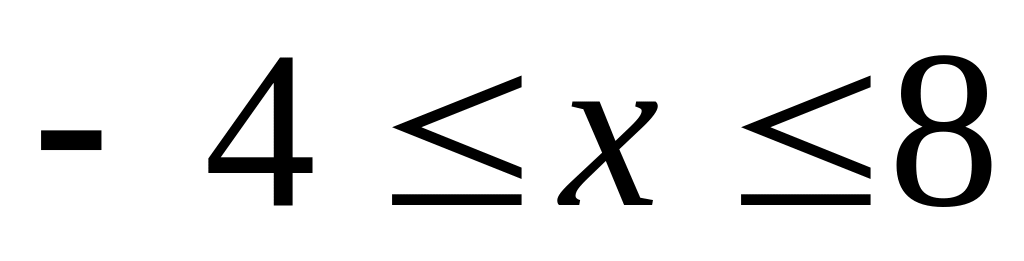6. м ножество всех чисел вида 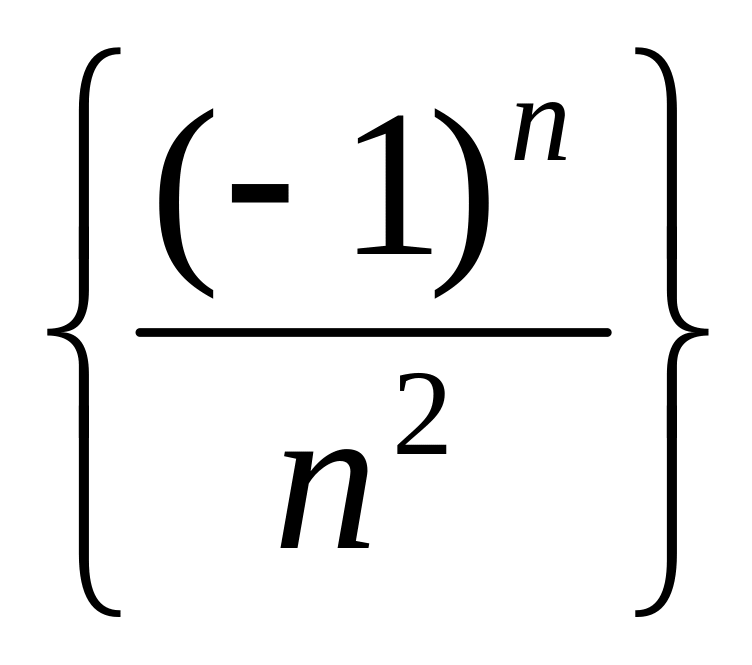, где n принимает все натуральные значения.

Некоторые числовые множества имеют особые названия. Если даны два числа a и b, a<b, то множество всех чисел, удовлетворяющих неравенству , называют числовым отрезком или, если это не вызывает недоразумений, просто отрезком и обозначают [a; b]. На числовой оси ему соответствует отрезок с концами a и b (см. рис. 3).

Множество чисел, удовлетворяющих неравенству , называют числовым промежутком или, короче, промежутком и обозначают (a, b). На числовой оси это множество изображается отрезком, у которого отброшены концевые точки (см. рис. 4).

Иногда нам будут встречаться множества чисел, удовлетворяющих неравенствам или (рис. 5). Их называют (числовыми) полуотрезками и обозначают [a; b), или (a; b]. Квадратная скобка означает, что соответствующий конец включается в множество, а круглая, что он исключается.

Числовые отрезки, полуотрезки и промежутки имеют конечную длину. Рассмотрим теперь множество чисел, удовлетворяющих неравенству +∞. Такое множество называется числовым лучом. Числовой луч имеет бесконечную длину. Числовым лучом называют и множество чисел, удовлетворяющее неравенству вида –∞ .

Числовые лучи обозначают так: [a; +∞), (–∞;a].

С числовыми множествами приходится иметь дело при решении уравнений и неравенств. С каждым уравнением связаны два числовых множества. Первое из них – область определения уравнения. Это множество состоит из всех значений x, для которых имеют смысл обе части уравнения. Например, область определения уравнения

задается условиями (квадратный корень в множестве действительных чисел можно извлечь лишь из неотрицательного числа) и (на нуль делить нельзя). Отсюда получаем, что область определения данного уравнения состоит из всех точек числового отрезка [-5, 5], кроме точки x=2.

Второе множество, связываемое с уравнением, – это множество его корней, т.е. чисел, при подстановке которых в уравнение оно обращается в тождество.

Например, для данного уравнения множество корней состоит из одного числа 3.