
- •1. Аксиоматика 3
- •2. Множества 4
- •3. Аналитическая геометрия 14
- •4. Векторная алгебра 25
- •5. Матрицы и определители 30
- •Аксиоматика
- •Аксиоматический метод построения математики
- •Математический язык
- •Множества
- •Понятие множества
- •Пустое множество
- •Числовые множества
- •Подмножества
- •Пересечение множеств
- •Объединение множеств
- •Вычитание множеств
- •Аналитическая геометрия
- •Система координат на плоскости и в пространстве
- •Расстояние между двумя точками на плоскости
- •Уравнение линии. Уравнение прямой с угловым коэффициентом
- •Уравнение – уравнение прямой с угловым коэффициентом k
- •Общее уравнение прямой
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой, проходящей через данную точку
- •Уравнение прямой, проходящей через две данные (различные) точки и
- •Полярные координаты
- •Угол между прямыми
- •Уравнение окружности
- •Эллипс. Каноническое уравнение эллипса
- •Гипербола. Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение параболы
- •У равнение сферы
- •Векторная алгебра
- •Понятие вектора
- •Коллинеарные векторы
- •Операции над векторами
- •Угол между векторами
- •Проекция вектора на ось
- •Скалярное произведение двух векторов
- •Координаты вектора
- •Разложение векторов
- •Действия над векторами, заданным координатами в пространстве
- •Матрицы и определители
- •Матрицы
- •Определители
- •Определители третьего порядка
- •Миноры и алгебраические дополнения матрицы
- •Обратная матрица
- •Системы линейных уравнений
- •Формулы Крамера
- •Матричный способ решения систем линейных уравнений
- •Метод Гаусса
- •Функции
- •Понятие функции
- •Способы задания функции
- •Обзор элементарных функций и их графиков
- •Пределы
- •Предел последовательности
- •Предел функции
- •Непрерывность функции
- •Производная
- •Определение производной
- •Правила дифференцирования
- •Производные высших порядков
- •Применение производной для исследования функции
- •Неопределенный интеграл
- •Способы интегрирования
- •О пределенный интеграл
- •Дифференциальные уравнения
- •Основные понятия:
- •Признаки сходимости ряда:
- •Ряды по степени разности
- •Теория вероятностей
- •Основные понятия теории вероятностей
- •Классическое определение вероятности
- •Геометрические вероятности
- •Алгебра событий
- •Теорема сложения вероятностей двух несовместимых событий
- •Теорема умножения вероятностей.
- •Теорема сложения вероятностей совместимых событий
- •Формула полной вероятности
- •Теорема умножения вероятностей независимых событий:
- •Дискретные случайные величины
- •Закон распределения дискретных случайных величин
- •Функция распределения случайной величины
- •Нормальное распределение
- •Числовые характеристики случайных величин
- •Свойства математического ожидания (мо) дискретной случайной величины:
- •Дисперсия дискретной случайной величины
- •Среднее квадратичное отклонение (стандартное)
- •Системы двух случайных величин и их числовые характеристики
- •Литература
Теорема умножения вероятностей независимых событий:
Если
события
![]() независимы, то вероятность их произведения
равна произведению вероятностей этих
событий:
независимы, то вероятность их произведения
равна произведению вероятностей этих
событий:
![]()
Вычисление
вероятности суммы независимых событий:
![]() где
где
![]() .
Если независимые события
имеют одинаковую вероятность, равную
,
то вероятность появления хотя бы одного
из этих событий выражается функцией
.
Если независимые события
имеют одинаковую вероятность, равную
,
то вероятность появления хотя бы одного
из этих событий выражается функцией
![]() ,
где
,
где
![]() .
.
Дискретные случайные величины
Определение 1. Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.
Случайные
величины обозначаются прописными
буквами
![]() ,
а их возможные значения – соответственно
строчными
,
а их возможные значения – соответственно
строчными
![]() .
.
Определение 2. Дискретной случайной величиной называется величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности.
Определение 3. Непрерывной случайной величиной называется случайная величина, которая может принимать все значения от некоторого промежутка.
Определение
4. Под
суммой (произведением) случайных
величин![]() понимают
случайную величину
понимают
случайную величину
![]()
![]() возможные значения которой состоят из
суммы (произведения) каждого возможного
значения величины X
и каждого возможного значения величины
Y.
возможные значения которой состоят из
суммы (произведения) каждого возможного
значения величины X
и каждого возможного значения величины
Y.
Закон распределения дискретных случайных величин
Величина Х считается заданной, если перечислены все ее возможные значения, а также вероятности, с которым величина Х может принимать эти значения. Указанный перечень всех ее возможных значений и их вероятностей называется законом распределения дискретной случайной величины. Он может иметь вид таблицы:
|
|
|
|
… |
|
|
|
|
|
… |
|
Таблица
читается следующим образом: случайная
величина
может принимать значения
![]() с вероятность
с вероятность
![]() .
.
Т.к.
принимает всегда одно из значений, то
![]() .
.
Пример: в лотерее разыгрывается 10000 билетов. Выигрышными являются 1 билет в 1000 рублей, 10 выигрышей по 100 рублей, и 100 выигрышей по 1 рубль. Найти закон распределения случайного выигрыша для владельца одного лотерейного билета.
|
0 |
1 |
100 |
1000 |
|
0,9889 |
0,01 |
0,001 |
0,0001 |
![]()
Функция распределения случайной величины
Функцией
распределения (интегральной функцией)
случайной величины
![]() называется функция
называется функция
![]() действительной переменной
действительной переменной
![]() ,
определяемая равенством:
,
определяемая равенством:
![]() ,
где
,
где
![]() – вероятность того, что случайная
величина
принимает значение меньшее
.
Вероятность того, что случайная величина
примет значение из полуинтервала
– вероятность того, что случайная
величина
принимает значение меньшее
.
Вероятность того, что случайная величина
примет значение из полуинтервала
![]() ,
равна разности значений ее функции
распределения в концах этого промежутка
,
равна разности значений ее функции
распределения в концах этого промежутка
![]() .
.
Свойства функции распределения:
Все значения функции распределения принадлежат отрезку
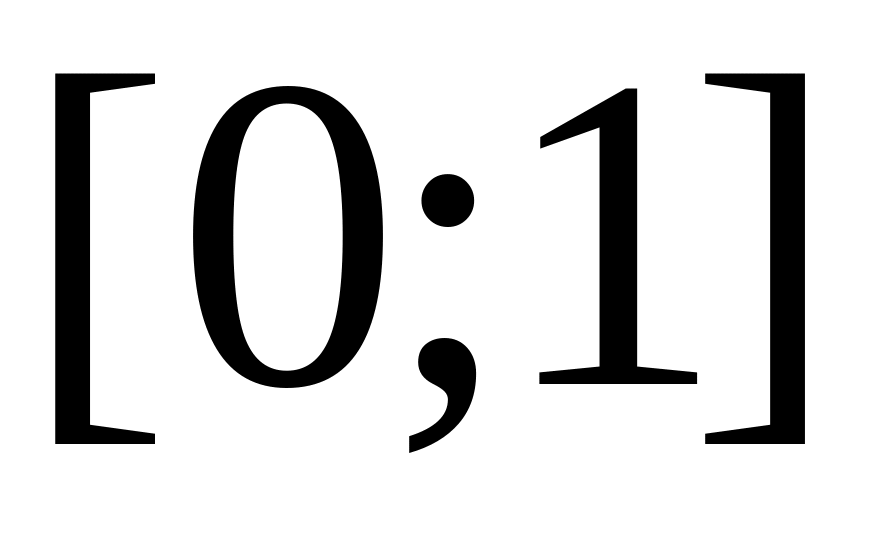 ,
т.е.
,
т.е.
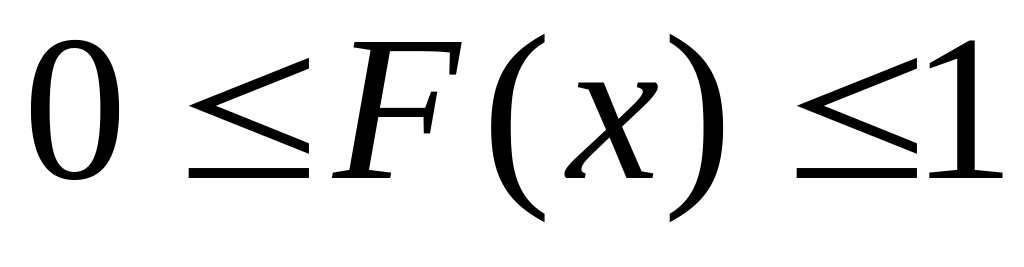 .
Это следует из определения функции
распределения и свойств вероятности.
.
Это следует из определения функции
распределения и свойств вероятности.
Функция распределения является неубывающей, т.е. если
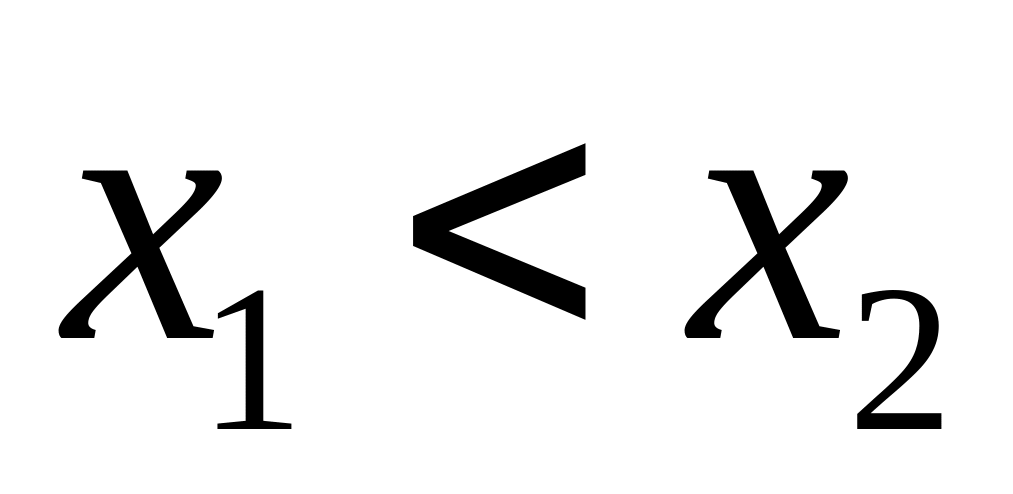 ,
то
,
то
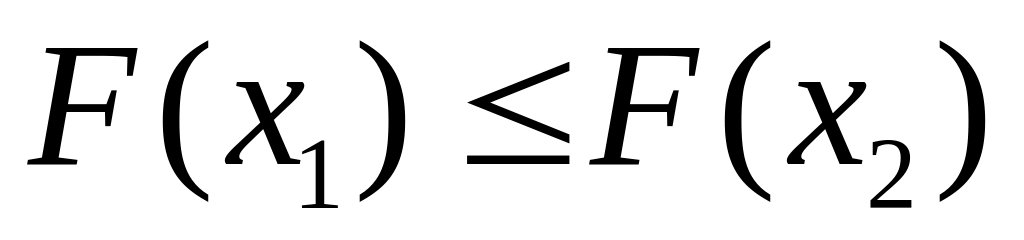 .
.Функция в точке непрерывна слева, т.е.
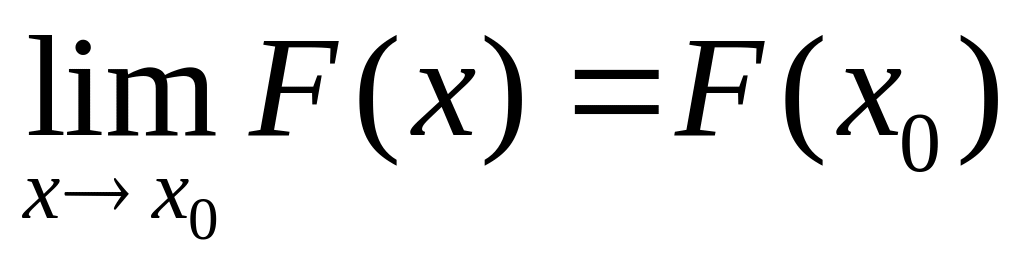 при любом
.
при любом
.Вероятность того, что непрерывная случайная величина примет какое-либо заранее заданное значение, равна нулю:
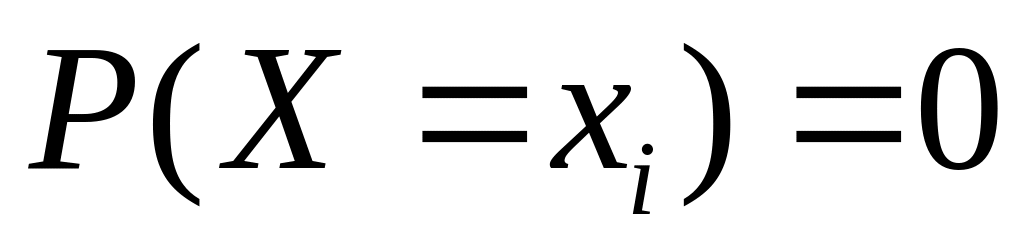 .
.Если возможные значение случайной величины принадлежат интервалу
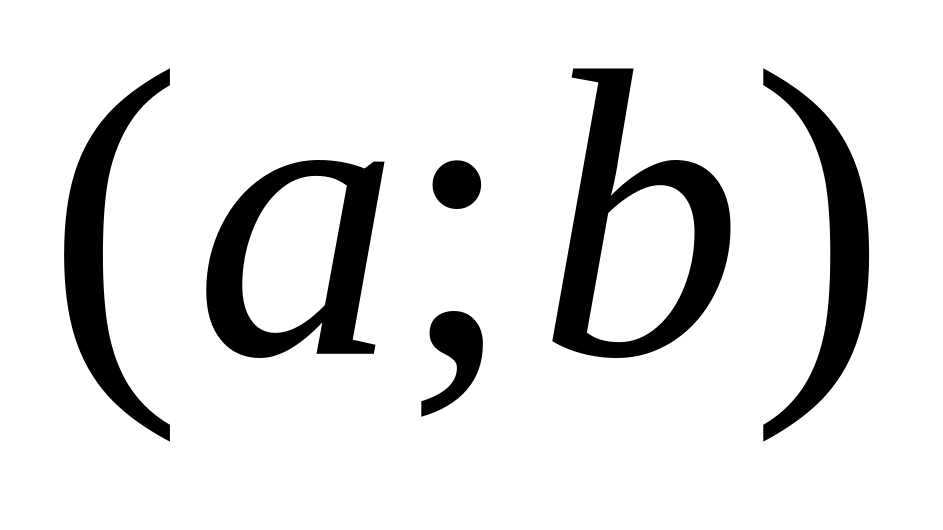 то:
то:
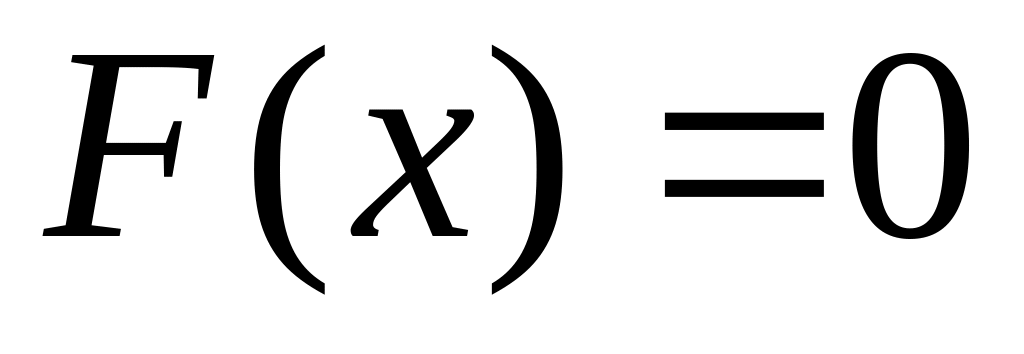 при
при
 ;
;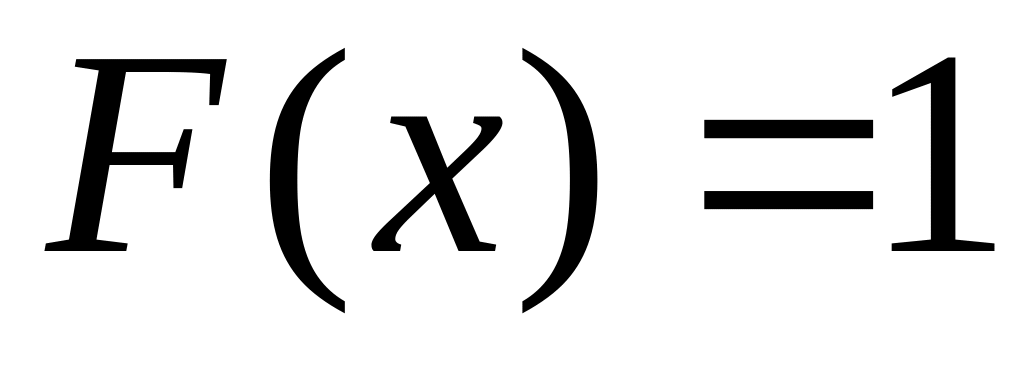 при
при
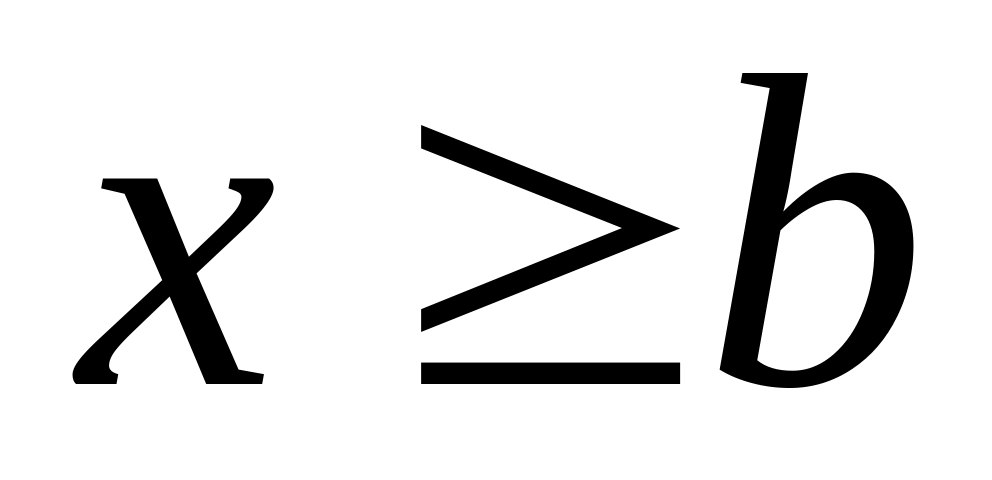 .
.
Следствие:
если возможные значения непрерывной
случайной величины расположены на всей
числовой оси, то справедливы следующие
предельные соотношения:
![]() ;
;
![]() .
.
Г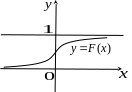 рафик
функции распределения целиком расположен
в полосе между прямыми
рафик
функции распределения целиком расположен
в полосе между прямыми
![]() и
и
![]() .
.
Плотностью
распределения вероятностей непрерывной
случайной величины
(дифференциальной функцией распределения)
называется функция
![]() ,
равная производной интегральной функции
распределения:
,
равная производной интегральной функции
распределения:
![]() .
График функции
называется кривой распределения.
.
График функции
называется кривой распределения.
Вероятностью
попадании
непрерывной случайной величины
в интервал
равна определенному интегралу от ее
плотности вероятности, взятому в
пределах от
![]() до
до
![]() :
:
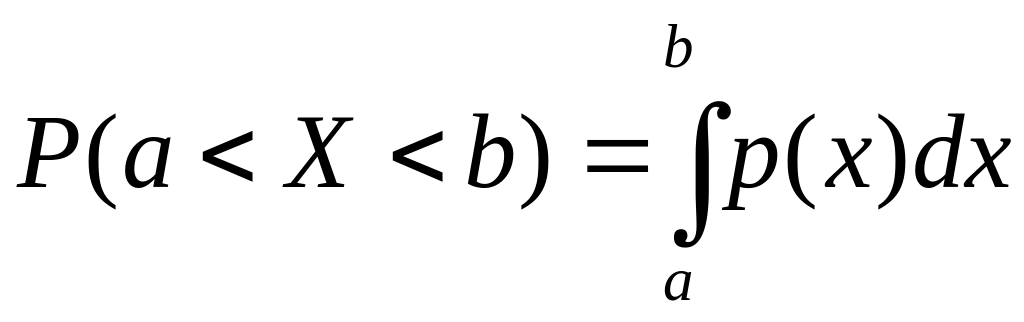 .
.
Распределение
вероятностей непрерывной случайной
величины
,
принимающей все свои значения на отрезке
![]() ,
называется
равномерным,
если ее плотность вероятности
на этом отрезке постоянна, а вне его
равна нулю, т.е.
,
называется
равномерным,
если ее плотность вероятности
на этом отрезке постоянна, а вне его
равна нулю, т.е.
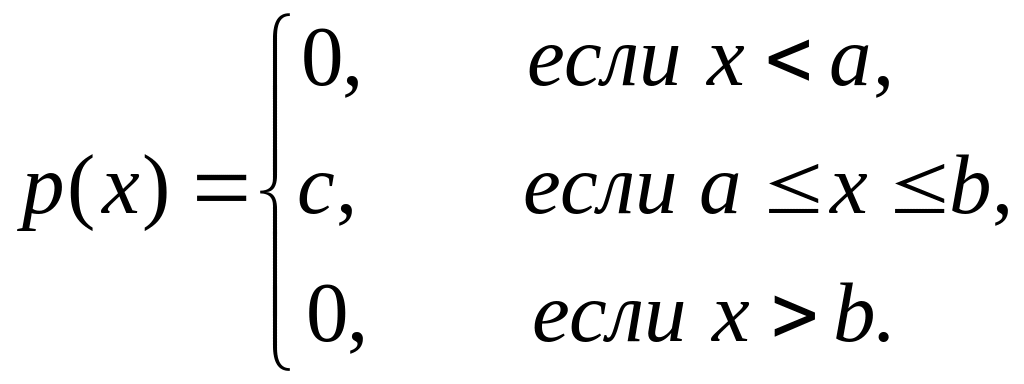
О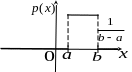 тсюда
тсюда
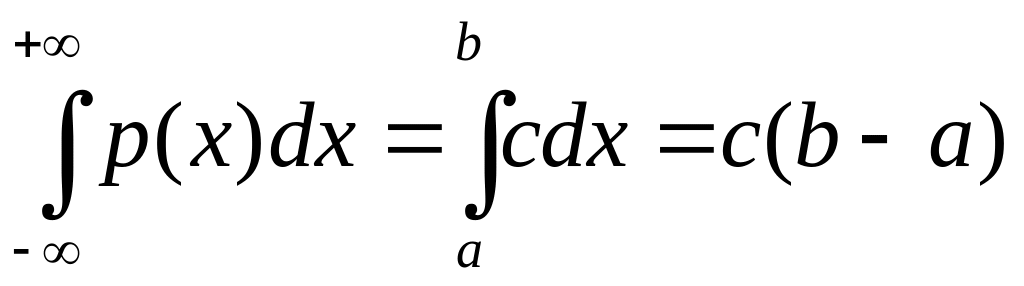 .
Но
.
Но
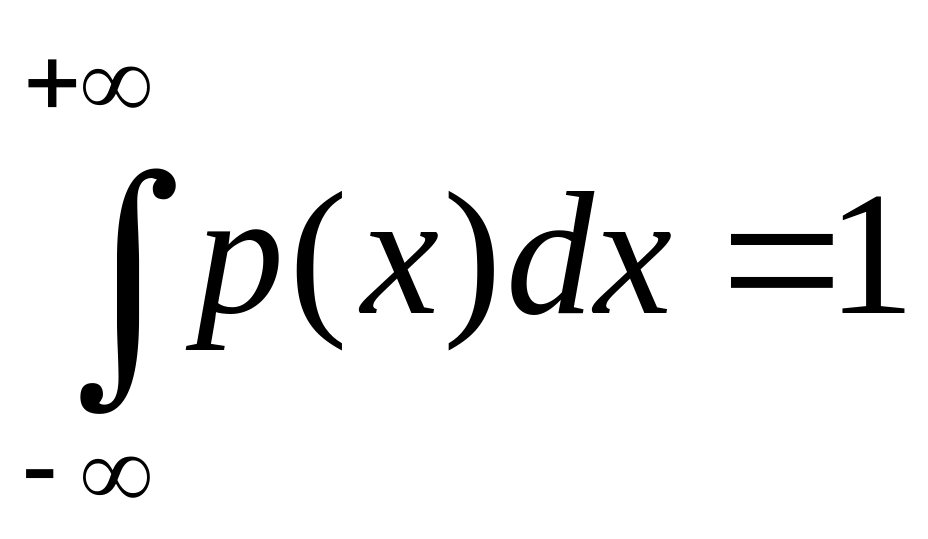 .
Значит
.
Значит
![]() ,
откуда
,
откуда
![]() .
.
График функции имеет вид:
Определим
интегральную функцию распределения
:
если![]() ,
то
,
то
![]() и, следовательно
.
Если
и, следовательно
.
Если
![]() ,
то
,
то
![]() и
и
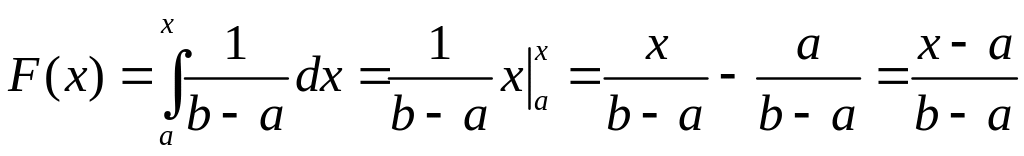 .
Если
.
Если
![]() ,
то
и
,
то
и
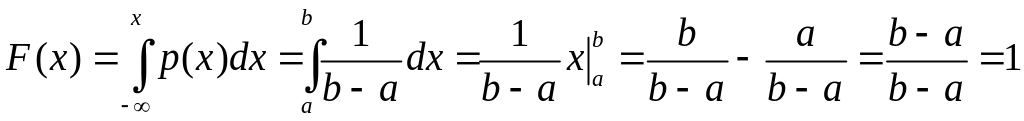 .
.
Г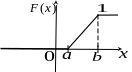 рафик
функции
имеет вид:
рафик
функции
имеет вид:
