
- •Кафедра информатики и прикладной математики математика
- •Часть 2
- •Теория вероятностей и элементы математической статистики учебно - методический комплекс
- •Санкт-Петербург
- •Информация о дисциплине
- •1.1. Предисловие
- •Содержание дисциплины и виды учебной работы Объем дисциплины и виды учебной работы
- •Перечень видов практических занятий и контроля:
- •2. Рабочие учебные материалы
- •2.1. Рабочая программа (объем 150 часов) Введение
- •Раздел 1. Случайные события (50 часов)
- •Раздел 2. Случайные величины ( 60 часов)
- •Раздел 3. Элементы математической статистики (40 часов)
- •2.2. Тематический план занятий Тематический план дисциплины
- •Тематический план дисциплины для студентов очно-заочной формы обучения
- •Тематический план дисциплины для студентов заочной формы обучения
- •2.3. Структурно-логическая схема дисциплины Математика ч.2. Теория вероятностей и элементы математической статистики Теория
- •Раздел 1 Случайные события Раздел 3 Элементы математической Статистики
- •Раздел 2 Случайные величины
- •2.4. Временной график изучения дисциплины
- •2.5. Практический блок Практические занятия (очно-заочная форма обучения)
- •Практические занятия (заочная формы обучения)
- •Практические занятия (очная форма обучения)
- •Лабораторные работы (очно-заочная форма обучения)
- •Лабораторные работы (очная форма обучения)
- •Лабораторные работы (заочная форма обучения)
- •2.6. Бально-рейтинговая система
- •Информационные ресурсы дисциплины
- •Библиографический список Основной:
- •3.2. Опорный конспект по курсу “ Математика ч.2. Теория вероятностей и элементы математической статистики” введение
- •Раздел 1. Случайные события
- •1.1. Понятие случайного события
- •1.1.1. Сведения из теории множеств
- •1.1.2. Пространство элементарных событий
- •1.1.3. Классификация событий
- •1.1.4. Сумма и произведение событий
- •1.2. Вероятности случайных событий.
- •1.2.1. Относительная частота события, аксиомы теории вероятностей. Классическое определение вероятности
- •1.2.2. Геометрическое определение вероятности
- •Вычисление вероятности события через элементы комбинаторного анализа
- •1.2.4. Свойства вероятностей событий
- •1.2.5. Независимые события
- •1.2.6. Расчет вероятности безотказной работы прибора
- •Формулы для вычисления вероятности событий
- •1.3.1. Последовательность независимых испытаний (схема Бернулли)
- •1.3.2. Условная вероятность события
- •Вероятность произведения событий
- •1.3.4. Формула полной вероятности и формула Байеса
- •Раздел 2. Случайные величины
- •2.1. Описание случайных величин
- •2.1.1. Определение и способы задания случайной величины Одним из основных понятий теории вероятности является понятие случайной величины. Рассмотрим некоторые примеры случайных величин:
- •2.1.2. Дискретные случайные величины
- •Рассмотрим события Ai , содержащие все элементарные события , приводящие к значению XI:
- •Пусть pi обозначает вероятность события Ai :
- •2.1.3. Непрерывные случайные величины
- •2.1.4. Функция распределения и ее свойства
- •2.1.5. Плотность распределения вероятности и ее свойства
- •2.2. Числовые характеристики случайных величин
- •2.2.1. Математическое ожидание случайной величины
- •2.2.2. Дисперсия случайной величины
- •2.2.3. Нормальное распределение случайной величины
- •2.2.4. Биномиальное распределение
- •2.2.5. Распределение Пуассона
- •Раздел 3. Элементы математической статистики
- •3.1. Основные определения
- •Систематизация выборки
- •Гистограмма
- •3.3. Точечные оценки параметров распределения
- •Основные понятия
- •Точечные оценки математического ожидания и дисперсии
- •3.4. Интервальные- оценки
- •Понятие интервальной оценки
- •Построение интервальных оценок
- •Основные статистические распределения
- •Интервальные оценки математического ожидания нормального распределения
- •Интервальная оценка дисперсии нормального распределения
- •4. Методические указания к выполнению лабораторных работ
- •Выполнение лабораторных работ в ms Excel
- •Лабораторная работа 1 статистическое оценивание параметров распределения
- •Порядок выполнения лабораторной работы
- •Лабораторная работа 2 проверка гипотезы о законе распределения. Критерий пирсона
- •Понятие статистической гипотезы о виде распределения
- •Порядок выполнения лабораторной работы
- •Ячейка Значение Ячейка Значение
- •5. Методические указания к выполнению контрольной работы Задание на контрольную работу
- •Методические указания к выполнению контрольной работы События и их вероятности
- •Случайные величины
- •Среднее квадратическое отклонение
- •Элементы математической статистики
- •6. Блок контроля освоения дисциплины Репетиционные вопросы Тест № 1
- •Вопрос 10
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16
- •Вопрос 17
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Тест № 2
- •Вопрос 1
- •Вопрос 7
- •Вопросы для экзамена по курсу «Теория вероятностей и элементы математической статистики»
- •Глоссарий
- •Продолжение таблицы в
- •Окончание таблицы в
- •Равномерно распределенные случайные числа
- •Содержание
- •Раздел 1. Случайные события………………………………………. 18
- •Раздел 2 . Случайные величины ..………………………… ….. 42
- •Раздел 3. Элементы математической статистики ............... 65
- •4. Методические указания к выполнению лабораторных
- •5. Методические указания к выполнению контрольной
Основные статистические распределения
Построение разного рода оценок и статистических критериев часто основывается на использовании ряда специальных распределений случайных величин.
Нормальное
распределение. Случайная
величина
![]() имеет нормальное распределение с
параметрами
и
имеет нормальное распределение с
параметрами
и
![]() ,
что обозначается как
,
что обозначается как
![]() ,
если плотность вероятности этой случайной
величины имеет вид
,
если плотность вероятности этой случайной
величины имеет вид
![]() .
(3 .25)
.
(3 .25)
График плотности
вероятности случайной величины, имеющей
нормальное распределение, представлен
на рисунке 3.5, на котором видно, что
максимум функции находится в точке
![]() .
.
Поскольку нормальное распределение подробно изучается в курсе теории вероятностей, напомним свойства нормальной случайной величины, которые будут использоваться в дальнейшем.
Р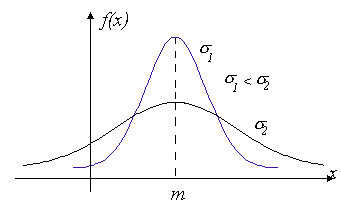 ис.
3.5
ис.
3.5
1)
![]() ,
,
![]() .
.
2) Случайная величина называется центрированной, если ее математическое ожидание равно нулю. Для того чтобы центрировать случайную величину, надо вычесть из нее математическое ожидание:
![]() .
.
Случайная величина называется нормированной, если ее дисперсия равна единице, а математическое ожидание равно нулю.
Для того чтобы нормировать случайную величину, надо ее поделить на среднее квадратическое отклонение:
![]() .
.
Центрированная и нормированная нормальная случайная величина называется стандартной. Таким образом, стандартной будет случайная величина
![]() ~
~
![]() .
(3.26)
.
(3.26)
Вероятность попадания случайной величины в интервал (α,β) вычисляется по формуле
![]() , (3.27)
, (3.27)
где
![]() - интеграл вероятности, представляющий
собой функцию распределения стандартной
нормально распределенной случайной
величины. Интеграл вероятности
табулирован. Его значения приведены в
таблице В Приложения.
- интеграл вероятности, представляющий
собой функцию распределения стандартной
нормально распределенной случайной
величины. Интеграл вероятности
табулирован. Его значения приведены в
таблице В Приложения.
Для стандартной нормальной случайной величины и симметричного промежутка формула (3.27) принимает следующий вид:
![]() .
(3.28)
.
(3.28)
Распределение
![]() (хи-квадрат). Если
(хи-квадрат). Если
![]() ,
,
![]() независимые стандартные нормальные
случайные величины, то говорят, что
случайная величина
независимые стандартные нормальные
случайные величины, то говорят, что
случайная величина
![]() (3.29)
(3.29)
имеет распределение
хи-квадрат с
степенями свободы, что обозначается
как
![]() .
Графики плотности вероятности для
двух значений степени свободы приведены
на рис.3.6.
.
Графики плотности вероятности для
двух значений степени свободы приведены
на рис.3.6.
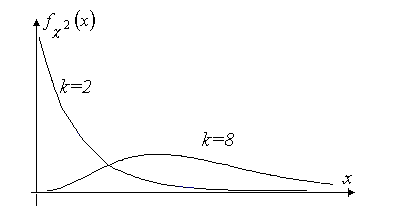 Рис.
3.6
Рис.
3.6
С увеличением
числа степеней свободы
плотность вероятности стремится к
нормальной. При
![]() плотность вероятности постоянно убывает,
а при
плотность вероятности постоянно убывает,
а при
![]() имеет единственный максимум
имеет единственный максимум
![]() ,
,
![]() ,
,
![]() .
.
Распределение
Стьюдента. Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() - независимые стандартные нормальные
случайные величины. Тогда случайная
величина
- независимые стандартные нормальные
случайные величины. Тогда случайная
величина
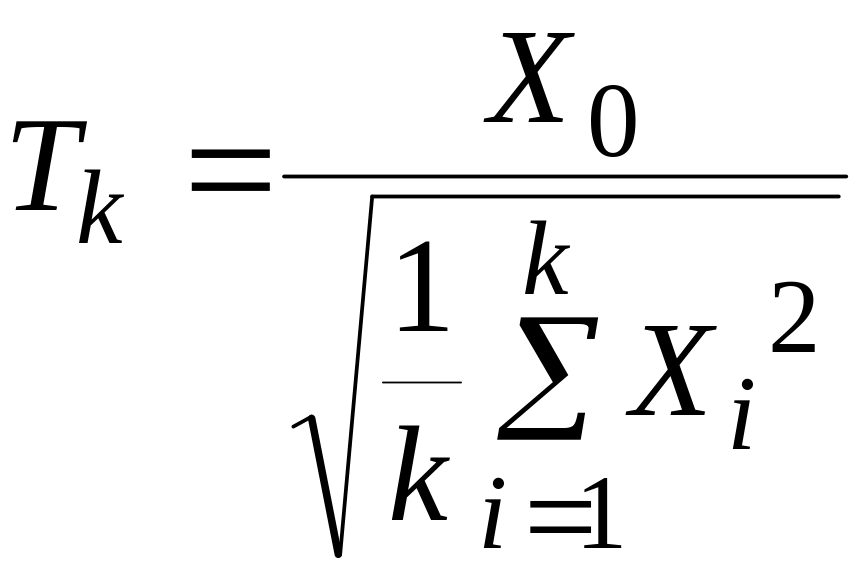 (3.30)
(3.30)
имеет распределение
Стьюдента с
степенями свободы, что обозначается
как
![]() ,
при этом
,
при этом
![]() ,
,
![]() .
.
На рис.3.7 приведены кривые стандартного нормального распределения (кривая 1) и плотности распределения Стьюдента (кривая 2).
Р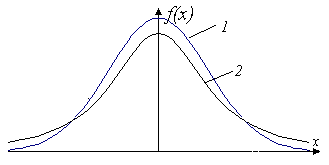 ис.
3.7
ис.
3.7
При плотность распределения Стьюдента стремится к плотности стандартной нормальной случайной величины.
На практике, как
правило, используется не плотность
вероятности, а квантиль распределения.
Напомним, что квантилью порядка (или
уровня)
![]() непрерывной случайной величины
называется такое ее значение
непрерывной случайной величины
называется такое ее значение
![]() ,
которое удовлетворяет равенству
,
которое удовлетворяет равенству
![]()
![]() ,
,
где
![]() - функция распределения, а
- заданное значение вероятности. Рис.3.8
поясняет понятие квантили порядка
.
- функция распределения, а
- заданное значение вероятности. Рис.3.8
поясняет понятие квантили порядка
.
Р ис.
3.8
ис.
3.8
Следующая теорема устанавливает свойства основных выборочных характеристик, вычисленных по выборке, соответствующих нормальному распределению.
Теорема Фишера.
Пусть
- случайная выборка из генеральной
совокупности
![]()
![]() ,
тогда выборочное среднее
,
тогда выборочное среднее
![]() и несмещенная выборочная дисперсия
и несмещенная выборочная дисперсия
![]() независимы, и при этом
независимы, и при этом
1) случайная величина
![]() имеет распределение
имеет распределение
![]() ;
;
2) случайная величина
![]() имеет распределение
имеет распределение
![]() ;
;
3) случайная величина
![]() имеет распределение
имеет распределение
![]() .
.
Доказательство теоремы приведено в [2].
