Глава 7 обчислювальна гідродинаміка

7.1. Поняття про рівняння руху в’язких середовищ

На відміну від попередньо розглянутих задач, наразі йтиметься про дослідження руху в’язких матеріалів при здійсненні ковальсько-штампувальних операцій обробки матеріалів тиском [13]-[14]. Основним інструментом дослідження є скінченнорізницевий підхід.

7.1.1. Рівняння імпульсу в консервативній формі

В якості прикладу задачі обчислювальної гідродинаміки розглянемо задачу рівноканального кутового пресування (РККП) в’язкого матеріалу (пластилін, віск, парафін, полімер) через прямокутний штамп з двома перетинними каналами однакового поперечного перерізу (див. рисунок 7.1).

Для аналізу течії в'язкого середовища в обчислювальній гідродинаміці застосовують рівняння імпульсу або, інакше кажучи, рівняння Нав’є-Стокса [15]-[16]:

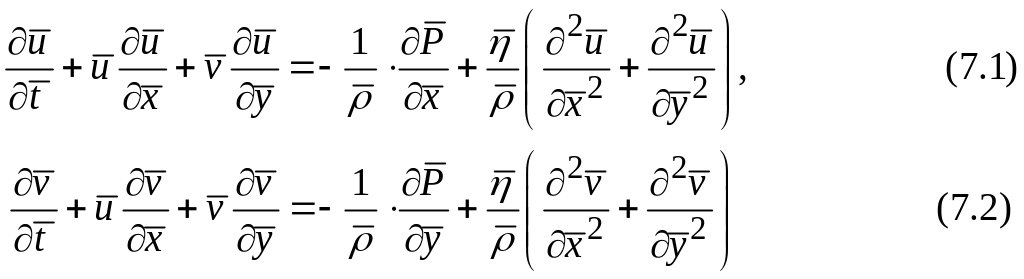
і рівняння нерозривності

, (7.3)

де рискою угорі позначені розмірні величини: , – координати; – час; і – розмірні складові швидкості уздовж осей і відповідно (див. рисунок 7.1); і – густина і в’язкість оброблюваного матеріалу; – тиск пресування.

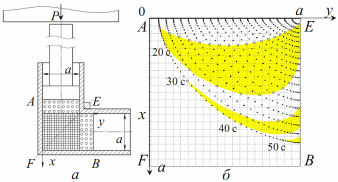
Рисунок 7.1 – (а) Геометрія кутового штампу і (б) розрахункові лінії струму в осередку пластичної деформації AEBF для течії пластиліну

Для створення математичної моделі задачі, зручної для теоретичного аналізу, а також задля забезпечення загальності розв’язків, вводяться наступні безрозмірні величини: , – безрозмірні координати, де характерний розмір – ширина каналу; , – безрозмірні складові швидкості уздовж осей і , де – швидкість матеріалу у вхідному каналі штампу; – безрозмірний тиск, де – густина оброблюваного матеріалу; – число Рейнольдса, де – в’язкість матеріалу моделі; – безрозмірний час; , – безрозмірні координати.

Для випадку, коли після нескладних перетворень рівнянь (7.1), (7.2) одержуємо наступні рівняння імпульсу в консервативній формі:

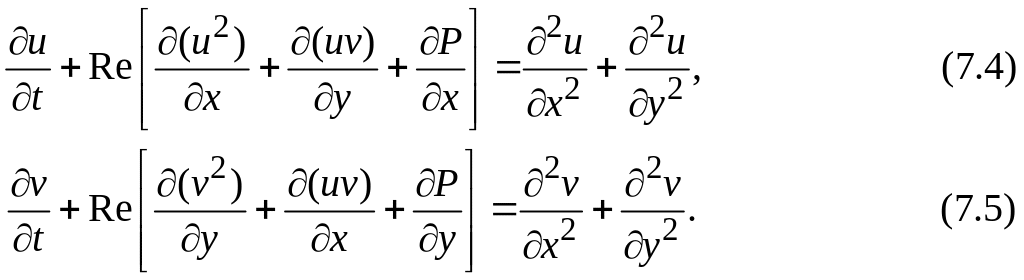
Алгоритм чисельного розв'язку системи рівнянь (7.4)-(7.5) у випадку рівноканального кутового пресування можна проілюструвати наступною блок-схемою (див. рисунок 7.2).

Для розв’язку рівнянь (7.4)–(7.5) застосуємо один із чисельних методів, який знайшов широке розповсюдження при розв’язку задач механіки суцільних середовищ і легко реалізується на комп’ютері – скінченнорізницевим методом. Метод, використовуваний для скінченнорізницевої апроксимації ґрунтується на покриванні області осередку пластичної деформації рівномірною сіткою квадратних елементів (див. рисунок 7.1) з наступною заміною шуканих функцій , і на функції вузлових аргументів. У такий спосіб будується певна система алгебраїчних рівнянь, які являються скінченно-різницевими аналогами рівнянь (7.4)–(7.5), причому одержана система алгебраїчних рівнянь була розв’язана ітераційним методом Річардсона в системі програмування Object Pascal (IDE Lazarus) (див. виконуваний файл Navier-Stokes_u,v,P.exe).

7.1.2 Формулювання початкових і граничних умов

Зазначимо, що завжди для знаходження розв’язку рівнянь в частинних похідних необхідно задавати як початкові, так і граничні умови.

Рисунок 7.2 – Блок-схема алгоритму розв'язання рівнянь Нав’є-Стокса, записаних для змінних компонентів швидкості u, v і тиску P

Так, для знаходження параметрів усталеного режиму початкові умови беруться у вигляді грубого наближення до стаціонарного розв’язку:

, , . (7.6)

Граничні умови для швидкостей формулюються із тих міркувань, що матеріал при РККП тече без прилипання до стінок ( ) і ( ) штампу, тобто швидкість частинки матеріалу уздовж стінок дорівнює дотичній складовій швидкості матеріальної частинки у внутрішньому шарі оброблюваного матеріалу, який прилягає до стінок. При цьому нормальні складові швидкостей в шарах, які прилягають до границі зсередини та «ззовні», однакові і протилежно напрямлені, а на самій стінці штампу нормальна складова швидкості дорівнює нулю.

Отже, для стінки маємо:

; ; . (7.7)

Для стінки :

; ; . (7.8)

Що стосується кутових точок штампу і , то в них із фізичних міркувань приймаються нульові компоненти швидкості (див. рисунок 7.3):

, ; , . (7.9)

Гранична умова для тиску біля стінок із ковзанням формулюється із вимоги рівності тиску в прилеглих вузлах сітки по обидва боки границі штампу. При цьому тиск матеріалу на вихідній поверхні осередку пластичної деформації може бути відсутнім (див. рисунок 7.4):

; ; . (7.10)

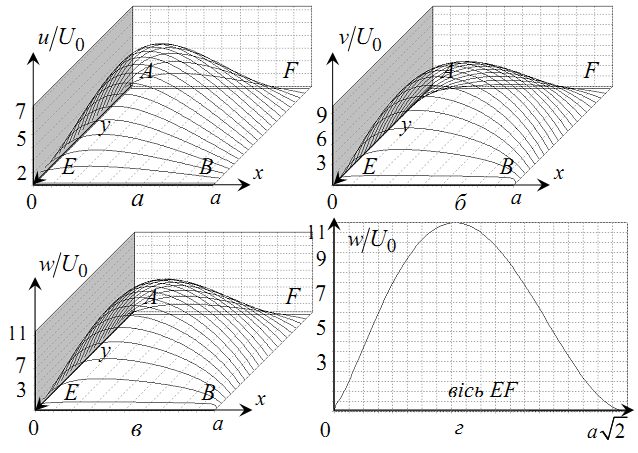
Рисунок 7.3 – Поля складових швидкостей (а)-(в), де вхід – зліва, вихід – до нас; (г)  розподіл швидкості потоку уздовж діагоналі

Із формули Пуазейля одержуємо наступні співвідношення для перепаду розмірного і безрозмірного тиску на кожному кроці координати:

, , (7.11)

де – число комірок сітки уздовж сторони квадрату (див. рисунок 7.1).

Граничні умови для тиску на вході мають вигляд:

. (7.12)

Система рівнянь (7.4)–(7.5) розв’язувалась із початковими (7.6) та граничними (7.7)–(7.10), (7.12) умовами (див. виконуваний файл Navier-Stokes_u,v,P.exe) для течії пластиліну при РККП для наступних числових значень: густина матеріалу  кг/м³, межа текучості  кПа, ширина кожного каналу  мм, швидкість пресування  мм/с, в’язкість плинного матеріалу  кПа•с, число Рейнольдса , питома теплоємність пластиліну  кДж/(кг•К), питома теплопровідність  Дж/(м•с•К), крок часу  пс, кількість кроків координати , кількість кроків часу , час установлення стаціонарного режиму  μс. П’ять ізохрон, позначені кружками на рисунку 7.1, відповідають наступним послідовним моментам часу:  с,  с,  с,  с,  с. Відносна похибка ітерацій становить .

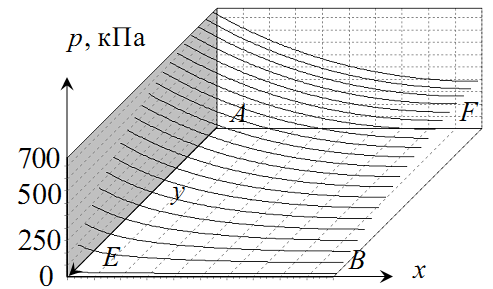
Рисунок 7.4 – Поле тиску , де вхід – зліва, вихід – до нас

Результати чисельного розв’язку рівнянь Нав’є-Стокса для течії пластиліну при РККП представлені на рисунках 7.1б, 7.3–7.5. На рисунку 7.1б показані положення частинок-маркерів через рівні проміжки часу. В початковий момент часу частинки знаходились на вхідному перерізі . Якщо поєднати точки, які відповідають положенням маркерів в послідовні моменти часу, одержимо лінії току. Положення маркерів в моменти часу , , , і зображені кружками. Якщо поєднати маркери, які відповідають моменту часу , одержимо ізохрону і т.д. На рисунку 7.1б виразно спостерігається вільна від маркерів застійна зона, яка прилягає до кута прес-форми. Розв’язок системи рівнянь (7.4)-(7.5) дозволяє дослідити поле повної швидкості потоку (див. рисунок 7.3) і тиску (див. рисунок 7.4) в будь-якій точці досліджуваної області  .

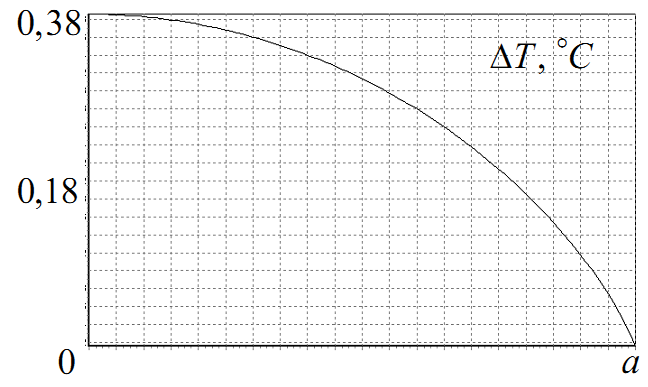
Рисунок 7.5 – Приріст температури в зоні осередку пластичної деформації

Якби шари оброблюваного матеріалу не ковзали один відносно іншого, то швидкість шару була б пропорційною його відстані від точки прес-форми. Проте, як це видно на графіку (див. рисунок 7.3г), де представлена залежність швидкості шару від його відстані від точки уздовж діагоналі , наростання швидкості шару зі збільшенням відстані від точки спочатку сповільнюється, а потім швидкість шарів істотно зменшується. При ковзанні шарів один відносно іншого відбувається перемелювання великих кристалічних зерен, тобто подрібнення кристалічної структури. Незначна частина вхідного потоку, найбільш віддалена від точки , внаслідок зменшення відносної швидкості при проходженні прес-форми, як це видно на рисунку 7.1б, захоплює значну частину її об’єму, яку ми називаємо «застійною зоною». Саме тут відносна швидкість від шару до шару змінюється особливо різко, саме в цій області подрібнення кристалічної структури відбувається найбільш інтенсивно.

Водночас необхідно відзначити, що виконання алгоритму (див. виконуваний файл Navier-Stokes_u,v,P.exe) вимагає порівняно великого часу обчислень, оскільки чисельний розв’язок будується для системи двох рівнянь (7.4)-(7.5) і не повною мірою враховує вплив вхідного і вихідного каналів штампу (див. рисунок 7.1). Отже для пришвидшення обчислень є сенс розглянути рівняння переносу вихору.